Application of Data Assimilation in Space Weather
-
摘要: 由太阳活动引起的耀斑和日冕物质抛射等短时间尺度变化的空间天气事件会影响并危害地球磁层、电离层、中高层大气、卫星运行安全以及人类健康,因此对这些空间天气事件的预测显得尤为重要。数据同化在稀疏观测和异步采集的情况下能够增加模型的预测能力,对模型变量进行自洽分析。在数值预报中引入数据同化方法,能够提高预测可信度。本文从数据同化方法的角度出发,主要分析了数据同化目前在大气、电离层、磁层、太阳及其他行星科学研究中的应用,并初步讨论了数据同化未来在空间天气方面的应用。Abstract: Space weather events caused by solar activities such as flares and Coronal Mass Ejections (CMEs) can affect the magnetosphere of the Earth, the middle and upper atmosphere, ionosphere, the safety of satellite operation and human health directly or indirectly. Therefore, the prediction of space weather events is particularly important. In the case of sparse observation and asynchronous sampling, data assimilation can increase the prediction ability of the model, self-consistent analysis of model variables can be carried out, and the introduction of data assimilation method in numerical prediction can improve the reliability of the prediction. This paper mainly introduces the application of data assimilation in the atmosphere, ionosphere, magnetosphere, the Sun and other planets from the perspective of data assimilation methods. The potential applications of data assimilation in space weather in the future are also discussed.
-
Key words:
- Data assimilation /
- Kalman filter /
- Space weather /
- Solar wind
-
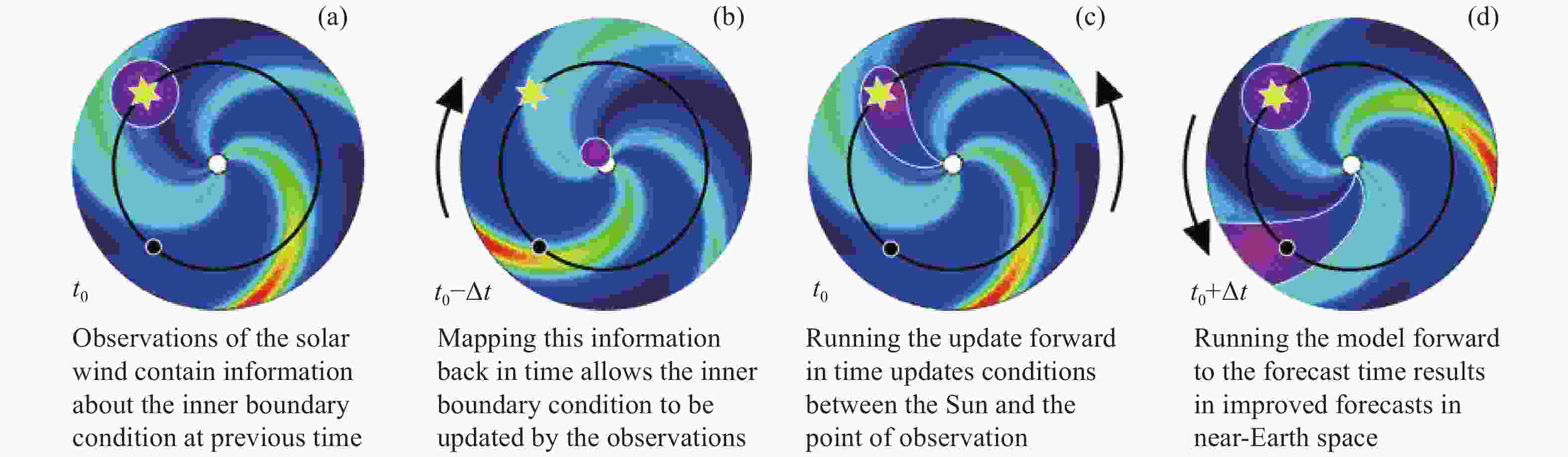
图 5 BRaVDA方案工作原理。内部边界(白色圆圈)使用来自地球轨道后方位置(黄星)的观测信息更新,更新后的模型条件(紫色区域)保留在模型域中,从而影响地球位置(黑色圆圈)的预测
Figure 5. A schematic of how the BRaVDA scheme works. The inner boundary (the white circle) is updated using information from observations from a position behind Earth in its orbit (the yellow star). The updated model conditions (the purple regions) persist in the model domain such that they impact forecasts at Earth’s location (the black circle)
表 1 数据同化模型
Table 1. Data assimilation models
同化模型 应用范围 全球同化电离层模型–有限带宽 中纬度到低纬度电离层 全球电离层测量同化–高斯马尔
可夫中纬度到低纬度电离层 全球同化电离层模型–四维变分 带驱动的中纬度到低纬度电离层 全球电离层测量同化–全物理 带驱动的中纬度到低纬度电离层
等离子体层中–低纬度电动力学–数据同化 带驱动的中纬度到低纬度电离层 电离层动力学和电动力学–数据
同化带驱动的高纬度电离层 全球热层模型–数据同化 全球热层模型数据同化 -
[1] 冯学尚. 空间天气学——21世纪的新兴学科[J]. 世界科技研究与发展, 2000, 22(2): 50-53 doi: 10.3969/j.issn.1006-6055.2000.02.012FENG Xueshang. Space weather——a new discipline of the 21 st century[J]. World Sci-Tech R & D, 2000, 22(2): 50-53 doi: 10.3969/j.issn.1006-6055.2000.02.012 [2] TALAGRAND O. Assimilation of observations, an introduction[J]. Journal of the Meteorological Society of Japan, 1997, 75(1B): 191-209 [3] DALEY R. Atmospheric Data Analysis[M]. Cambridge: Cambridge University Press, 1991: 191 [4] NATVIK L J, EVENSEN G. Assimilation of ocean colour data into a biochemical model of the North Atlantic: part 2. statistical analysis[J]. Journal of Marine Systems, 2003, 40/41: 155-169 doi: 10.1016/S0924-7963(03)00017-4 [5] LISAETER K A, ROSANOVA J, EVENSEN G. Assimilation of ice concentration in a coupled ice–ocean model, using the ensemble Kalman filter[J]. Ocean Dynamics, 2003, 53(4): 368-388 doi: 10.1007/s10236-003-0049-4 [6] NAEVDAL G, JOHNSEN L M, AANONSEN S I, et al. Reservoir monitoring and continuous model updating using ensemble Kalman filter[J]. SPE Journal, 2005, 10(1): 66-74 doi: 10.2118/84372-PA [7] ARGE C N, HENNEY C J, KOLLER J, et al. Air force Data Assimilative Photospheric flux Transport (ADAPT) model[J]. AIP Conference Proceedings, 2010, 1216(1): 343-346 [8] LANG M, OWENS M J. A variational approach to data assimilation in the solar wind[J]. Space Weather, 2019, 17(1): 59-83 doi: 10.1029/2018SW001857 [9] 李新, 小池俊雄, 程国栋. 一个基于模拟退火法的陆面数据同化算法[J]. 地球科学进展, 2003, 18(4): 632-636 doi: 10.3321/j.issn:1001-8166.2003.04.022LI Xin, Toshio K, CHENG Guodong. An algorithm for land data assimilation by using simulated annealing method[J]. Advance in Earth Sciences, 2003, 18(4): 632-636 doi: 10.3321/j.issn:1001-8166.2003.04.022 [10] 王跃山. 数据同化——它的缘起、含义和主要方法[J]. 海洋预报, 1999, 16(1): 11-20 doi: 10.11737/j.issn.1003-0239.1999.01.002WANG Yueshan. Data assimilation its cause, its meaning and main procedures[J]. Marine Forecasts, 1999, 16(1): 11-20 doi: 10.11737/j.issn.1003-0239.1999.01.002 [11] 马建文, 秦思娴. 数据同化算法研究现状综述[J]. 地球科学进展, 2012, 27(7): 747-757MA Jianwen, QIN Sixian. Recent advances and development of data assimilation algorithms[J]. Advances in Earth Sciences, 2012, 27(7): 747-757 [12] 李新, 摆玉龙. 顺序数据同化的Bayes滤波框架[J]. 地球科学进展, 2010, 25(5): 515-522LI Xin, BAI Yulong. A Bayesian filter framework for sequential data assimilation[J]. Advances in Earth Science, 2010, 25(5): 515-522 [13] HAYKIN S. Kalman Filtering and Neural Networks[M]. New York: John Wiley & Sons, Inc., 2001: 170-174 [14] EVENSEN G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics[J]. Journal of Geophysical Research, 1994, 99(C5): 10143-10162 doi: 10.1029/94JC00572 [15] BURGERS G, VAN LEEUWEN P J, EVENSEN G. Analysis scheme in the ensemble Kalman filter[J]. Monthly Weather Review, 1998, 126(6): 1719-1724 doi: 10.1175/1520-0493(1998)126<1719:ASITEK>2.0.CO;2 [16] KALMAN R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 1960, 82(1): 35-45 doi: 10.1115/1.3662552 [17] PERIÁÑEZ Á, REICH H, POTTHAST R. Optimal localization for ensemble Kalman filter systems[J]. Journal of the Meteorological Society of Japan, 2014, 92(6): 585-597 [18] LANG M, VAN LEEUWEN P J, BROWNE P. A systematic method of parameterisation estimation using data assimilation[J]. Tellus A: Dynamic Meteorology and Oceanography, 2016, 68(1): 29012 doi: 10.3402/tellusa.v68.29012 [19] TORRES G A. Algorithm 900: a discrete time Kalman filter package for large scale problems[J]. ACM Transactions on Mathematical Software, 2010, 37(1): 11 [20] HAMILL T M, WHITAKER J S, SNYDER C. Distance-dependent filtering of background error covariance estimates in an ensemble Kalman filter[J]. Monthly Weather Review, 2001, 129(11): 2776-2790 doi: 10.1175/1520-0493(2001)129<2776:DDFOBE>2.0.CO;2 [21] BARETTA J W, EBENHÖH W, RUARDIJ P. The European regional seas ecosystem model, a complex marine ecosystem model[J]. Netherlands Journal of Sea Research, 1995, 33(3/4): 233-246 [22] VAN LOON M, BUILTJES P J H, SEGERS A J. Data assimilation of ozone in the atmospheric transport chemistry model LOTOS[J]. Environmental Modelling & Software, 2000, 15(6/7): 603-609 [23] BROWNE P A, VAN LEEUWEN P J. Twin experiments with the equivalent weights particle filter and HadCM3[J]. Quarterly Journal of the Royal Meteorological Society, 2015, 141(693): 3399-3414 doi: 10.1002/qj.2621 [24] GYÖRGY K, KELEMEN A, DÁVID L. Unscented kalman filters and particle filter methods for nonlinear state estimation[J]. Procedia Technology, 2014, 12: 65-74 doi: 10.1016/j.protcy.2013.12.457 [25] 胡士强, 敬忠良. 粒子滤波算法综述[J]. 控制与决策, 2005, 20(4): 361-365,371 doi: 10.3321/j.issn:1001-0920.2005.04.001HU Shiqiang, JING Zhongliang. Overview of particle filter algorithm[J]. Control and Decision, 2005, 20(4): 361-365,371 doi: 10.3321/j.issn:1001-0920.2005.04.001 [26] COURTIER P, THÉPAUT J N, HOLLINGSWORTH A. A strategy for operational implementation of 4 D-Var, using an incremental approach[J]. Quarterly Journal of the Royal Meteorological Society, 1994, 120(519): 1367-1387 doi: 10.1002/qj.49712051912 [27] COURTIER P, ANDERSSON E, HECKLEY W, et al. The ECMWF implementation of three-dimensional variational assimilation (3 D-Var). I: formulation[J]. Quarterly Journal of the Royal Meteorological Society, 1998, 124(550): 1783-1807 [28] LEWIS J M, DERBER J C. The use of adjoint equations to solve a variational adjustment problem with advective constraints[J]. Tellus A: Dynamic Meteorology and Oceanography, 1985, 37(4): 309-322 doi: 10.3402/tellusa.v37i4.11675 [29] LE DIMET F X, TALAGRAND O. Variational algorithms for analysis and assimilation of meteorological observations: theoretical aspects[J]. Tellus A: Dynamic Meteorology and Oceanography, 1986, 38(2): 97-110 doi: 10.3402/tellusa.v38i2.11706 [30] RABIER F. Overview of global data assimilation developments in numerical weather-prediction centres[J]. Quarterly Journal of the Royal Meteorological Society, 2005, 131(613): 3215-3233 doi: 10.1256/qj.05.129 [31] HUNT B R, KOSTELICH E J, SZUNYOGH I. Efficient data assimilation for spatiotemporal chaos: a local ensemble transform Kalman filter[J]. Physica D: Nonlinear Phenomena, 2007, 230(1/2): 112-126 [32] BISHOP C H, ETHERTON B J, MAJUMDAR S J. Adaptive sampling with the ensemble transform Kalman filter. Part I: theoretical aspects[J]. Monthly Weather Review, 2001, 129(3): 420-436 doi: 10.1175/1520-0493(2001)129<0420:ASWTET>2.0.CO;2 [33] LANG M, BROWNE P, VAN LEEUWEN P J, et al. Data assimilation in the solar wind: challenges and first results[J]. Space Weather, 2017, 15(11): 1490-1510 doi: 10.1002/2017SW001681 [34] BROWNE P A, WILSON S. A simple method for integrating a complex model into an ensemble data assimilation system using MPI[J]. Environmental Modelling & Software, 2015, 68: 122-128 [35] ZHU M B, VAN LEEUWEN P J, AMEZCUA J. Implicit equal-weights particle filter[J]. Quarterly Journal of the Royal Meteorological Society, 2016, 142(698): 1904-1919 doi: 10.1002/qj.2784 [36] ANDERSON J, HOAR T, RAEDER K, et al. The data assimilation research testbed: a community facility[J]. Bulletin of the American Meteorological Society, 2009, 90(9): 1283-1296 doi: 10.1175/2009BAMS2618.1 [37] NERGER L, HILLER W, SCHRÖTER J. PDAF-the parallel data assimilation framework: experiences with Kalman filtering[M]//ZWIEFLHOFER W, MOZDZYNSKI G. Use of High Performance Computing in Meteorology. Singapore: World Scientific, 2005: 63-83 [38] VAN VELZEN N, VERLAAN M. Costa a problem solving environment for data assimilation applied for hydrodynamical modelling[J]. Meteorologische Zeitschrift, 2007, 16(6): 777-793 doi: 10.1127/0941-2948/2007/0241 [39] WEERTS A H, EL SERAFY G Y, HUMMEL S, et al. Application of generic Data Assimilation Tools (DATools) for flood forecasting purposes[J]. Computers & Geosciences, 2010, 36(4): 453-463 [40] RIDLER M E, VAN VELZEN N, HUMMEL S, et al. Data assimilation framework: linking an Open DAta assimilation library (OpenDA) to a widely adopted Model Interface (OpenMI)[J]. Environmental Modelling & Software, 2014, 57: 76-89 [41] SMEDSTAD O M, O'BRIEN J J. Variational data assimilation and parameter estimation in an equatorial Pacific ocean model[J]. Progress in Oceanography, 1991, 26(2): 179-241 doi: 10.1016/0079-6611(91)90002-4 [42] OTT E, HUNT B R, SZUNYOGH I, et al. A local ensemble Kalman filter for atmospheric data assimilation[J]. Tellus A: Dynamic Meteorology and Oceanography, 2004, 56(5): 415-428 doi: 10.3402/tellusa.v56i5.14462 [43] SMITH P J, DANCE S L, BAINES M J, et al. Variational data assimilation for parameter estimation: application to a simple morphodynamic model[J]. Ocean Dynamics, 2009, 59(5): 697-708 doi: 10.1007/s10236-009-0205-6 [44] MIYOSHI T, SATO Y, KADOWAKI T. Ensemble Kalman filter and 4 D-Var intercomparison with the Japanese operational global analysis and prediction system[J]. Monthly Weather Review, 2010, 138(7): 2846-2866 doi: 10.1175/2010MWR3209.1 [45] 林行, 高山红, 黄容. 大气数据同化方法的研究与应用进展[J]. 山东气象, 2004, 24(4): 16-18LIN Hang, GAO Shanhong, HUANG Rong. The developments and applications of atmosphereic data assimilation[J]. Journal of Shandong Meteorology, 2004, 24(4): 16-18 [46] DURAZO J A, KOSTELICH E J, MAHALOV A. Local ensemble transform Kalman filter for ionospheric data assimilation: observation influence analysis during a geomagnetic storm event[J]. Journal of Geophysical Research, 2017, 122(9): 9652-9669 doi: 10.1002/2017JA024274 [47] HSU C T, MATSUO T, LIU J Y. Impact of assimilating the FORMOSAT-3/COSMIC and FORMOSAT-7/COSMIC-2 RO data on the midlatitude and low-latitude ionospheric specification[J]. Earth and Space Science, 2018, 5(12): 875-890 doi: 10.1029/2018EA000447 [48] 阿尔察, 刘四清, 黄文耿, 等. 中国电离层TEC同化现报系统[J]. 地球物理学报, 2018, 61(6): 2186-2197 doi: 10.6038/cjg2018L0349A Ercha, LIU Siqing, HUANG Wengeng, et al. Ionospheric TEC data assimilation and now-casting system over China[J]. Chinese Journal of Geophysics, 2018, 61(6): 2186-2197 doi: 10.6038/cjg2018L0349 [49] GARDNER L C, SCHUNK R W, SCHERLIESS L, et al. Modeling the midlatitude ionosphere storm-enhanced density distribution with a data assimilation model[J]. Space Weather, 2018, 16(10): 1539-1548 doi: 10.1029/2018SW001882 [50] SCHUNK R W, SCHERLIESS L, SOJKA J J, et al. Global Assimilation of Ionospheric Measurements (GAIM)[J]. Radio Science, 2016, 39(1): RS1S02 [51] SCHUNK R W. A mathematical model of the middle and high latitude ionosphere[J]. Pure and Applied Geophysics, 1988, 127(2/3): 255-303 [52] SCHUNK R W, SCHERLIESS L, ECCLES V, et al. Ensemble modeling with data assimilation models: a new strategy for space weather specifications, forecasts, and science[J]. Space Weather, 2014, 12(3): 123-126 doi: 10.1002/2014SW001050 [53] QIAN L, BURNS A, EMERY B A, et al. The NCAR TIE-GCM: a community model of the coupled thermosphere/ionosphere system[M]//HUBA J, SCHUNK R, KHAZANOV G. Modeling the Ionosphere-Thermosphere System. Washington: John Wiley & Sons, 2014: 73-83 [54] LEE I T, MATSUO T, RICHMOND A D, et al. Assimilation of FORMOSAT-3/COSMIC electron density profiles into a coupled thermosphere/ionosphere model using ensemble Kalman filtering[J]. Journal of Geophysical Research, 2012, 117(A10): A10318 [55] 何建辉, 乐新安. 基于热层电离层耦合数据同化的热层参量估计[J]. 地球物理学报, 2020, 63(7): 2497-2505 doi: 10.6038/cjg2020N0267HE Jianhui, YUE Xin’an. The estimation of thermosphere state variables based on coupled thermosphere and ionosphere data assimilation[J]. Chinese Journal of Geophysics, 2020, 63(7): 2497-2505 doi: 10.6038/cjg2020N0267 [56] MANNUCCI A J, WILSON B D, YUAN D N, et al. A global mapping technique for GPS-derived ionospheric total electron content measurements[J]. Radio Science, 1998, 33(3): 565-582 doi: 10.1029/97RS02707 [57] HE J H, YUE X A, WANG W B, et al. EnKF ionosphere and thermosphere data assimilation algorithm through a sparse matrix method[J]. Journal of Geophysical Research, 2019, 124(8): 7356-7365 doi: 10.1029/2019JA026554 [58] LIU L B, WAN W X. Recent ionospheric investigations in China (2018-2019)[J]. Earth and Planetary Physics, 2020, 4(3): 179-205 doi: 10.26464/epp2020028 [59] ELVIDGE S, ANGLING M J. Using the local ensemble transform Kalman filter for upper atmospheric modelling[J]. Journal of Space Weather and Space Climate, 2019, 9: A30 doi: 10.1051/swsc/2019018 [60] GODINEZ H C, KOLLER J. Localized adaptive inflation in ensemble data assimilation for a radiation belt model[J]. Space Weather, 2016, 10(8): S08001 [61] PODLADCHIKOVA T V, SHPRITS Y Y, KONDRASHOV D, et al. Noise statistics identification for Kalman filtering of the electron radiation belt observations I: model errors[J]. Journal of Geophysical Research, 2014, 119(7): 5700-5724 doi: 10.1002/2014JA019897 [62] GARNER T W, WOLF R A, SPIRO R W, et al. First attempt at assimilating data to constrain a magnetospheric model[J]. Journal of Geophysical Research, 1999, 104(A11): 25145-25152 doi: 10.1029/1999JA900274 [63] JORGENSEN A M, OBER D, KOLLER J, et al. Specification of the Earth's plasmasphere with data assimilation[J]. Advances in Space Research, 2011, 47(12): 2152-2161 doi: 10.1016/j.asr.2010.06.013 [64] OBER D M, HORWITZ J L, GALLAGHER D L. Formation of density troughs embedded in the outer plasmasphere by subauroral ion drift events[J]. Journal of Geophysical Research, 1997, 102(A7): 14595-14602 doi: 10.1029/97JA01046 [65] SCHRIJVER C J, DEROSA M L. Photospheric and heliospheric magnetic fields[J]. Solar Physics, 2003, 212(1): 165-200 doi: 10.1023/A:1022908504100 [66] DIKPATI M, ANDERSON J L, MITRA D. Ensemble Kalman filter data assimilation in a Babcock-Leighton solar dynamo model: an observation system simulation experiment for reconstructing meridional flow speed[J]. Geophysical Research Letters, 2014, 41(15): 5361-5369 doi: 10.1002/2014GL061077 [67] JOUVE L, BRUN A S, TALAGRAND O. Assimilating data into an αΩ dynamo model of the sun: a variational approach[J]. The Astrophysical Journal, 2011, 735(1): 31 doi: 10.1088/0004-637X/735/1/31 [68] SVEDIN A, CUÉLLAR M C, BRANDENBURG A. Data assimilation for stratified convection[J]. Monthly Notices of the Royal Astronomical Society, 2013, 433(3): 2278-2285 doi: 10.1093/mnras/stt891 [69] WORDEN J, HARVEY J. An evolving synoptic magnetic flux map and implications for the distribution of photospheric magnetic flux[J]. Solar Physics, 2000, 195(2): 247-268 doi: 10.1023/A:1005272502885 [70] HICKMANN K S, GODINEZ H C, HENNEY C J, et al. Data assimilation in the ADAPT photospheric flux transport model[J]. Solar Physics, 2015, 290(4): 1105-1118 doi: 10.1007/s11207-015-0666-3 [71] ARGE C N, HENNEY C J, HERNANDEZ I G, et al. Modeling the corona and solar wind using ADAPT maps that include far-side observations[J]. AIP Conference Proceedings, 2013, 1539(1): 11-14 [72] JING L, ULRICH R K. Long-term measurements of sunspot magnetic tilt angles[J]. The Astrophysical Journal, 2012, 758(2): 115 doi: 10.1088/0004-637X/758/2/115 [73] WANG Y M, SHEELEY JR N R. On potential field models of the solar corona[J]. Astrophysical Journal, 1992, 392: 310-319 doi: 10.1086/171430 [74] SCHATTEN K H, WILCOX J M, NESS N F. A model of interplanetary and coronal magnetic fields[J]. Solar Physics, 1969, 6(3): 442-455 doi: 10.1007/BF00146478 [75] SCHATTEN K H. Current sheet magnetic model for the solar corona[J]. Cosmic Electrodynamics, 1971, 2: 232-245 [76] ARGE C N, HENNEY C J, KOLLER J, et al. Improving data drivers for coronal and solar wind models[C]//Proceedings of the 5th International Conference of Numerical Modeling of Space Plasma Flows. Francisco: Astronomical Society of the Pacific, 2011 [77] HICKMANN K S, GODINEZ H C, HENNEY C J, et al. Scale-dependent data assimilation of solar photospheric magnetic field[J]. IFAC-PapersOnLine, 2016, 49(18): 193-198 doi: 10.1016/j.ifacol.2016.10.162 [78] RILEY P, LIONELLO R. Mapping solar wind streams from the Sun to 1 AU: a comparison of techniques[J]. Solar Physics, 2011, 270(2): 575-592 doi: 10.1007/s11207-011-9766-x [79] LANG M, WITHERINGTON J, TURNER H, et al. Improving solar wind forecasting using data assimilation[J]. Space Weather, 2021, 19(7): e2020SW002698 [80] OWENS M, LANG M, BARNARD L, et al. A computationally efficient, time-dependent model of the solar wind for use as a surrogate to three-dimensional numerical magnetohydrodynamic simulations[J]. Solar Physics, 2020, 295(3): 43 doi: 10.1007/s11207-020-01605-3 [81] MERKA J, MERKOVA D, ODSTRCIL D. A step toward data assimilation in solar wind research[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2007, 69(1/2): 170-178 [82] LEE C O, LUHMANN J G, ODSTRCIL D, et al. The solar wind at 1 AU during the declining phase of solar cycle 23: comparison of 3 D numerical model results with observations[J]. Solar Physics, 2009, 254(1): 155-183 doi: 10.1007/s11207-008-9280-y [83] INNOCENTI M E, LAPENTA G, VRŠNAK B, et al. Improved forecasts of solar wind parameters using the Kalman filter[J]. Space Weather, 2011, 9(10): S10005 [84] VRŠNAK B, TEMMER M, VERONIG A M. Coronal holes and solar wind high-speed streams: I. Forecasting the solar wind parameters[J]. Solar Physics, 2007, 240(2): 315-330 doi: 10.1007/s11207-007-0285-8 [85] MEADORS G D, JONES S I, HICKMANN K S, et al. Data assimilative optimization of WSA source surface and interface radii using particle filtering[J]. Space Weather, 2020, 18(5): e2020SW002464 [86] BOCQUET M, PIRES C A, WU L. Beyond Gaussian statistical modeling in geophysical data assimilation[J]. Monthly Weather Review, 2010, 138(8): 2997-3023 doi: 10.1175/2010MWR3164.1 [87] LEWIS S R. Data assimilation for other planets[M]//LAHOZ W, KHATTATOV B, MENARD R. Data Assimilation: Making Sense of Observations. Berlin: Springer, 2010 [88] LEWIS S R, COLLINS M, READ P L. Data assimilation with a Martian atmospheric GCM: an example using thermal data[J]. Advances in Space Research, 1997, 19(8): 1267-1270 doi: 10.1016/S0273-1177(97)00280-9 [89] KASS D M. Change in the Martian Atmosphere[D]. California: California Institute of Technology, 1999 [90] FORGET F, HOURDIN F, FOURNIER R, et al. Improved general circulation models of the Martian atmosphere from the surface to above 80 km[J]. Journal of Geophysical Research, 1999, 104(E10): 24155-24175 doi: 10.1029/1999JE001025 [91] MONTABONE L, LEWIS S R, READ P L, et al. Validation of martian meteorological data assimilation for MGS/TES using radio occultation measurements[J]. Icarus, 2006, 185(1): 113-132 doi: 10.1016/j.icarus.2006.07.012 [92] FENG X S. Current status of MHD simulations for space weather[M]//FENG X S. Magnetohydrodynamic Modeling of the Solar Corona and Heliosphere. Singapore: Springer, 2020 [93] 摆玉龙, 李新, 韩旭军. 陆面数据同化系统误差问题研究综述[J]. 地球科学进展, 2011, 26(8): 795-804BAI Yulong, LI Xin, HAN Xujun. A review of error problems for land data assimilation systems[J]. Advances in Earth Sciences, 2011, 26(8): 795-804 [94] ZUPANSKI D, ZUPANSKI M. Model error estimation employing an ensemble data assimilation approach[J]. Monthly Weather Review, 2006, 134(5): 1337-1354 doi: 10.1175/MWR3125.1 [95] TRÉMOLET Y. Model-error estimation in 4 D-Var[J]. Quarterly Journal of the Royal Meteorological Society, 2007, 133(626): 1267-1280 doi: 10.1002/qj.94 [96] CARRASSI A, VANNITSEM S, NICOLIS C. Model error and sequential data assimilation: a deterministic formulation[J]. Quarterly Journal of the Royal Meteorological Society, 2008, 134(634): 1297-1313 doi: 10.1002/qj.284 [97] 杨子才. 行星际背景太阳风的三维磁流体力学数值模拟[D]. 北京: 中国科学院大学(中国科学院国家空间科学中心), 2018YANG Zicai. Three Dimensional MHD Numerical Simulation of the Interplanetary Background Solar Wind[D]. Beijing: University of Chinese Academy of Sciences (National Space Science Center Chinese Academy of Sciences), 2018 -
-





 下载:
下载: