Research on the Spatio-temporal Coding Scheme for the Dynamic Earth’s Magnetosphere
-
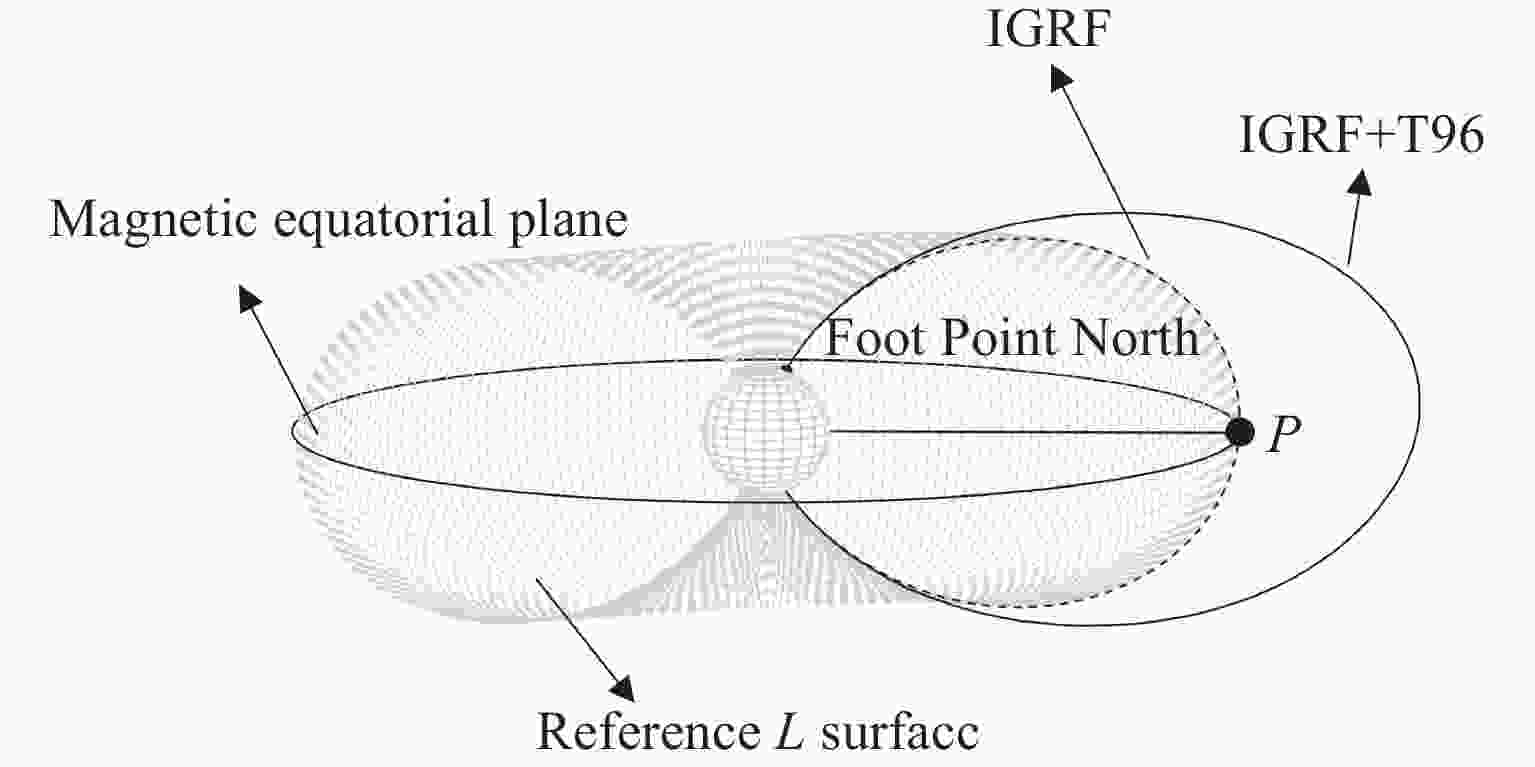
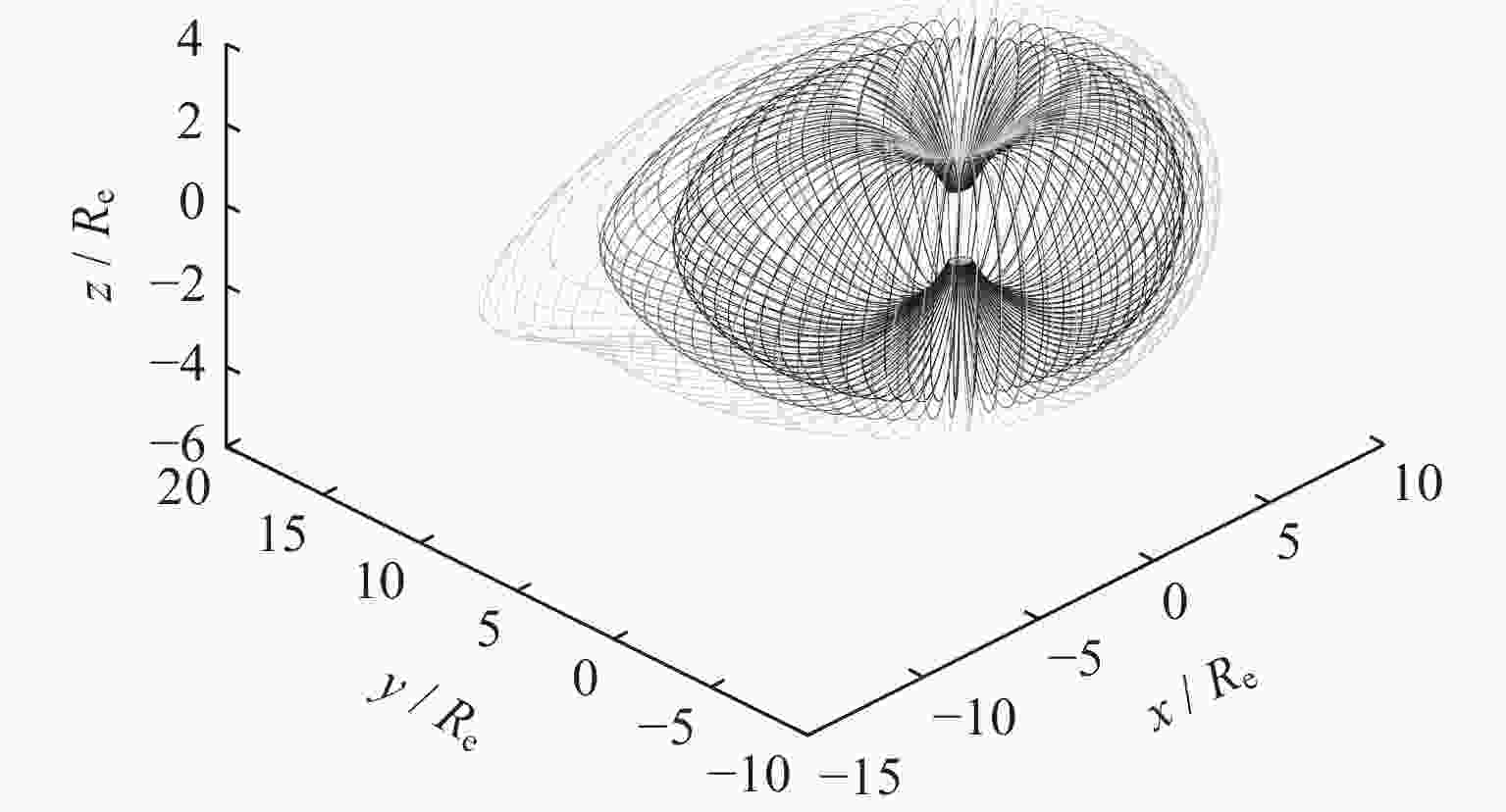
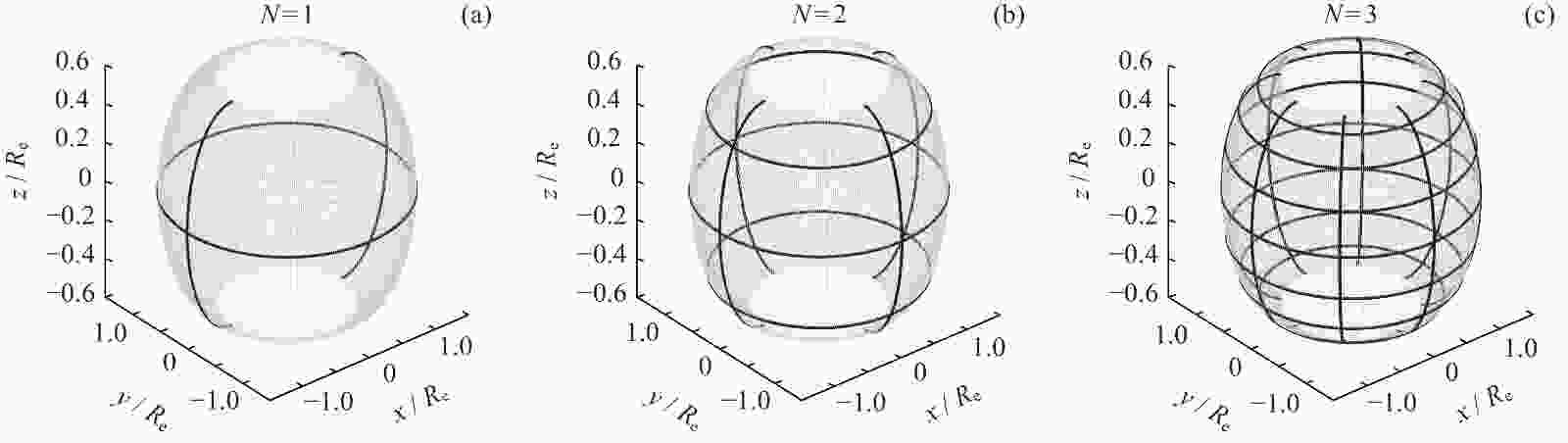
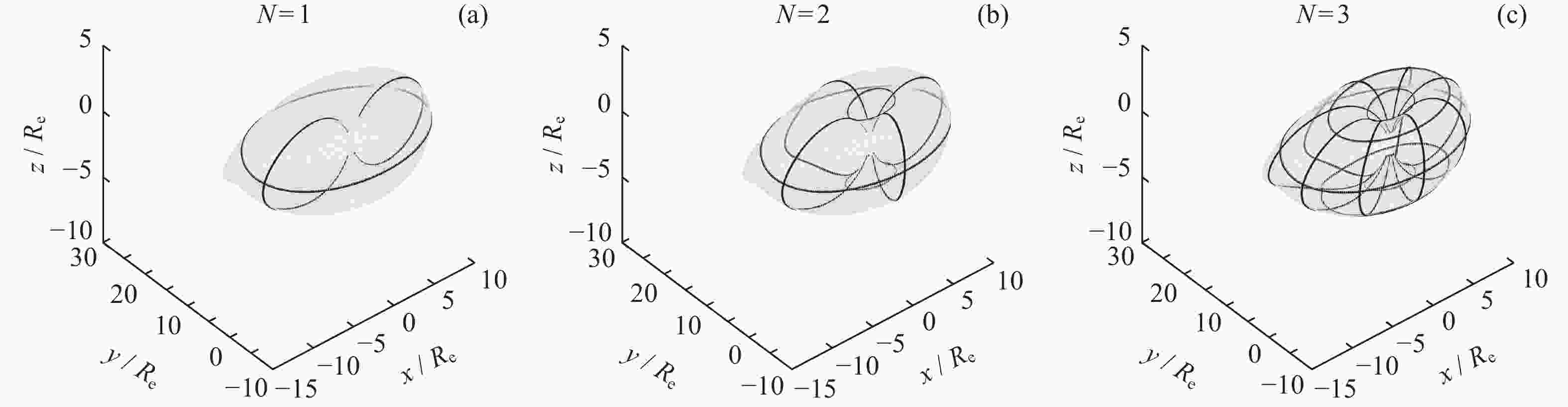
摘要: 动态地球磁层时空剖分模型借鉴了广泛应用于地学大数据的地球格网模型思想,实现了面向地球磁层的动态、非规则化物理空间的多层级剖分,且剖分格网形变稳定,可以实现一定范围内地球磁层时空特性的形式化。在此基础上,对剖分得到的时空格网进行编码表达,以便于计算机存储和处理,这是构建地球磁层大规模观测数据统一管理基础时空框架的另一个关键问题。由于地球磁层特殊的时空特性,经典、单一思路的地学编码方案较难完整地反映格网间的时空关系,因此难以支持格网间的基础时空关系计算。本文融合了整数坐标编码与Morton曲线编码的基本思路,实现了对漂移壳剖分格网的高效编码方案设计,完成了动态地球磁层的时空框架构建,从而为地磁数据的高效组织和处理奠定了基础。实验证明,本文提出的编码方案编码效率较高,且可以支持高效的相邻关系计算,为动态地球磁层多源、多层级、异构的大规模观测数据的组织与计算提供了一种解决方案。Abstract: The spatio-temporal subdivision model for the dynamic Earth’s magnetosphere is proposed to realize the multi-layered subdivision for the dynamic and irregular physical space of the magnetosphere drawing on the idea of the global discrete grids for the geoscience data. The distortion of the grids can be convergent within a certain number of subdivision times. Therefore, the subdivision model can be taken as a formalization for the spatio-temporal characteristics of the Earth’s magnetosphere in a certain range. On this basis, encoding and expressing the spatio-temporal grids obtained by subdivision for computer storage and processing is another key problem in constructing the basic spatio-temporal framework for the organization and management of large-scale observation data of the Earth’s magnetosphere. Due to the specific spatio-temporal characteristics, the classical geoscience coding schemes have trouble in fully reflecting the spatio-temporal relations between the grids. Therefore, it is difficult to support the basic spatio-temporal computing between the grids. In this paper, an efficient coding scheme is designed for the drift shell subdivision grids combining the basic ideas of the integral coordinate coding and the Morton coding schemes. On this basis, the spatio-temporal framework for the dynamic Earth’s magnetosphere is constructed which lays the foundation for the efficient organization and processing of geomagnetic data. The experiments carried out show that, the coding efficiency of the scheme is relatively high and it can support efficient neighbor relationship calculation. It provides a solution for the organization and computing of the multi-source, multi-layered, heterogeneous and large-scale observation data of the dynamic Earth’s magnetosphere.
-
表 1 集群环境
Table 1. Cluster environment
硬件环境 软件环境 CPU RAM(GB) HDD(GB) OS Matlab 6核 16 512 Windows 10 2018 表 2 偶极磁场区域编码效率
Table 2. Encoding efficiency in the dipole field
$ N $ 编码效率 /s–1 Morton曲线编码 整数坐标编码 6 51003.00 44678.60 7 127832.2 125360.6 8 196152.1 181619.7 9 204222.4 193187.9 10 198420.7 199054.0 11 96747.54 96548.7 12 153574.2 197650.5 表 3 非偶极磁场区域平均编码效率
Table 3. Mean encoding efficiency in the non-dipole field
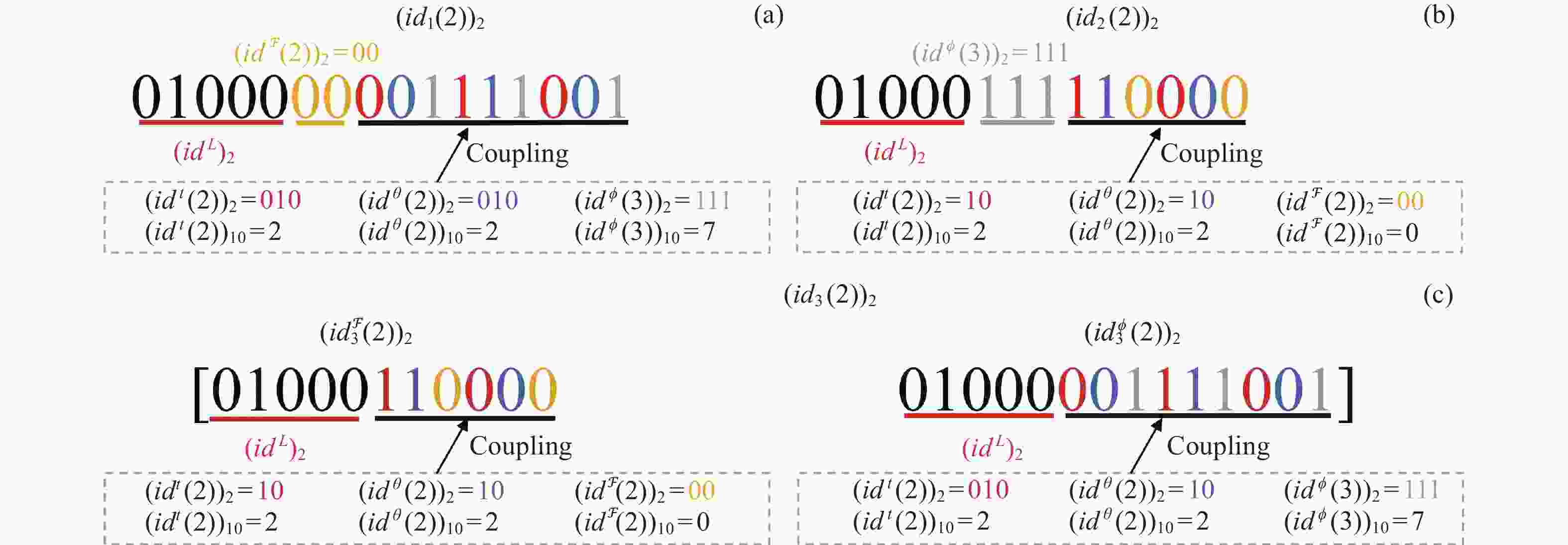
$ N $ Morton编码 整数坐标编码 编码效率/s–1 $ {\left(i{d}_{1}\left(N\right)\right)}_{2} $ $ {\left(i{d}_{2}\left(N\right)\right)}_{2} $ $ {\left(i{d}_{3}\left(N\right)\right)}_{2} $ 6 25451.59 23660.08 16319.32 17338.22 17739.12 7 41171.38 38646.57 34454.50 33378.99 35573.91 8 40192.71 35873.30 40000.48 39031.26 38787.78 9 29902.72 29887.52 34048.59 31543.25 32049.48 10 19640.26 20587.83 21000.26 21718.52 21641.38 11 10946.56 11460.08 11741.83 12218.11 12243.30 12 4930.94 5760.11 5042.20 4946.66 4896.83 表 4 剖分格网的基础相邻关系
Table 4. Basic adjacency of the grids
邻居类型 纬度维 磁力线维 经度维 上邻居(T) $ {\left(i{d}_{{\rm{T}}}^{\theta }\left(N\right)\right)}_{10}={\left(i{d}^{\theta }\left(N\right)\right)}_{10}+1 $ $ {\left(i{d}_{{\rm{T}}}^{\mathcal{F}}\left(N\right)\right)}_{10}={\left(i{d}^{\mathcal{F}}\left(N\right)\right)}_{10} $ - 下邻居(B) $ {\left(i{d}_{{\rm{B}}}^{\theta }\left(N\right)\right)}_{10}={\left(i{d}^{\theta }\left(N\right)\right)}_{10}-1 $ $ {\left(i{d}_{{\rm{B}}}^{\mathcal{F}}\left(N\right)\right)}_{10}={\left(i{d}^{\mathcal{F}}\left(N\right)\right)}_{10} $ - 左邻居(L) $ {\left(i{d}_{{\rm{L}}}^{\theta }\left(N\right)\right)}_{10}={\left(i{d}^{\theta }\left(N\right)\right)}_{10} $ - $\begin{array}{l}{\left( {id_{\rm{L} }^\phi \left( { {N_\phi } } \right)} \right)_{10} }\\ \quad = \left\{ {\begin{array}{*{20}{l} }{ {2^{ {N_\phi } } } - 1,if{ {\left( {i{d^\phi }\left( { {N_\phi } } \right)} \right)}_{10} } = 0}\\{ { {\left( {i{d^\phi }\left( { {N_\phi } } \right)} \right)}_{10} } - 1,{\rm{otherwise} } }\end{array} } \right.\end{array}$ 右邻居(R) $ {\left(i{d}_{{\rm{R}}}^{\theta }\left(N\right)\right)}_{10}={\left(i{d}^{\theta }\left(N\right)\right)}_{10} $ - $\begin{array}{l}{\left( {id_{\rm{R} }^\phi \left( { {N_\phi } } \right)} \right)_{10} }\\ \quad = \left\{ {\begin{array}{*{20}{l} }{0,if{ {\left( {i{d^\phi }\left( { {N_\phi } } \right)} \right)}_{10} } = {2^{ {N_\phi } } } - 1}\\{ { {\left( {i{d^\phi }\left( { {N_\phi } } \right)} \right)}_{10} } + 1,{\rm{otherwise} } }\end{array} } \right.\end{array}$ 表 5 偶极磁场区域格网基础相邻关系计算效率对比
Table 5. Efficiency comparison of the basic adjacency of the grids in the dipole field
平均计算效率/s–1 T B L R TL TR BL BR Morton曲线编码 118884.9 114516.1 122907.5 119481.5 126159.1 124904.8 121647.1 126411.1 整数坐标编码 140970.2 139378.6 133924.4 130746.3 131747.1 128346.6 130744.6 129471.6 表 6 非偶极磁场区域格网基础相邻关系计算效率对比
Table 6. Efficiency comparison of the basic adjacency of the grids in the non-dipole field
平均计算效率/s–1 T B L R TL TR BL BR $ {\left(i{d}_{1}\left(N\right)\right)}_{2} $ 45.273 29.391 8.776 8.776 3.142 3.239 3.434 3.326 $ {\left(i{d}_{2}\left(N\right)\right)}_{2} $ 23.411 22.775 8.310 6.149 2.636 2.610 2.809 2.161 $ {\left(i{d}_{3}\left(N\right)\right)}_{2} $ 89.412 89.711 90.156 89.363 89.276 90.351 89.530 89.731 -
[1] KING T, THIEMAN J, ROBERTS A D. SPASE 2.0: a standard data model for space physics[J]. Earth Science Informatics, 2010, 3(1/2): 67-73 [2] 徐文耀. 地磁与空间物理资料的组织和相关坐标系[J]. 地球物理学进展, 2006, 21(4): 1043-1060 doi: 10.3969/j.issn.1004-2903.2006.04.002XU Wenyao. Data organization in geomagnetism and space physics and relevant coordinate systems[J]. Progress in Geophysics, 2006, 21(4): 1043-1060 doi: 10.3969/j.issn.1004-2903.2006.04.002 [3] 李志强, 程承旗, 李爽. 基于GeoSOT-3D的空间对象快速可视化与实验分析[J]. 地球信息科学学报, 2015, 17(7): 810-815LI Zhiqiang, CHENG Chengqi, LI Shuang. Research on spatial objects fast visualization based on GeoSOT-3D[J]. Journal of Geo-Information Science, 2015, 17(7): 810-815 [4] 吴立新, 余接情. 基于球体退化八叉树的全球三维网格与变形特征[J]. 地理与地理信息科学, 2009, 25(1): 1-4WU Lixin, YU Jieqing. Global 3D-grid based on sphere degenerated octree and its distortion features[J]. Geography and Geo-Information Science, 2009, 25(1): 1-4 [5] 康栋贺, 邹自明, 胡晓彦, 等. 支持时空耦合计算的HTM-ST日地空间系统数据组织模型[J]. 地球信息科学学报, 2017, 19(6): 735-743 doi: 10.3969/j.issn.1560-8999.2017.06.002KANG Donghe, ZOU Ziming, HU Xiaoyan, et al. HTM-ST: A data model supporting spatio-temporal coupled computation for solar-terrestrial system[J]. Journal of Geo-Information Science, 2017, 19(6): 735-743 doi: 10.3969/j.issn.1560-8999.2017.06.002 [6] 赵学胜, 贲进, 孙文彬, 等. 地球剖分格网研究进展综述[J]. 测绘学报, 2016, 45(S1): 1-14 doi: 10.11947/j.AGCS.2016.F001ZHAO Xuesheng, BEN Jin, SUN Wenbin, et al. Overview of the research progress in the Earth tessellation grid[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(S1): 1-14 doi: 10.11947/j.AGCS.2016.F001 [7] 曹雪峰. 地球圈层空间网格理论与算法研究[D]. 郑州: 解放军信息工程大学, 2012CAO Xuefeng. Research on Earth sphere shell space grid theory and algorithms[D]. Zhengzhou: PLA Information Engineering University, 2012 [8] MCILWAIN C E. Magnetic coordinates[J]. Space Science Reviews, 1966, 5(5): 585-598 doi: 10.1007/BF00167327 [9] FUNG S F, TAN L C. An alternative drift shell parameter for modeling trapped particles[J]. Radiation Measurements, 1999, 30(5): 609-615 doi: 10.1016/S1350-4487(99)00243-7 [10] 钟佳, 邹自明. 地磁偶极子场磁力线疏密可视化算法[J]. 地球物理学进展, 2014, 29(6): 2614-2619 doi: 10.6038/pg20140622ZHONG Jia, ZOU Ziming. The algorithm of density visualization of magnetic flux lines based on geo-magnetic dipole field[J]. Progress in Geophysics, 2014, 29(6): 2614-2619 doi: 10.6038/pg20140622 [11] THÉBAULT E, FINLAY C C, BEGGAN C D, et al. International geomagnetic reference field: the 12 th generation[J]. Earth, Planets and Space, 2015, 67(1): 79 doi: 10.1186/s40623-015-0228-9 [12] FORSYTHE G E. Numerical methods for high-speed computers: a survey[C]//Papers presented at the March 3-5, 1959, Western Joint Computer Conference. San Francisco: ACM, 1959 [13] TSYGANENKO N A. Modeling the Earth's magnetospheric magnetic field confined within a realistic magnetopause[J]. Journal of Geophysical Research: Space Physics, 1995, 100(A4): 5599-5612 doi: 10.1029/94JA03193 -
-







 下载:
下载: