基于最小轨道交叉距离的小行星顺访探测目标预筛选方法
doi: 10.11728/cjss2022.05.210906097 cstr: 32142.14.cjss2022.05.210906097
Target Pre-screening Method for Asteroid Exploration Based on Minimum Orbital Intersection Distance
-
摘要: 小行星探测有助于研究太阳系演化等重要科学问题,在深空探测任务转移途中实施小行星顺访探测可增加科学研究回报。直接通过轨道递推筛选小行星探测目标计算量大、效率低,针对该问题提出了基于最小轨道交叉距离的目标预筛选方法。在推导出适用于计算双曲线轨道的最小轨道交叉距离公式后,将此理论应用到小行星顺访探测目标筛选中。首先基于探测器与小行星轨道的形状、空间位置计算二者轨道在空间中的几何最近距离,预筛选出可能满足接近距离标准的小行星目标;然后基于轨道递推模型,筛选出真实最近距离小于可接近标准的目标小行星。仿真结果显示,基于最小轨道交叉距离的预筛选方法可有效减少计算量,降低计算时间,提高小行星顺访目标筛选的效率。Abstract: Asteroid exploration helps to study important scientific issues such as the evolution of the solar system, and the implementation of asteroid exploration during the transfer of deep space missions can increase scientific returns. Aiming at the problem of large calculation amount and low efficiency in the primary selection of asteroid exploration targets directly through orbit recursion, a target pre-screening method based on the minimum orbital intersection distance is proposed. After the formula for calculating minimum orbital intersection distance for hyperbolic orbit is derived, the theory is applied to the screening of asteroid exploration targets. Firstly, based on the shape and spatial position of the orbits of the probe and the asteroids, the geometric closest distances between their orbits are calculated, and the asteroid targets that may meet the approach distance criteria are pre-screened. Then, based on the orbit recursive model, the target asteroids whose real closest distance to the probe is less than approach distance criteria are selected. The simulation results show that this pre-screening method based on the minimum orbital intersection distance can effectively reduce the amount of calculation and reduce the calculation time, thus improving the efficiency of asteroid target determination.
-
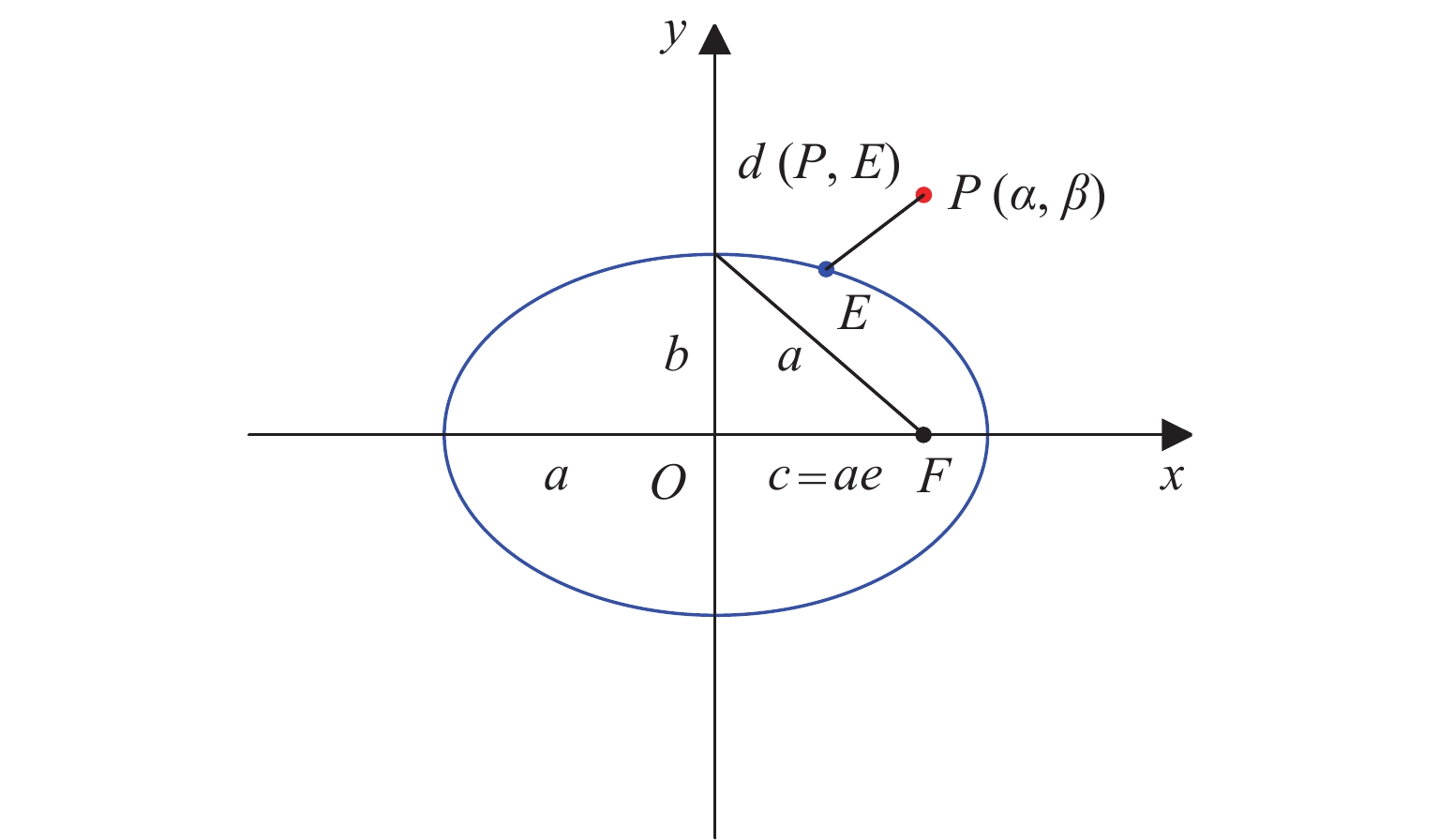
表 1 平面内一点与椭圆之间最近距离的封闭解情况
Table 1. Cases of minimum distance between an ellipse and a coplanar point with closed-form solution
$e = 0$ $0 < e < 1$ $\alpha = 0,\;\;\beta = 0$ $\alpha = 0,\;\;\beta > 0$ $\alpha > 0,\;\;\beta = 0$ $\alpha > {e^2}a$ $\alpha \leqslant {e^2}a$ ${u^{E'}}$ ${{\rm{arctan}} }\dfrac{\beta }{\alpha }$ $ \pm \dfrac{\pi }{2}$ $\dfrac{\pi }{2}$ 0 ${ {\rm{arctan} } }\left(\dfrac{ {a{y^{E'} } } }{ {b{x^{E'} } } }\right)$ ${x^{E'}}$ $\dfrac{{a\alpha }}{{\sqrt {{\alpha ^2} + {\beta ^2}} }}$ 0 0 $a$ $\dfrac{\alpha }{{{e^2}}}$ ${y^{E'}}$ $\dfrac{{a\beta }}{{\sqrt {{\alpha ^2} + {\beta ^2}} }}$ $ \pm b$ $b$ 0 $ \pm a\sqrt {\left( {1 - {e^2}} \right)\left( {1 - \dfrac{{{\alpha ^2}}}{{{e^4}{a^2}}}} \right)} $ ${d^{E'}}$ $\left| {\sqrt {{\alpha ^2} + {\beta ^2}} - a} \right|$ $b$ $\left| {b - \beta } \right|$ $\left| {\alpha - a} \right|$ $\sqrt {\left( {1 - {e^2}} \right)\left( {{a^2} - \dfrac{{{\alpha ^2}}}{{{e^2}}}} \right)} $ 表 2 平面内一点与双曲线(左支)之间最近距离的封闭解情况
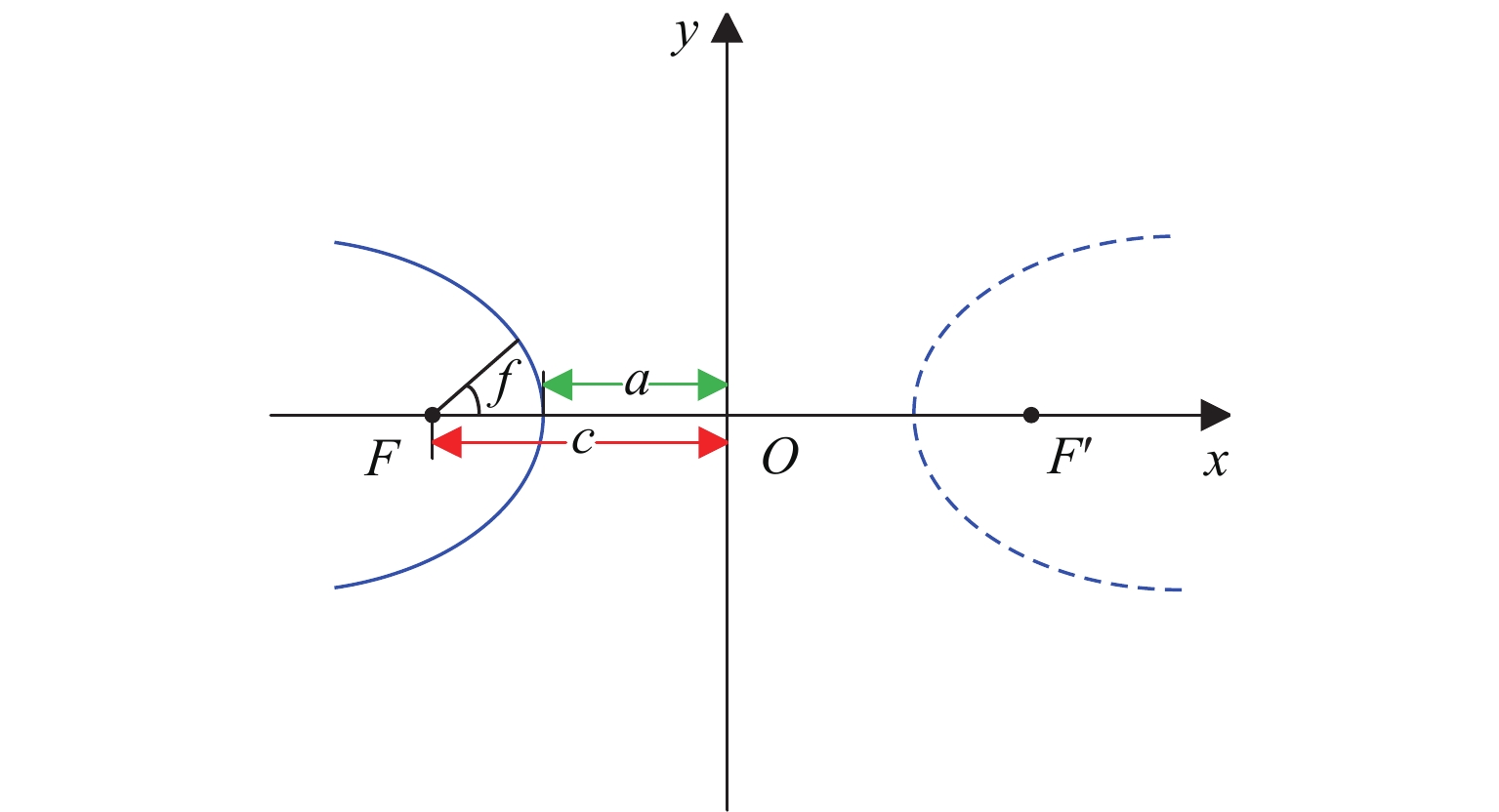
Table 2. Cases of minimum distance between a hyperbola (left branch) and a coplanar point with closed-form solution
$\alpha = 0,\;\;\beta \ne 0$ $\beta = 0$ $\alpha = 0$ $\alpha > 0$ $\alpha < 0$ $\dfrac{\alpha }{{{e^2}}} > - a$ $\dfrac{\alpha }{{{e^2}}} \leqslant - a$ ${u^{H'}}$ ${{\rm{arsinh}}} \dfrac{ { {y^{H'} } } }{b}$ 0 0 0 ${ {\rm{arsinh} } } \left(\dfrac{ { {y^{H'} } } }{b} \right)$ ${x^{H'}}$ $ - \sqrt {{a^2} + {\beta ^2}\dfrac{{{e^2} - 1}}{{{e^4}}}} $ $ - a$ $ - a$ $ - a$ $\dfrac{\alpha }{{{e^2}}}$ ${y^{H'}}$ $\beta \dfrac{{{e^2} - 1}}{{{e^2}}}$ 0 0 0 $ \pm \sqrt {\dfrac{{{e^2} - 1}}{{{e^4}}}{\alpha ^2} - {a^2}\left( {{e^2} - 1} \right)} $ ${d^{H'}}$ $\sqrt {{a^2} + \dfrac{{{\beta ^2}}}{{{e^4}}}} $ $a$ $\alpha + a$ $\left| {\alpha + a} \right|$ $\sqrt {\left( {{e^2} - 1} \right)\left( {\dfrac{{{\alpha ^2}}}{{{e^2}}} - {a^2}} \right)} $ 表 3 椭圆轨道间MOID计算结果
Table 3. Calculation results of MOID between ellipses
试验组 第1组 第2组 第3组 第4组 椭圆1 [1.3, 0.8, 20, 40, 30] [1.3, 0, 5, 25, 70] [0.8, 0.6, 50, 90, 15] [5, 0, 1, 23, 160, 38] 椭圆2 [1.6, 0.2, 10, 10, 40] [2, 0.2, 25, 60, 10] [2, 0, 5, 5, 45] [40, 0.5, 10, 5, 12] MOID参考值/km 13607164.6687 44898348.7506 109321147.5369 2202694177.5332 MOID /km 1.36071661×107 4.48983535×107 1.09321159×108 2.20269441×109 误差/km 1.43393412 4.73142715 11.52041380 232.122031 误差率/(%) 1.05380816×10–5 1.05380872×10–5 1.05381384×10–5 1.05380962×10–5 表 4 椭圆轨道与双曲线轨道间MOID计算结果
Table 4. Calculation results of MOID between ellipse and hyperbola
轨道试验组 第1组 第2组 椭圆 [5, 0.1, 123, 160, 38] [3, 0.6, 18, 110, 60] 双曲线 [2, 1.1, 10, 10, 50] [8, 1.9, 40, 25, 30] 双曲线为次要轨道MOID/km 3.963177176748018×108 6.298038462422734×108 双曲线为基准轨道MOID/km 3.963177176747759×108 6.298038462422662×108 误差/km 2.59280205×10–5 7.27176666×10–6 表 5 仿真算例轨道详细参数
Table 5. Detailed parameters of simulation example
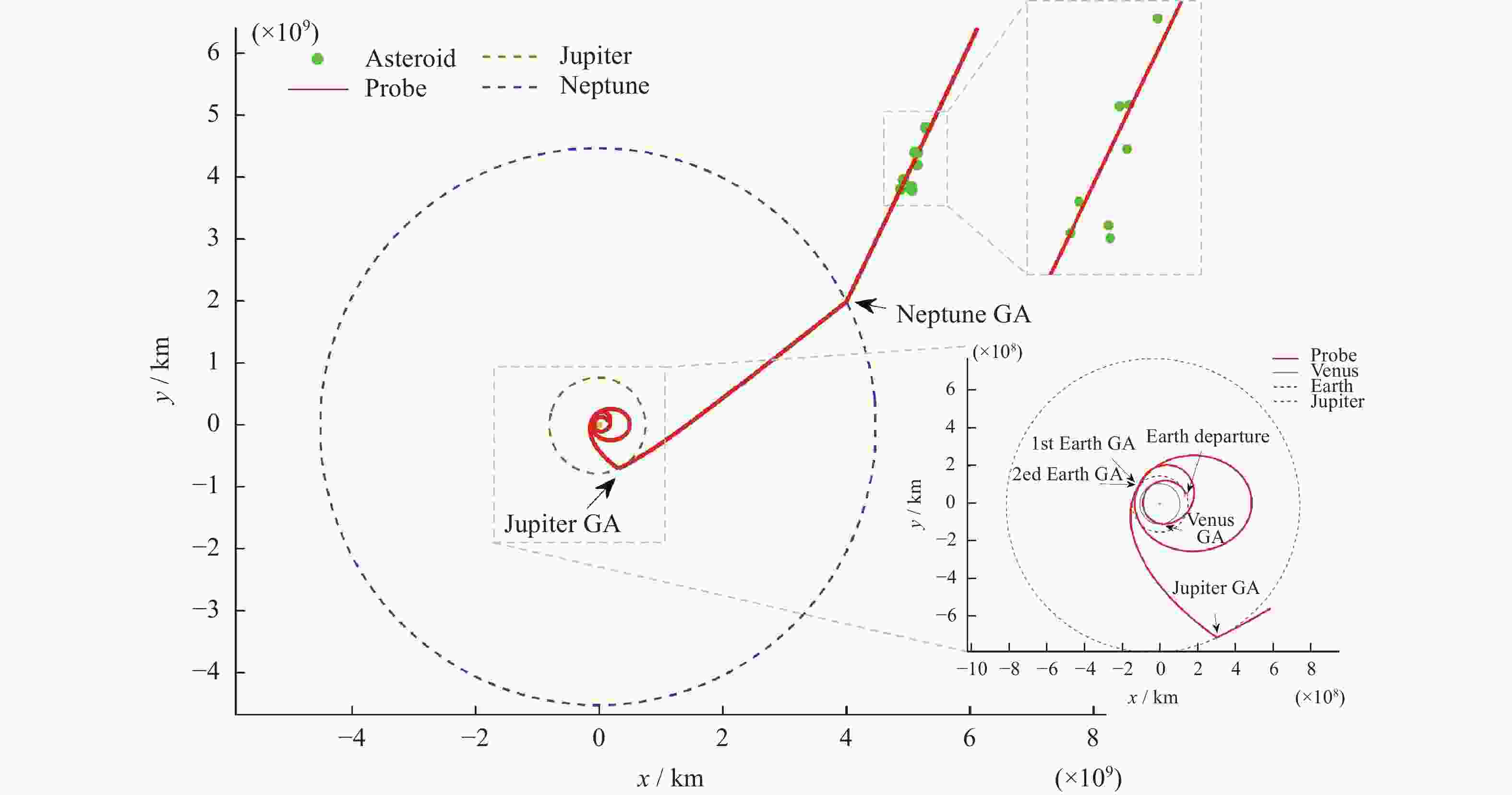
事件 数值 地球出发时间(UTC) 13 Oct. 2026 地球出发C3/(km2·s–2) 16.4445 VGA时间(UTC) 25 Mar. 2027 VGA相对速度/(km·s–1) 8.5820 1st EGA时间(UTC) 9 Feb. 2028 1st EGA相对速度/(km·s–1) 11.2555 2nd EGA时间(UTC) 4 Feb. 2031 2nd EGA相对速度/(km·s–1) 12.0082 JGA时间(UTC) 7 Jun. 2032 JGA相对速度/(km·s–1) 14.1421 NGA时间(UTC) 10 Jul. 2037 NGA相对速度/(km·s–1) 26.9402 1 Oct. 2049日心距离/AU 101.0975 1 Oct. 2049方向
黄经,黄纬/(°)51.4184,
–1.8973表 6 小行星顺访探测目标筛选计算时间
Table 6. Calculation time of asteroid follow-up exploration targets screening
可接近标准/km 基于MOID计算的目标筛选方法 传统筛选方法 预筛选耗时/s 预筛选出目标个数 总耗时/s 总耗时/s 108 263.629173 482 2443.97877 11328.379607 1.5×108 286.552569 684 3623.881037 11345.618512 2×108 269.319030 861 4028.859127 12544.087489 2.5×108 308.697467 1005 5181.535382 12985.271235 3×108 316.483332 1136 6319.317418 12993.934105 表 7 接近距离小于2×108 km的小行星
Table 7. Approaching asteroids less than 2×108 km away
小行星名称 MOID/km 接近时间(UTC) 最近距离/km 半长轴/AU 偏心率 轨道倾角/(o) 2015 RT277 75019596.201994 24 Mar. 2040 82959415.779609 39.579 0.178 5.5 2015 RC278 54281258.745103 15 Sept. 2039 94084697.708552 43.665 0.081 4.6 2013 WG114 107052981.887229 8 Nov. 2039 121224575.680900 44.306 0.068 1.5 2013 UR22 50935517.061476 9 Nov. 2040 196735855.187885 43.958 0.085 1.4 2006 QB181 97924800.048774 17 May 2030 186030288.037780 43.687 0.04 2.2 2003 QV90 65773073.620961 12 Nov. 2039 130834664.641326 43.814 0.052 2.4 2001 QQ297 132369997.497804 2 Jun. 2040 170037438.432199 44.343 0.085 4.4 2001 QO297 77750095.885436 22 Oct. 2039 122746214.301738 43.052 0.034 1.1 -
[1] HUANG J C, JI J H, YE P J, et al. The ginger-shaped asteroid 4179 Toutatis: new observations from a successful flyby of Chang’E-2[J]. Scientific Reports, 2013, 3: 3411 doi: 10.1038/srep03411 [2] DAMARIO L A, BYRNES D V. Interplanetary trajectory design for the Galileo mission[C]//Proceedings of the 21 st Aerospace Sciences Meeting. Reno: AIAA, 1983: 1-9. DOI: 10.2514/6.1983-99 [3] 乔栋, 黄江川, 崔平远, 等. 嫦娥二号卫星飞越探测小行星的目标选择[J]. 中国科学: 技术科学, 2013, 43(6): 602-608 doi: 10.1360/092013-313QIAO Dong, HUANG Jiangchuan, CUI Pingyuan, et al. Target selection of Chang’E-2 for asteroid exploration[J]. Scientia Sinica Technologica, 2013, 43(6): 602-608 doi: 10.1360/092013-313 [4] 陈杨, 宝音贺西, 李俊峰. 木星探测轨道分析与设计[J]. 天文学报, 2012, 53(2): 106-118 doi: 10.3969/j.issn.0001-5245.2012.02.002CHEN Yang, BAOYIN Hexi, LI Junfeng. Jupiter exploration mission analysis and trajectory design[J]. Acta Astronomica Sinica, 2012, 53(2): 106-118 doi: 10.3969/j.issn.0001-5245.2012.02.002 [5] 刘磊, 刘勇, 曹建峰, 等. “嫦娥二号”探测小行星任务转移轨道设计[J]. 宇航学报, 2014, 35(3): 262-268 doi: 10.3873/j.issn.1000-1328.2014.03.003LIU Lei, LIU Yong, CAO Jianfeng, et al. Mission design of the Chang’E-2 asteroid exploration[J]. Journal of Astronautics, 2014, 35(3): 262-268 doi: 10.3873/j.issn.1000-1328.2014.03.003 [6] HEDO J M, RUÍZ M, PELÁEZ J. On the minimum orbital intersection distance computation: a new effective method[J]. Monthly Notices of the Royal Astronomical Society, 2018, 479(3): 3288-3299 doi: 10.1093/mnras/sty1598 [7] 张佳文. 太阳系边际探测任务轨道优化设计[D]. 北京: 中国科学院大学(中国科学院国家空间科学中心), 2020: 63-85ZHANG Jiawen. Trajectory Design and Optimization for the Solar System Boundary Exploration Mission[D]. Beijing: National Space Science Center, the Chinese Academy of Sciences, 2020: 63-85 [8] WLODARCZYK I. The potentially dangerous asteroid (99942) Apophis[J]. Monthly Notices of the Royal Astronomical Society, 2013, 434(4): 3055-3060 doi: 10.1093/mnras/stt1227 [9] CASANOVA D, TARDIOLI C, LEMAÎTRE A. Space debris collision avoidance using a three-filter sequence[J]. Monthly Notices of the Royal Astronomical Society, 2014, 442(4): 3235-3242 doi: 10.1093/mnras/stu1065 [10] DYBCZYŃSKI P A, JOPEK T J, SERAFIN R A. On the minimum distance between two Keplerian orbits with a common focus[J]. Celestial Mechanics, 1986, 38(4): 345-356 doi: 10.1007/BF01238925 [11] KHOLSHEVNIKOV K V, VASSILIEV N N. On the distance function between two Keplerian elliptic orbits[J]. Celestial Mechanics and Dynamical Astronomy, 1999, 75(2): 75-83 doi: 10.1023/A:1008312521428 [12] GRONCHI G F. An algebraic method to compute the critical points of the distance function between two Keplerian orbits[J]. Celestial Mechanics and Dynamical Astronomy, 2005, 93(1): 295-325 doi: 10.1007/s10569-005-1623-5 [13] MILISAVLJEVIĆ S. The proximities of asteroids and critical points of the distance function[J]. Serbian Astronomical Journal, 2010, 180: 91-102 doi: 10.2298/SAJ1080091M [14] WISNIOWSKI T, RICKMAN H. Fast geometric method for calculating accurate minimum orbit intersection distances (MOIDs)[J]. Acta Astronomica, 2013, 63(2): 293-307 [15] DEREVYANKA A E. A method for the fast MOID computation for two confocal heliocentric orbits[J]. J. Samara State Tech. Univ. Ser. Phys Math. Sci., 2014, 4(37): 144-156 doi: 10.14498/vsgtu1344 [16] HEDO J M, FANTINO E, RUÍZ M, et al. Minimum orbital intersection distance: an asymptotic approach[J]. Astronomy & Astrophysics, 2020, 633: A22 doi: 10.1051/0004-6361/201936502 [17] BALUEV R V. Fast error-safe MOID computation involving hyperbolic orbits[J]. Astronomy and Computing, 2021, 34: 100440 doi: 10.1016/j.ascom.2020.100440 [18] WEISSTEIN E W. Halley’s Method[EB/OL]. MathWorld – A Wolfram Web Resource. (2021-03-18)[2021-03-25]. http://mathworld.wolfram.com/HalleysMethod.html. [19] RICKMAN H, WISNIOWSKI T. Application for Computation of MOIDs[EB/OL]. Space Research Center Polish Academy of Science. [2020-03-10]. http://moid.cbk.waw.pl/orbity/default/index [20] 吴伟仁, 于登云, 黄江川, 等. 太阳系边际探测研究[J]. 中国科学: 信息科学, 2019, 49(1): 1-16 doi: 10.1360/N112018-00273WU Weiren, YU Dengyun, HUANG Jiangchuan, et al. Exploring the solar system boundary[J]. Scientia Sinica Informationis, 2019, 49(1): 1-16 doi: 10.1360/N112018-00273 [21] The International Astronomical Union. Lists and Plots: Minor Planets[EB/OL]. IAU Minor Planet Center. [2020-03-12]. https://minorplanetcenter.net/iau/lists/MPLists.html. [22] 刘林, 胡松杰, 王歆. 航天动力学引论[M]. 南京: 南京大学出版社, 2006: 21-52LIU Lin, HU Songjie, WANG Xin. An Introduction of Astrodynamics[M]. Nanjing: Nanjing University Press, 2006: 21-52 [23] 季江徽, 刘林. 近地小行星与地球的交会问题[J]. 中国科学(A辑), 2000, 30(4): 379-384 doi: 10.3969/j.issn.1674-7216.2000.04.013JI Jianghui, LIU Lin. The intersection of near earth asteroids and the earth[J]. Science in China (Series A) , 2000, 30(4): 379-384 doi: 10.3969/j.issn.1674-7216.2000.04.013 [24] 李小玉. 深空借力飞行/小推力轨道设计与优化[D]. 北京: 中国科学院研究生院(空间科学与应用研究中心), 2010: 23-27LI Xiaoyu. Trajectory Design and Optimization of Gravity-assist/Low-thrust For Deep Space Exploration[D]. Beijing: National Space Science Center, CAS, 2010: 23-27 [25] 李俊峰, 宝音贺西, 蒋方华. 深空探测动力学与控制[M]. 北京: 清华大学出版社, 2014: 110-127LI Junfeng, BAOYIN Hexi, JIANG Fanghua. Dynamics and Control of Interplanetary Flight[M]. Beijing: Tsinghua University Press, 2014: 110-127 -
-





 下载:
下载: