基于贝叶斯证据的全球地磁场模型主磁场阶数分析
doi: 10.11728/cjss2023.04.2022-0009 cstr: 32142.14.cjss2023.04.2022-0009
Analysis of Global Geomagnetic Main Field Model Order Based on Bayesian Evidence
-
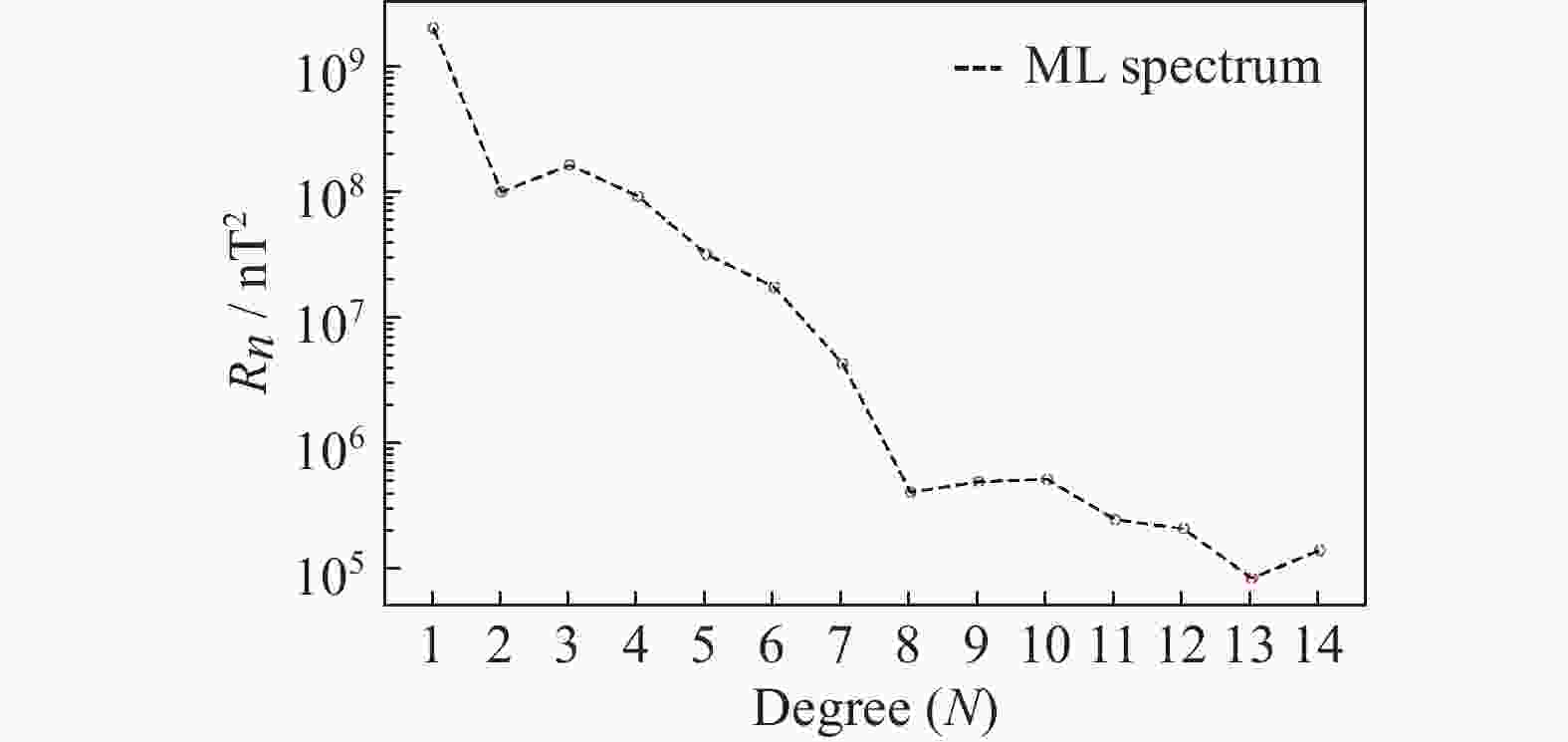
摘要: 全球主磁场模型描述了主磁场的时空分布特征。模型的主磁场阶数是构建主磁场模型的关键问题之一。使用贝叶斯推理分析全球主磁场模型，依据贝叶斯证据比较模型阶数，为主磁场的阶数分析提供一种统计依据。利用Swarm卫星磁测数据，估计不同阶数的主磁场模型的证据。结果表明，在1~20的模型阶数中，阶数N = 12具有全局最佳证据。参照Jefrrey’s scale的阈值区间，数据对阶数N = 12的偏好显著优于其他阶数。实验表明，主磁场阶数的证据推理可用于研究主磁场贡献，结果与14阶球谐函数的功率谱分析相匹配。Abstract: The global main magnetic field model describes the space-time distribution characteristics of the main magnetic field. The order of the main magnetic field in the model is one of the key issues to build the main magnetic field model. This paper used Bayesian inference to analyze the global geomagnetic main field model and compares model orders based on Bayesian evidence. It provided a statistical perspective for the main field order selection. Using magnetic observations from Swarm satellites, the evidence for different orders of the main field model was estimated. The results show that order N = 12 has the global best evidence in model from 1 to 20. Referring to the threshold interval given by Jefrrey’s scale, the data preference for order N = 12 is significantly better than other orders. The experiment shows that the evidence reasoning of the main magnetic field order can be used to study the main magnetic field contribution, and the results match the power spectrum analysis of spherical harmonic of order N = 14.
-
Key words:
- Geomagnetic field /
- Main field model /
- Bayesian evidence /
- Model comparison /
- Geomagnetic power spectrum
-
图 2 数据直方分布与密度曲线。（a）地磁标量强度$ {F} $，（b）观测噪声方差，（c）地壳场贡献模拟修正量，（d）外源场贡献模拟修正量
Figure 2. Data histogram distribution and density curve. (a) Geomagnetic scalar intensity $ {F} $, (b) observed noise variance, (c) simulation correction of crustal field, (d) simulation correction of external field
图 3 地壳场与外源场的主磁场修正值的KDE等高图
Figure 3. KDE contour map of the main field correction value of the crustal field and the external field
图 5 阶数$ N=3 $ 的球谐系数的后验分布
Figure 5. Posterior distribution of spherical harmonic coefficients of order N=3
图 6 利用14阶球谐函数计算的功率谱
Figure 6. Power spectrum calculated using spherical harmonics of order 14
表 1 基于SHA方法的全球地磁场模型及其主磁场对应阶数
Table 1. Geomagnetic field model and its corresponding main field order based on SHA method
下载: 导出CSV
表 2 证据因子差异度量表
Table 2. Evidence factor difference scale
$ {Z}_{i}/{Z}_{j} $ $ \mathrm{lb}{(Z}_{i}/{Z}_{j}) $ $ \mathrm{ln}({Z}_{i}/{Z}_{j}) $ $ \mathrm{lg}({Z}_{i}/{Z}_{j}) $ Evidence
against $ {H}_{i} $$1\sim3.2$ $0\sim1.7$ $0\sim1.2$ $0\sim0.5$ Weak $3.2\sim10$ $ 1.7 \sim 3.3 $ $ 1.2 \sim 2.3 $ $ 0.5 \sim 1 $ Substantial $ 10 \sim 100 $ $3.3\sim6.6$ $2.3\sim4.6$ $1\sim2$ Srtong $ > 100 $ $ > 6.6 $ $ > 4.6 $ $ > 2 $ Decisive $ > 1000 $ $ > 10 $ $ > 7 $ $ > 3 $ Beyond reasonable doubt
下载: 导出CSV
表 3 1~20阶主磁场模型的证据
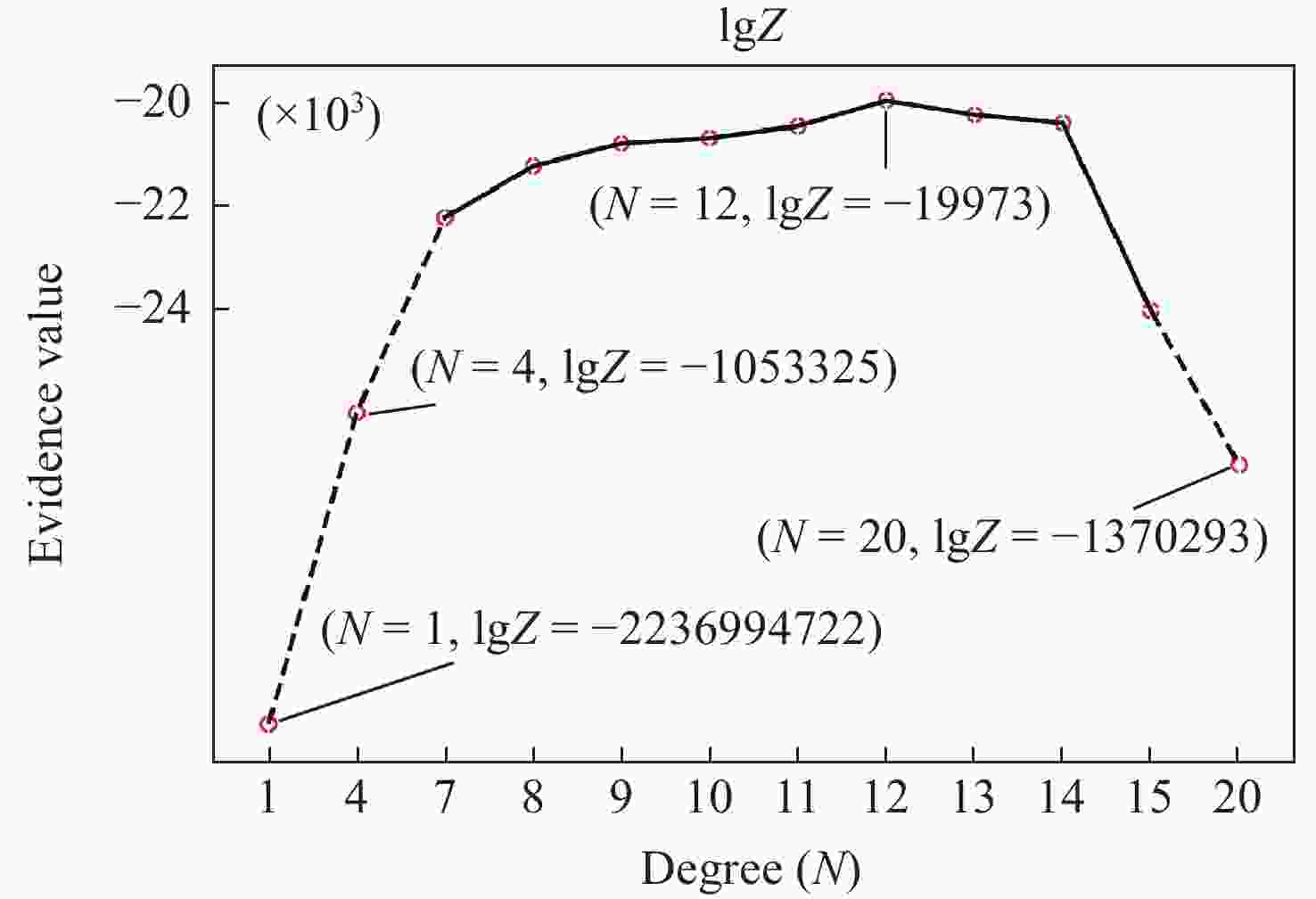
Table 3. Evidence of main field model of order 1~20
$ N $ $ \mathrm{lg}{Z}_{i} $ $ N $ $ \mathrm{lg}{Z}_{i} $ $ 1 $ $ -2236994722 $ $ 11 $ $ -20514 $ $ 2 $ $ -37342005 $ $ 12 $ $ -19973 $ $ 3 $ $ -37552523 $ $ 13 $ $ -20250 $ $ 4 $ $ -1053325 $ $ 14 $ $ -20411 $ $ 5 $ $ -96379 $ $ 15 $ $ -24028 $ $ 6 $ $ -35091 $ $ 16 $ $ -25807 $ $ 7 $ $ -22232 $ $ 17 $ $ -26269 $ $ 8 $ $ -20626 $ $ 18 $ $ -29179 $ $ 9 $ $ -20102 $ $ 19 $ $ -724596 $ $ 10 $ $ -20023 $ $ 20 $ $ -1372094 $
下载: 导出CSV
表 4 证据因子度量结果
Table 4. Result of the evidence factor measurement
Order i $ \mathrm{lg}{(Z}_{12}/{Z}_{i}) $ Evidence against $ {H}_{i} $ 10 725.2 Beyond reasonable doubt 11 496.7 Beyond reasonable doubt 13 277.2 Beyond reasonable doubt 14 438.0 Beyond reasonable doubt
下载: 导出CSV
-
[1] 徐文耀. 地球电磁现象物理学[M]. 合肥: 中国科学技术大学出版社, 2009: 87-157XU Wenyao. Physics of Electromagnetic Phenomena of the Earth[M]. Hefei: University of Science and Technology of China Press, 2009: 87-157 [2] ALKEN P, THÉBAULT E, BEGGAN C D, et al. International geomagnetic reference field: the thirteenth generation[J]. Earth, Planets and Space, 2021, 73(1): 1-25 doi: 10.1186/s40623-020-01288-x [3] YANG Y, HULOT G, VIGNERON P, et al. The CSES global geomagnetic field model (CGGM): an IGRF-type global geomagnetic field model based on data from the China seismo-electromagnetic satellite[J]. Earth, Planets and Space, 2021, 73(1): 1-21 doi: 10.1186/s40623-020-01323-x [4] HUDER L, GILLET N, FINLAY C C, et al. COV-OBS. x2: 180 years of geomagnetic field evolution from ground-based and satellite observations[J]. Earth, Planets and Space, 2020, 72(1): 1-18 doi: 10.1186/s40623-019-1127-2 [5] FINLAY C C, KLOSS C, OLSEN N, et al. The CHAOS-7 geomagnetic field model and observed changes in the south Atlantic anomaly[J]. Earth, Planets and Space, 2020, 72(1): 1-31 doi: 10.1186/S40623-020-01252-9 [6] SABAKA T J, OLSEN N, TYLER R H, et al. CM5, a pre-Swarm comprehensive geomagnetic field model derived from over 12 yr of CHAMP, Ørsted, SAC-C and observatory data[J]. Geophysical Journal International, 2015, 200(3): 1596-1626 doi: 10.1093/gji/ggu493 [7] LI S Y, LI Y L, ZHANG T J, et al. Model-independent determination of cosmic curvature based on the Padé approximation[J]. The Astrophysical Journal, 2019, 887(1): 36 doi: 10.3847/1538-4357/ab5225 [8] BURNHAM K P, ANDERSON D R. Multimodel inference: understanding AIC and BIC in model selection[J]. Sociological Methods & Research, 2004, 33(2): 261-304 [9] BELTRÁN M, GARCIA-BELLIDO J, LESGOURGUES J, et al. Bayesian model selection and isocurvature perturbations[J]. Physical Review D, 2005, 71(6): 063532 doi: 10.1103/PhysRevD.71.063532 [10] TROTTA R. Applications of Bayesian model selection to cosmological parameters[J]. Monthly Notices of the Royal Astronomical Society, 2007, 378(1): 72-82 doi: 10.1111/j.1365-2966.2007.11738.x [11] ARREGUI I, RAMOS A A, DÍAZ A J. Bayesian analysis of multiple harmonic oscillations in the solar corona[J]. The Astrophysical Journal Letters, 2013, 765(1): L23 doi: 10.1088/2041-8205/765/1/L23 [12] BRIDGES M, LASENBY A N, HOBSON M P. A Bayesian analysis of the primordial power spectrum[J]. Monthly Notices of the Royal Astronomical Society, 2006, 369(3): 1123-1130 doi: 10.1111/j.1365-2966.2006.10351.x [13] BALBI A, BRUNI M, QUERCELLINI C. ΛαDM: observational constraints on unified dark matter with constant speed of sound[J]. Physical Review D, 2007, 76(10): 103519 doi: 10.1103/PhysRevD.76.103519 [14] NESSERIS S, GARCIA-BELLIDO J. Is the Jeffreys’ scale a reliable tool for Bayesian model comparison in cosmology[J]. Journal of Cosmology and Astroparticle Physics, 2013, 2013(8): 036 doi: 10.1088/1475-7516/2013/08/036 [15] 胡传鹏, 孔祥祯, WAGENMAKERS E J, 等. 贝叶斯因子及其在JASP中的实现[J]. 心理科学进展, 2018, 26(6): 951-965 doi: 10.3724/SP.J.1042.2018.00951HU Chuanpeng, KONG Xiangzhen, WAGENMAKERS E J, et al. The Bayes factor and its implementation in JASP: a practical primer[J]. Advances in Psychological Science, 2018, 26(6): 951-965 doi: 10.3724/SP.J.1042.2018.00951 [16] MACKAY D J C. A practical Bayesian framework for backpropagation networks[J]. Neural Computation, 1992, 4(3): 448-472 doi: 10.1162/neco.1992.4.3.448 [17] MACKAY D J C. Information-based objective functions for active data selection[J]. Neural Computation, 1992, 4(4): 590-604 doi: 10.1162/neco.1992.4.4.590 [18] 徐文耀, 区加明, 杜爱民. 地磁场全球建模和局域建模[J]. 地球物理学进展, 2011, 26(2): 398-415 doi: 10.3969/j.issn.1004-2903.2011.02.002XU Wenyao, OU Jiaming, DU Aimin. Geomagnetic field modelling for the globe and a limited region[J]. Progress in Geophysics, 2011, 26(2): 398-415 doi: 10.3969/j.issn.1004-2903.2011.02.002 [19] SKILLING J. Nested sampling[J]. AIP Conference Proceedings, 2004, 735(1): 395-405 [20] FEROZ F, HOBSON M P, BRIDGES M. MULTINEST: an efficient and robust Bayesian inference tool for cosmology and particle physics[J]. Monthly Notices of the Royal Astronomical Society, 2009, 398(4): 1601-1614 doi: 10.1111/j.1365-2966.2009.14548.x [21] BUCHNER J. Collaborative nested sampling: Big data versus complex physical models[J]. Publications of the Astronomical Society of the Pacific, 2019, 131(1004): 108005 doi: 10.1088/1538-3873/aae7fc [22] BUCHNER J. Nested sampling methods[OL]. arXiv preprint arXiv: 2101.09675, 2021 [23] KASS R E, RAFTERY A E. Bayes factors[J]. Journal of the American Statistical Association, 1995, 90(430): 773-795 doi: 10.1080/01621459.1995.10476572 [24] JEFFREYS H. The Theory of Probability[M]. 3 rd ed. Oxford: Oxford University Oxford, 1998 -
-
下载:
计量
- 文章访问数: 669
- HTML全文浏览量: 222
- PDF下载量: 125
-
被引次数:
0(来源:Crossref)
0(来源:其他)
