An Improved HVQ Algorithm for Compression and Rendering of Space Environment Volume Data with Multi-correlated Variables
doi: 10.11728/cjss2023.04.2022-0020 cstr: 32142.14.cjss2023.04.2022-0020
-
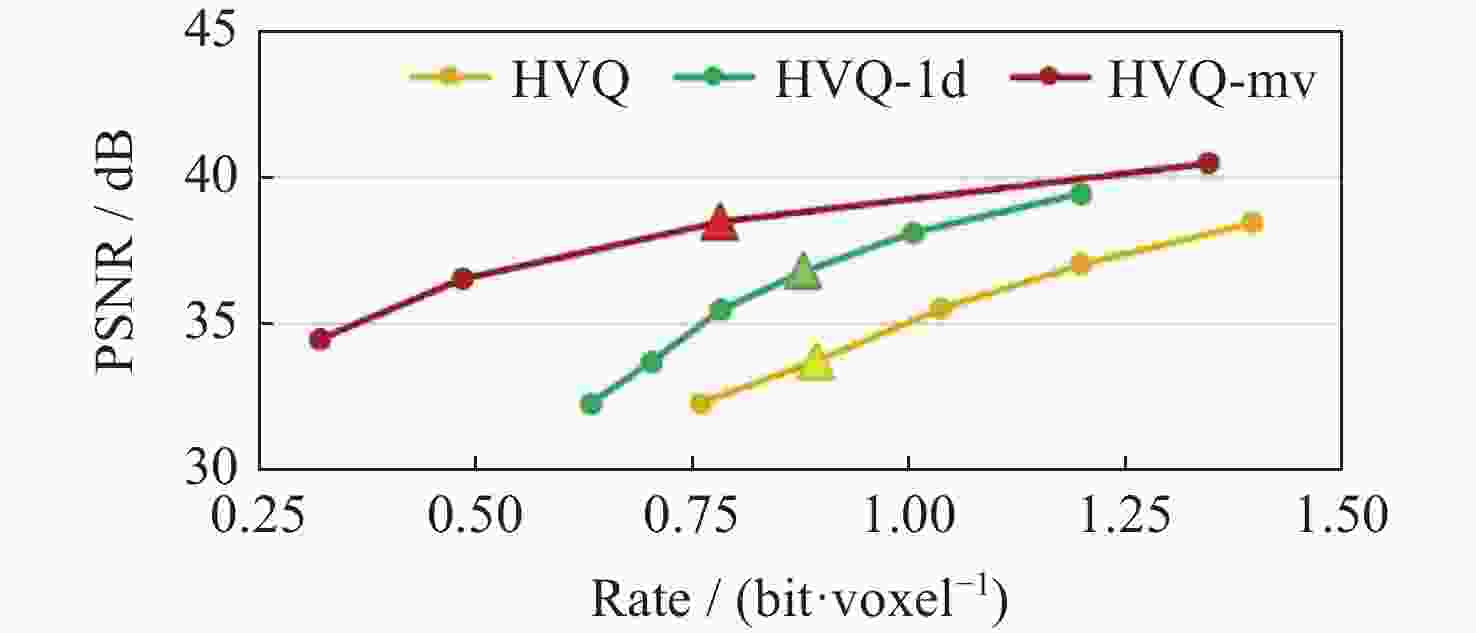
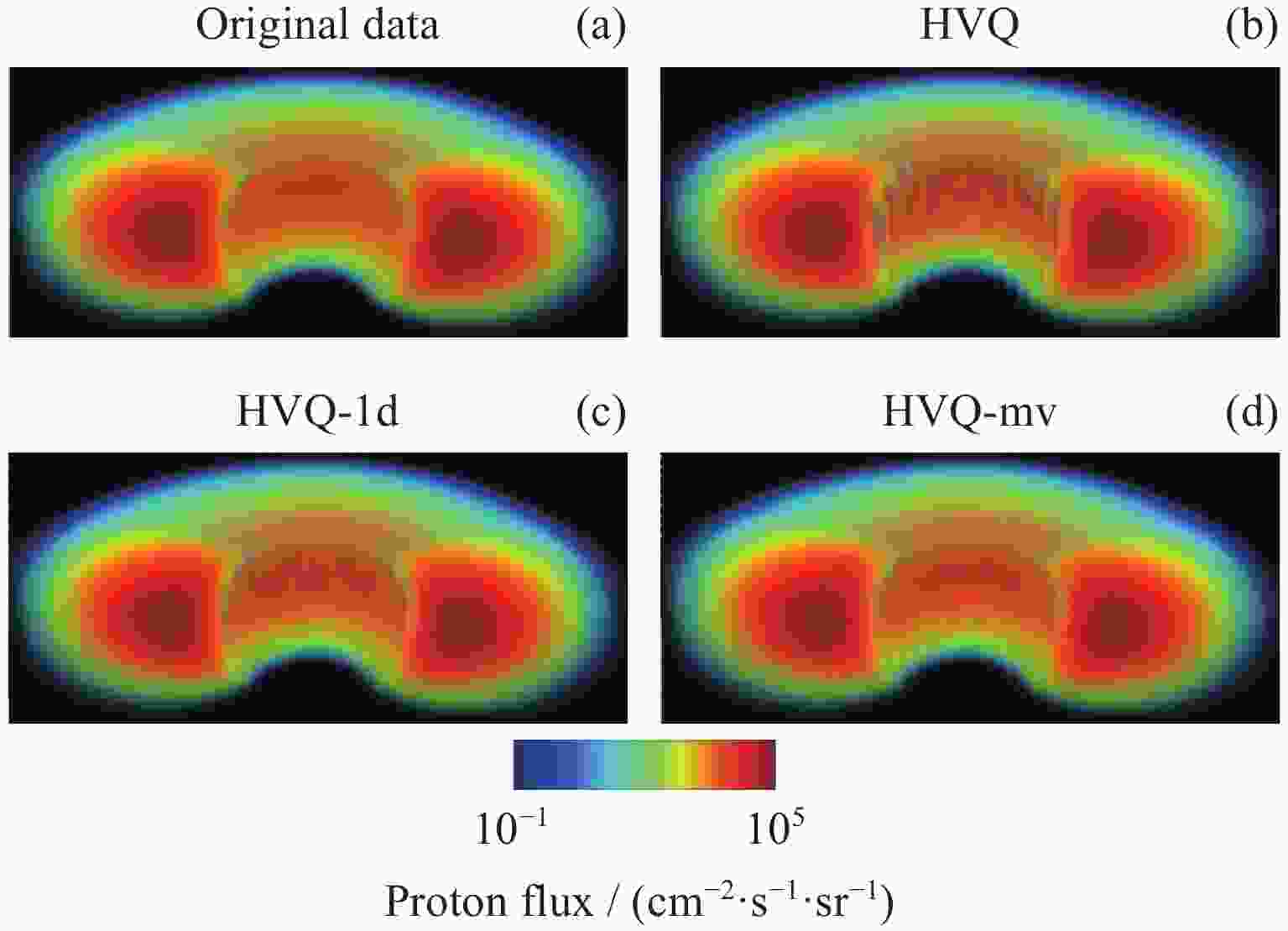
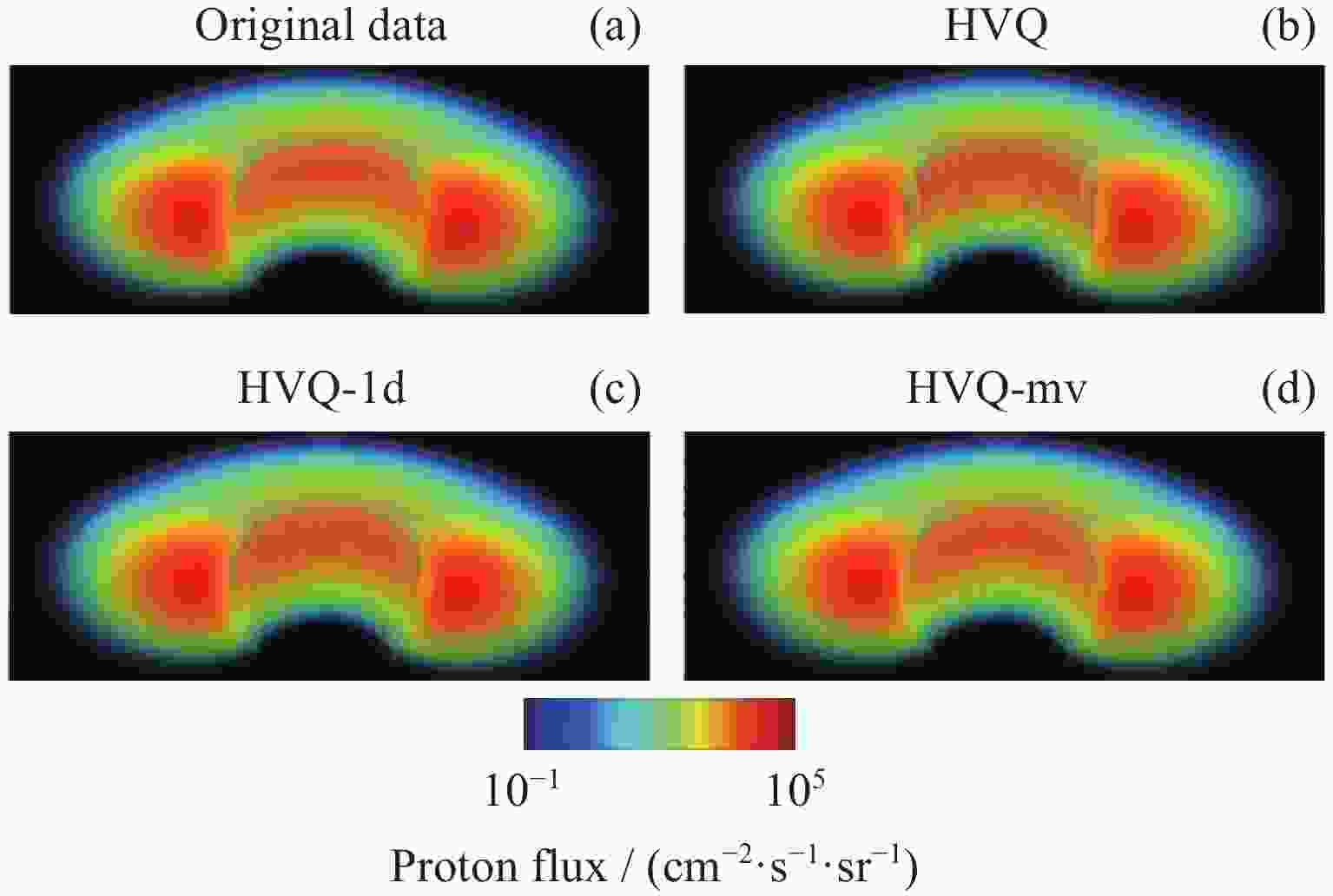
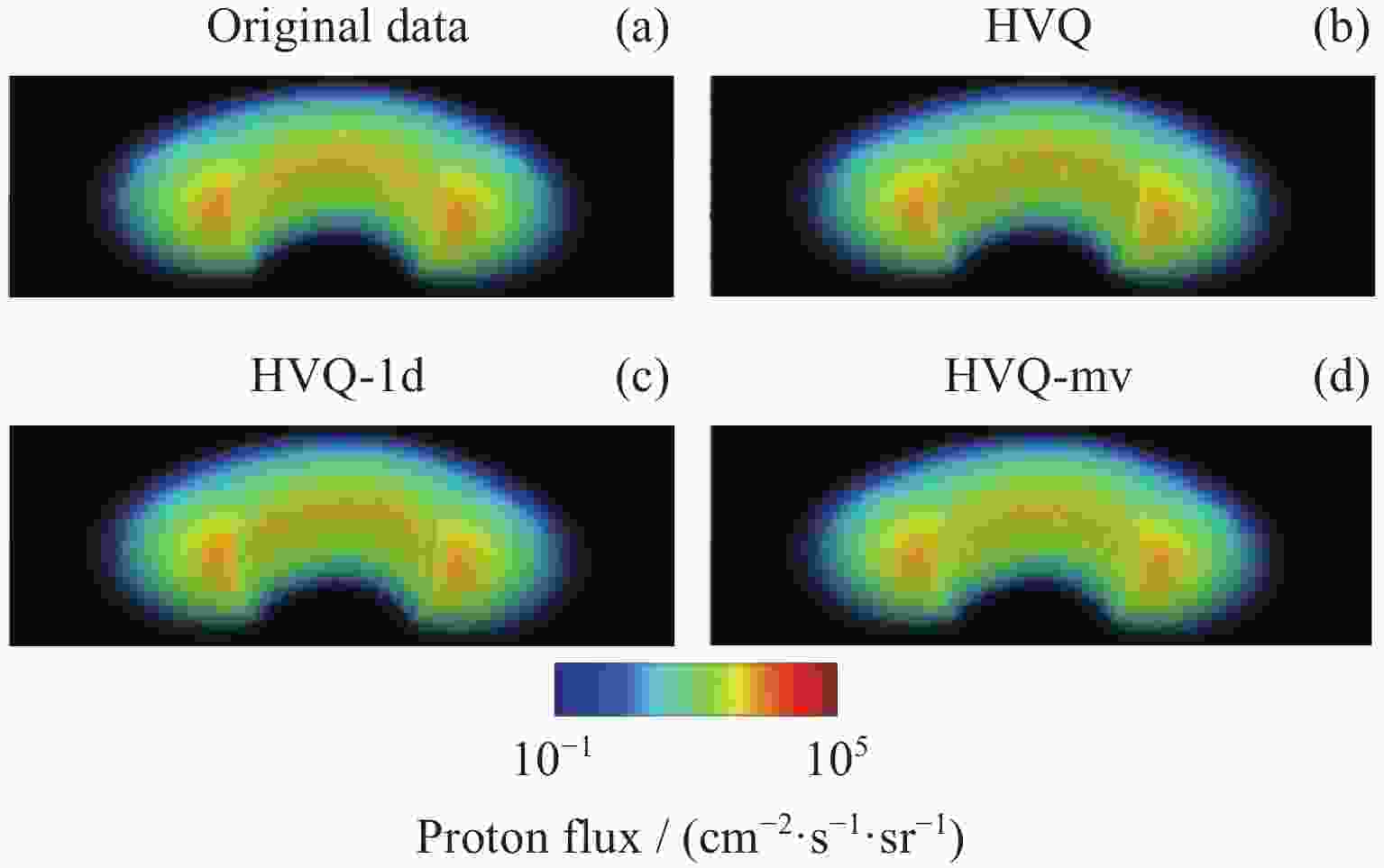
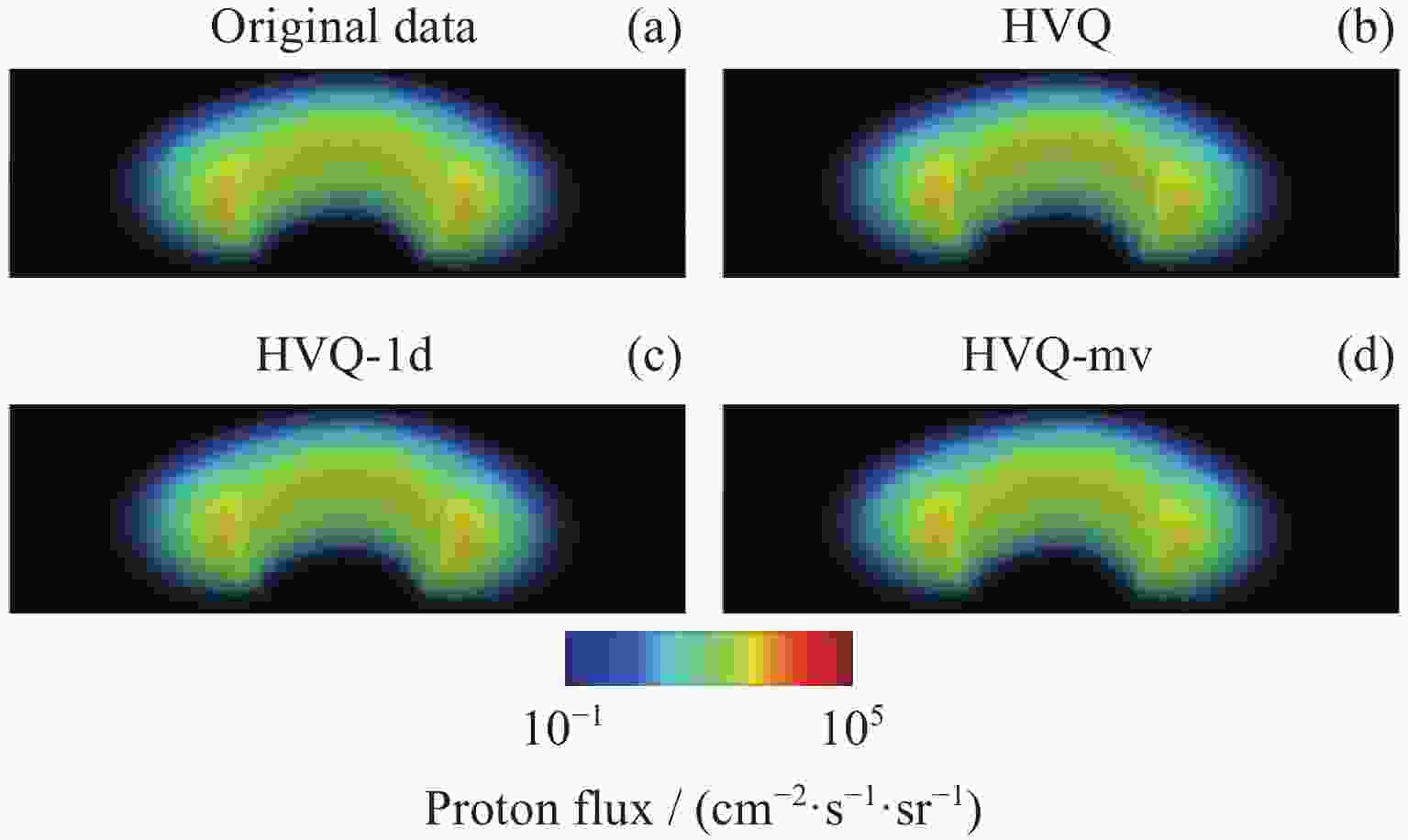
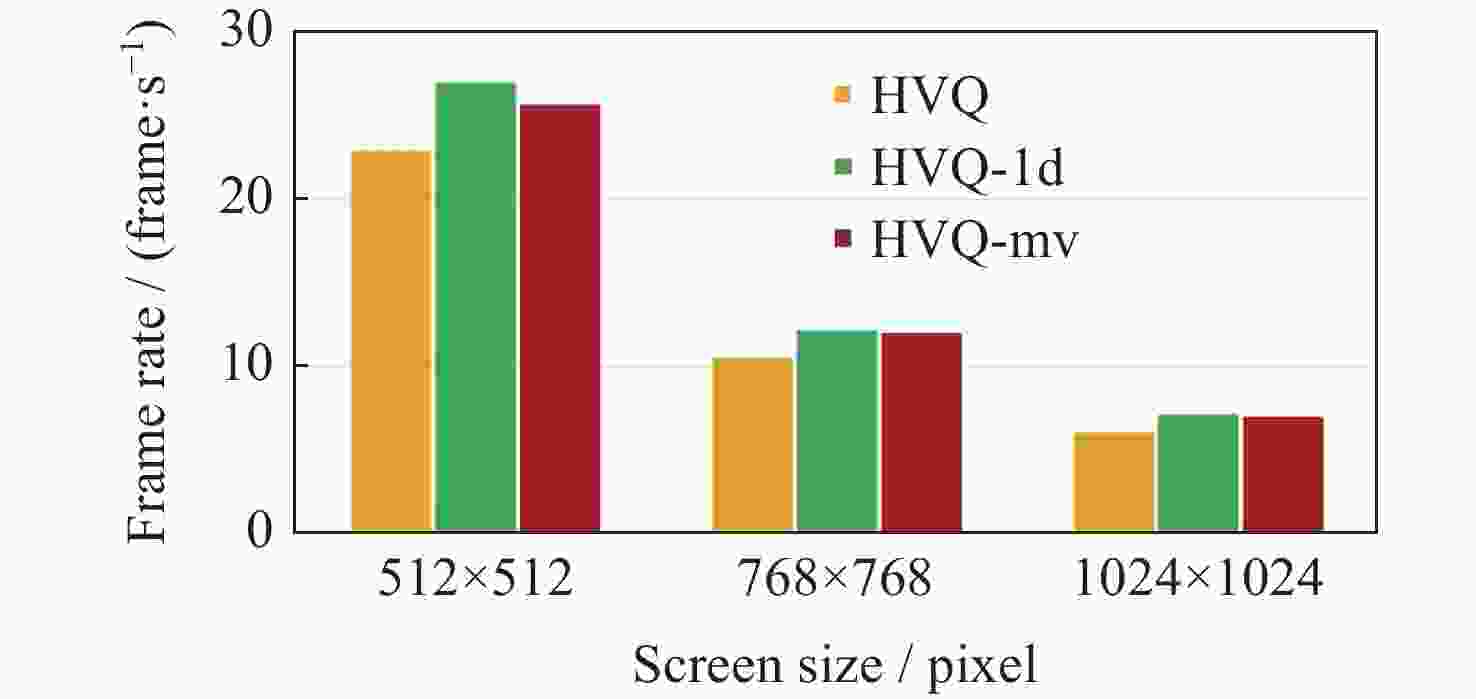
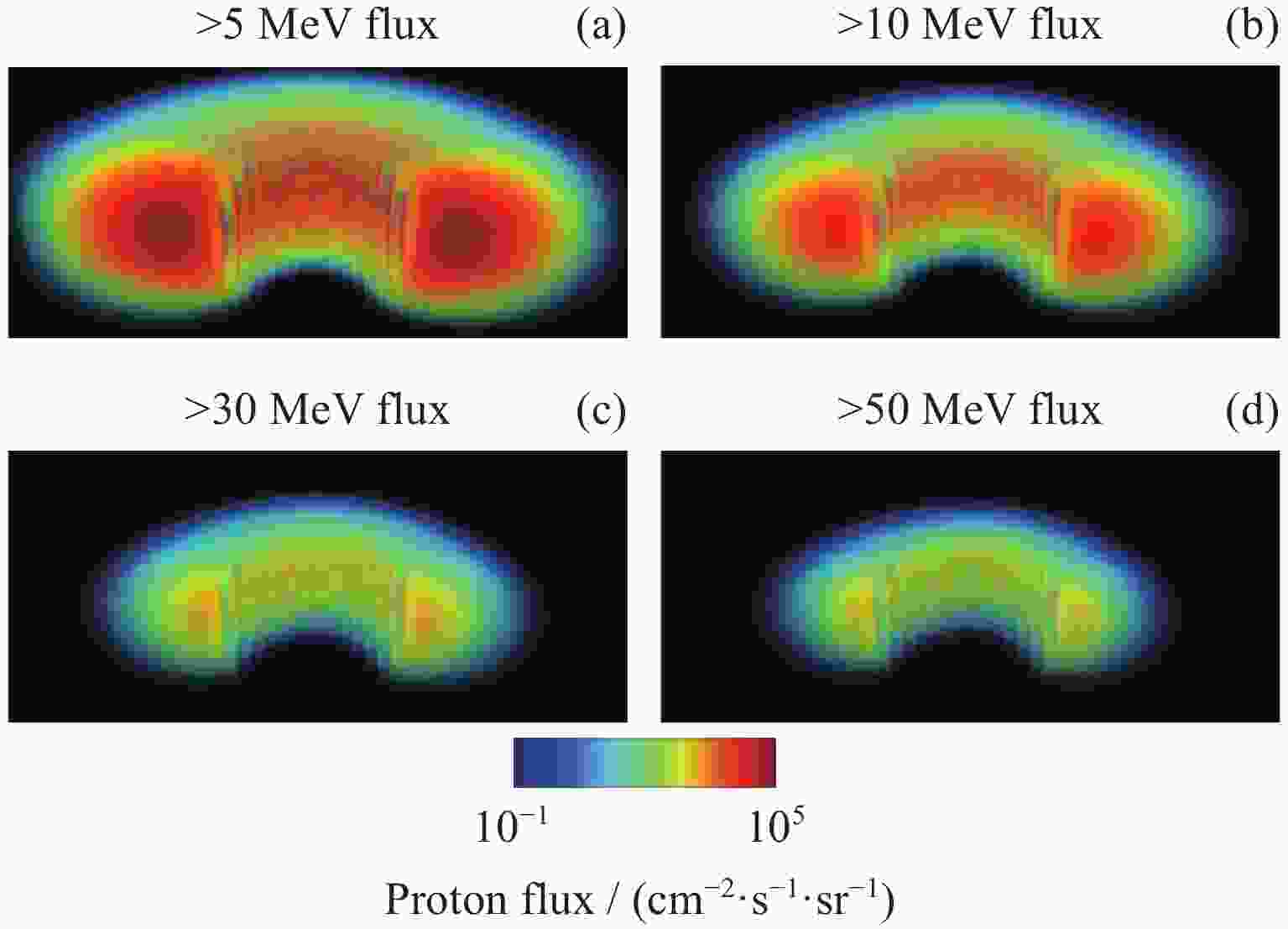
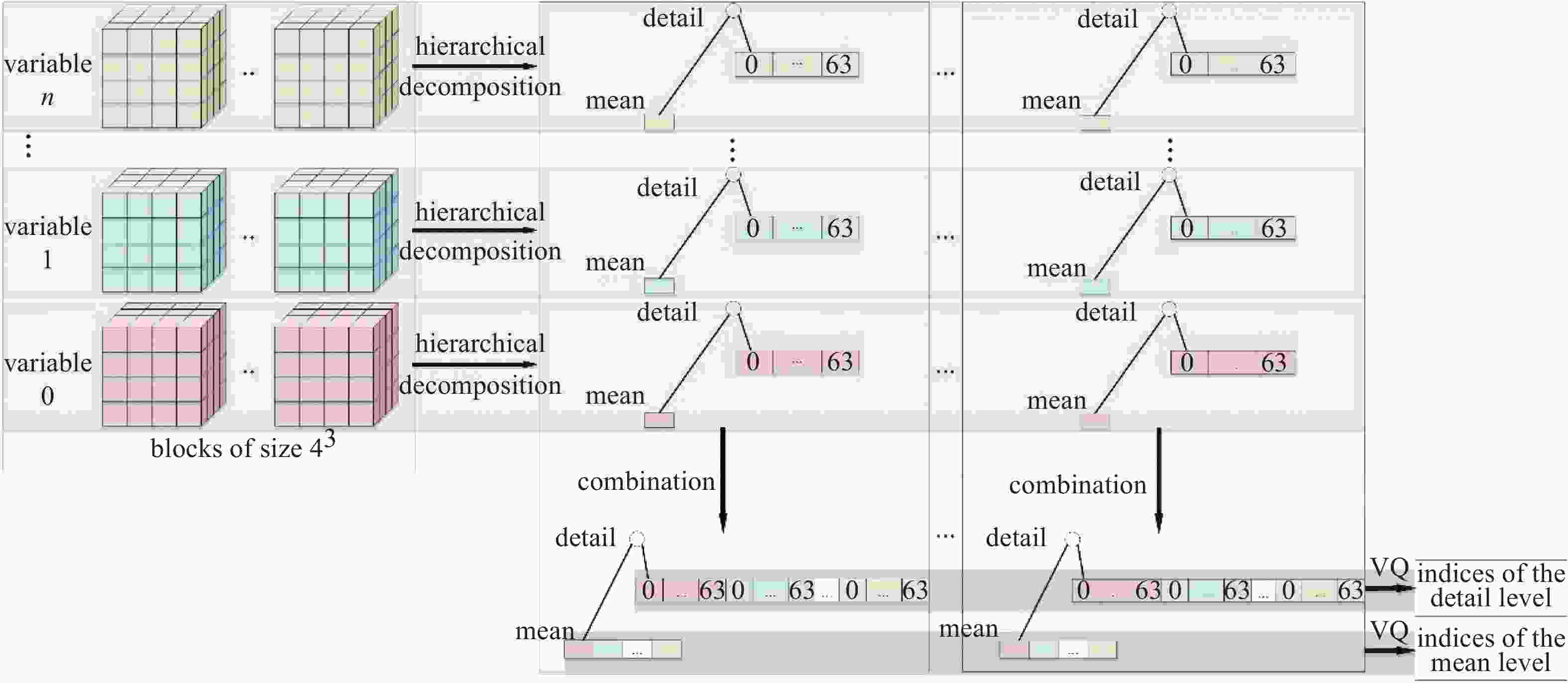
Abstract: Volume visualization can not only illustrate overall distribution but also inner structure and it is an important approach for space environment research. Space environment simulation can produce several correlated variables at the same time. However, existing compressed volume rendering methods only consider reducing the redundant information in a single volume of a specific variable, not dealing with the redundant information among these variables. For space environment volume data with multi-correlated variables, based on the HVQ-1d method we propose a further improved HVQ method by compositing variable-specific levels to reduce the redundant information among these variables. The volume data associated with each variable is divided into disjoint blocks of size 43 initially. The blocks are represented as two levels, a mean level and a detail level. The variable-specific mean levels and detail levels are combined respectively to form a larger global mean level and a larger global detail level. To both global levels, a splitting based on a principal component analysis is applied to compute initial codebooks. Then, LBG algorithm is conducted for codebook refinement and quantization. We further take advantage of progressive rendering based on GPU for real-time interactive visualization. Our method has been tested along with HVQ and HVQ-1d on high-energy proton flux volume data, including > 5, > 10, > 30 and > 50 MeV integrated proton flux. The results of our experiments prove that the method proposed in this paper pays the least cost of quality at compression, achieves a higher decompression and rendering speed compared with HVQ and provides satisficed fidelity while ensuring interactive rendering speed.
-
0. Introduction
Volume visualization can not only illustrate overall distribution but also inner structure and it is an important approach for space environment research[1–3]. By means of programmability in graphics hardware, real-time interactive large-scale volume rendering can be realized[1,4]. With the development of space environment explorations[5] and physical models, scientists can simulate many space environment situations in detail, each simulation producing several variables, hundreds of time steps and millions of voxels. Because of the limited memory capacity, it is difficult to render such large volume data on GPU directly. Vector Quantization (VQ)[6], as a Compressed Volume Rendering (CVR) method[7], can reduce the volume data set to a significantly smaller size and support decompressing at rendering time. Because of the simple, localized and uniform decoding, VQ has been widely applied in many domains[1,7,8]. Hierarchical Vector Quantization (HVQ) is one of the most common VQ methods and can achieve high reconstruction quality, however at the cost of a low compression rate[2,9–11]. Therefore, Hierarchical Vector Quantization With 1 Detail Level (HVQ-1 d) is proposed to raise the compression rate while maintaining good fidelity based on the variation characteristics of space environment[1]. However, these methods just reduce the redundant information in each volume of each variable. Most space environment simulations can generate several correlated variables, such as particle flux values of different channels, density values of different atmospheric components, etc. There must be massive similar variations or redundant information among these variables. Based on these, a further improved HVQ algorithm, Hierarchical Vector Quantization based on multi-correlated variables (HVQ-mv), is described in this paper.
This paper is organized into five sections. In the following section, related works are reviewed. In Section 2, our improved HVQ algorithm is described. In Section 3, the experiments are introduced, and the results and comparisons are presented. In the last section, a conclusion has been drawn for our paper.
1. Related Works
VQ technology has been introduced in CVR by Ning and Hesselink[6,8]. Firstly, the entire volume is divided into disjoint blocks of n×m×k. Then by vector quantization, a codebook is generated and these blocks are replaced by indices in this codebook. This method can obtain a high compression rate, however, at the cost of bad reconstruction quality.
1.1 HVQ
HVQ was proposed by Schneider and Westerman to improve the reconstruction quality of VQ[2,9–11]. Specifically, the volume data set is partitioned into separate blocks of size 43 initially. Then by down-sampling and difference calculation, each block is decomposed into a three-level representation, one mean level and two detail levels. An appropriate mapping and an associated codebook are produced for each detail level, by vector quantization. During quantization, by applying simple thresholding to each detail level, many difference vectors can be mapped to zero vector directly. In this way, the number of codewords used to present significant non-zero vectors can be maximized and further improve the fidelity. HVQ can obtain high reconstruction quality, however, sacrificing compression rate.
1.2 HVQ-1 d
Considering the significantly positive correlation between space environment variations in the same direction at two different scales, Bao et al. [1] had theoretically and experimentally proved the low utilization rate of codeword combinations and it is unnecessary to use two detail levels when HVQ is applied to space environment domain. Then Bao et al. [1] proposed HVQ-1 d which combines two detail levels in HVQ. By HVQ-1 d, each block of size 43 which is partitioned from the entire volume is decomposed to a mean value and a 64-component difference vector and presented as two levels, a mean level and a detail level. An appropriate vector quantizer is chosen and applied to the detail level, and each difference vector is replaced by the index in the codebook. Compared with HVQ, HVQ-1 d can achieve a higher compression rate and faster decoding speed without sacrificing fidelity.
Above methods only consider reducing the redundant information in a single volume of a specific variable. However, most space environment simulations produce multi-correlated variables at the same time. There are similar distribution patterns and variation characteristics among these variables. Therefore, this paper proposes HVQ-mv, which not only reduces the redundant information in a single volume of a variable, but also deals with the redundant information among these correlated variables.
2. Hierarchical Vector Quantization Based on Multi-correlated Variables
2.1 Basic Idea and Framework
Based on HVQ-1 d, our method further incorporates the compression among multi-correlated variables for space environment volume data. The framework of HVQ-mv is illustrated in Figure 1. Starting with space environment volume data and each voxel containing n correlated variable samples, the data associated with each variable is divided into disjoint blocks of size 43 initially. For each block, the difference between the mean value and original data samples is stored in a 64-component detail vector. The blocks are represented as two levels, a mean level and a detail level. The variable-specific mean values and detail vectors associated with n blocks at the same position are composited and stored in an n-component mean vector and a 64×n-component detail vector. In this way, variable-specific mean levels and detail levels are combined respectively to form a larger global mean level and a larger global detail level. By means of VQ, appropriate mappings and codebooks containing n- and 64×n-component codewords are generated for both global levels. LBG algorithm[12], as one of the most common vector quantization algorithms, is conducted for codebook refinement and quantization. A splitting based on a principal component analysis (PCA-split) is applied to compute initial codebooks for LBG.
Figure 1. Framework of HVQ-mv2.2 Compression
For a volume data set of size n×I×J×K (n variables, the volume of size I×J×K), assume that each sample is stored in B Byte, the indices into each codebook need 1 byte respectively, the length of each codebook is C, and each component in each codeword holds 1 Byte. The compression rate of HVQ-mv can be computed by
Rcompression=n×I×J×K×B2×I×J×K/43+C×n×64+C×n. (1) With the same codebook length, the compression rate of our method is significantly higher than that of HVQ and HVQ-1 d (for the compression rate of HVQ and HVQ-1 d refer to Referecnce [1,10]). Bits per voxel and can be computed by
Rbits/voxel=(2×I×J×K/43+C×n×64+C×n)×8I×J×K. (2) 2.3 Decompression and Rendering
The decompression is coupled with rendering on GPU. To reconstruct a sample for a specific variable, firstly get the indices of the block that contains the sample. Then look up the codebooks to obtain corresponding codewords according to the indices, and get the mean value and difference value with reference to the storage order of variables and relative positions in the block. Finally, add the mean value and difference value, and get the reconstructed value. Our method can support progressive rendering[1,7]. For real-time interactive volume visualization, during the interaction, we only use mean values to reconstruct an approximation for quick browsing, and when the interaction stops, we can fully reconstruct to reveal more details.
3. Results and Comparison
Solar Proton Events (SPE)[13] caused by solar activities are threats to space missions, because they can lead to the enhancement of high-energy radiation, furthermore affecting the condition of spacecraft and the safety of astronauts. Therefore, in the process of space missions, decision-makers need to comprehend the distribution of high-energy proton flux. Proton radiation simulation can generate several proton flux variables associated with different channels and these variables are positively correlated. Thus, we test our method along with HVQ and HVQ-1 d on high-energy proton flux data.
All experiments in this paper are compiled and run under Windows 10 on a 1.80 GHz Intel ® CoreTM i7-8550 U CPU with 20.0 GB main memory and an NVIDIA Quadro P500. The high-energy proton flux in the radiation belt at 00:00 UTC, 1 March 2022 is produced by AP8 model to test these methods and abbreviated as Proton Radiation Belt (PRB). The size of PRB is 4×200×200×100, 4 variables (> 5 MeV, > 10 MeV, > 30 MeV and > 50 MeV integrated proton flux) and the volume of size 200×200×100. The samples are scaled to 0~255 by normalization and each one is stored in 1 byte.
3.1 Compression Results and Comparison
As is common in compression, bits per voxel are used to measure the rate and Peak Signal-to-Noise Ratio (PSNR) to measure the distortion. The larger PSNR, the less distortion and the higher the reconstruction quality. the rate is varied by adjusting the sizes of codebooks. These results are shown in Figure 2.
Figure 2. Rate-distortion curves for all variables of PRB with HVQ, HVQ-1 d and HVQ-mv (Triangles label the points of HVQ, HVQ-1 d and HVQ-mv at rates 0.89, 0.88 and 0.78)The rate-distortion curve with HVQ-mv achieves an increase over HVQ-1 d. As we expect, HVQ-mv has an obvious quality advantage compared with HVQ-1 d, because it can reduce the redundancy information caused by the significant positive correlation among these variables. Correlation coefficients between > 10 and > 5, > 30, > 50 MeV flux are 0.92, 0.88, and 0.78 respectively. Both HVQ-mv and HVQ-1 d significantly outperform HVQ, because HVQ-mv and HVQ-1 d extra consider the spatial variation characteristics of the space environment[1]. For each curve, as the bits for each voxel increase, the reconstruction quality increases. When PSNR reaches 40.0 dB, the MSE is around 6.5. This paper further compares the reconstruction quality of HVQ, HVQ-1 d and HVQ-mv at rates 0.89, 0.88 and 0.78. The associated points are labeled as triangles in Figure 2, and Figure 3 to 6 illustrate the renderings of the corresponding compressed volumes.
Figure 3. Compression quality comparison of rendering > 5 MeV flux of PRB using HVQ, HVQ-1 d and HVQ-mv
Figure 4. Compression quality comparison of rendering > 10 MeV flux of PRB using HVQ, HVQ-1 d and HVQ-mv
Figure 5. Compression quality comparison of rendering > 30 MeV flux of PRB using HVQ, HVQ-1 d and HVQ-mv
Figure 6. Compression quality comparison of rendering > 50 MeV flux of PRB using HVQ, HVQ-1 d and HVQ-mvAs in Figure 2 and Figure 3 to 6, although the bits per voxel rate of HVQ-mv is lower than that of HVQ and that of HVQ-1 d, HVQ-mv achieves the best quality in all variables. Thus HVQ-mv pays the least cost of quality at compression. HVQ-1 d also still outperforms HVQ. The corresponding compression time is 6.27, 21.77 and 341.91 s for HVQ, HVQ-1 d and HVQ-mv respectively. The compression of HVQ-mv is the slowest, but that is acceptable since the compression is performed once offline[7].
3.2 Decompression and Rendering Results and Comparison
Rendering is applied directly from the compressed volumes based on GPU. All our examples are rendered using nearest neighbour interpolation, because linear interpolation within the codebook is not possible. Rendering results are referred to Figure 3 to 6. Frame rate is used to measure the rendering efficiency and the results are shown in Figure 7.
Figure 7. Efficiency comparison of rendering PRB directly from volumes compressed by HVQ, HVQ-1 d and HVQ-mvCompared with HVQ, both HVQ-mv and HVQ-1 d achieve higher frame rates due to fewer levels of representation and less dependent texture reads. The decompression and rendering speed of HVQ-mv is slightly lower than that of HVQ-1 d. Because HVQ-1 d can use the values in the mean level directly without the need to look up in a codebook.
During the interaction, we can only use mean values to reconstruct an approximation of HVQ-mv to speed up the rendering for quick browsing purposes and the frame rates are 36.0, 17.0 and 9.2 frame∙s–1 for screen sizes 512×512, 768×768, 1024×1024 pixel respectively. The rendering results are shown in Figure 8. The rendering for quick browsing is relatively lower quality. That is acceptable because we still can obtain the general distribution information and during interaction, speed is more important.
Figure 8. PRB rendering results of HVQ-mv quick browsingSimilar to proton radiation environment simulation, many other space environment simulations can also generate several correlated variables. For example, electron radiation environment simulation can generate several correlated electron flux variables associated with different channels, and atmosphere environment simulation can generate several correlated component variables. So the method proposed in this paper can also be employed for these environmental data. Furthermore, our method can be applied in other domains.
4. Conclusion
In this paper, based on HVQ-1 d we have further improved HVQ method for space environment volume data with multi-correlated variables, by reducing the redundancy information among these variables. With regard to performance, our method pays the least cost of quality at compression. Furthermore, a progressive rendering strategy has been adopted to decode and display the compressed volumes directly on GPU and this strategy can achieve satisfied reconstruction quality while ensuring an interactive rendering frame rate.
-
Figure 2. Rate-distortion curves for all variables of PRB with HVQ, HVQ-1 d and HVQ-mv (Triangles label the points of HVQ, HVQ-1 d and HVQ-mv at rates 0.89, 0.88 and 0.78)
Figure 3. Compression quality comparison of rendering > 5 MeV flux of PRB using HVQ, HVQ-1 d and HVQ-mv
Figure 4. Compression quality comparison of rendering > 10 MeV flux of PRB using HVQ, HVQ-1 d and HVQ-mv
Figure 5. Compression quality comparison of rendering > 30 MeV flux of PRB using HVQ, HVQ-1 d and HVQ-mv
Figure 6. Compression quality comparison of rendering > 50 MeV flux of PRB using HVQ, HVQ-1 d and HVQ-mv
Figure 7. Efficiency comparison of rendering PRB directly from volumes compressed by HVQ, HVQ-1 d and HVQ-mv
-
[1] BAO L L, CAI Y X, CUI Y M, et al. Compression and rendering of space environment volume data based on improved HVQ algorithm[J]. Journal of Physics:Conference Series, 2020, 1627: 012025 doi: 10.1088/1742-6596/1627/1/012025 [2] BAO L L, CAI Y X, LIN R L, et al. A weight based hierarchical vector quantization algorithm for space environment volume data[J]. Chinese Journal of Space Science, 2021, 41(3): 425-430 doi: 10.11728/cjss2021.03.425 [3] PIROTTI F, BROVELLI M A, PRESTIFILIPPO G, et al. An open source virtual globe rendering engine for 3 D applications: NASA world wind[J]. Open Geospatial Data, Software and Standards, 2017, 2: 4 doi: 10.1186/s40965-017-0016-5 [4] WANG S, WANG H Y, WU Y D, et al. Improved VolumeLIC rendering technology of 3 D vector field based on GPU acceleration[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(5): 723-732 [5] WANG C, ZHANG X G, XU X F, et al. The lunar and deep space environment exploration in China[J]. Journal of Deep Space Exploration, 2019, 6(2): 105-118 [6] WU Z B, YU J Q. Vector quantization: a review[J]. Frontiers of Information Technology & Electronic Engineering, 2019, 20(4): 507-524 [7] FOUT N, MA K L. Transform coding for hardware-accelerated volume rendering[J]. IEEE Transactions on Visualization and Computer Graphics, 2007, 13(6): 1600-1607 doi: 10.1109/TVCG.2007.70516 [8] NING P, HESSELINK L. Vector quantization for volume rendering[C]//Proceedings of 1992 Workshop on Volume Visualization. Boston: ACM, 1992: 69-74 [9] SCHNEIDER J, WESTERMANN R. Compression domain volume rendering[C]//Proceedings of IEEE Visualization. Seattle: IEEE, 2003: 293-300 [10] ZHAO L P, YUE G X, XIAO D G, et al. 2011 A content-based classified hierarchical vector quantization algorithm for volume compression[J]. Journal of Software, 2011, 6(2): 322-330 [11] YU S, ZHANG S Z, WANG K Q, et al. An efficient and fast GPU based algorithm for visualizing large volume of 4 D data from virtual heart simulations[J]. Biomedical Signal Processing and Control, 2017, 35: 8-18 doi: 10.1016/j.bspc.2017.01.015 [12] LINDE Y, BUZO A, GRAY R. An algorithm for vector quantizer design[J]. IEEE Transactions on Communications, 1980, 28(1): 84-95 doi: 10.1109/TCOM.1980.1094577 [13] MIAO J, LI Z T, REN T L, et al. Statistical analysis on four kinds of space weather events during solar cycles 21~24[J]. Chinese Journal of Space Science, 2021, 41(6): 849-857 doi: 10.11728/cjss2021.06.849 -
-
DownLoad:
下载:
计量
- 文章访问数: 285
- HTML全文浏览量: 122
- PDF下载量: 19
