基于参数自适应优化聚类的卫星状态异常检测方法

赵玉炜; 苏举

doi:10.11728/cjss2023.05.2022-0054

基于参数自适应优化聚类的卫星状态异常检测方法

doi: 10.11728/cjss2023.05.2022-0054 cstr: 32142.14.cjss2023.05.2022-0054

赵玉炜^{1, 2,},
苏举¹

1.
中国科学院国家空间科学中心　北京　100190
2.
中国科学院大学　北京　100049

基金项目: 中国科学院空间科学战略性先导科技专项项目资助（XDA15040100）

详细信息

作者简介:

赵玉炜：E-mail：zhaoyuwei21@mails.ucas.ac.cn

中图分类号: V474
计量
- 文章访问数: 626
- HTML全文浏览量: 101
- PDF下载量: 72
- 被引次数:
  0(来源:Crossref)
  
  0(来源:其他)
出版历程
- 收稿日期: 2022-09-21
- 修回日期: 2022-12-05
- 网络出版日期: 2023-06-25

Satellite Anomaly Detection Method Based on Parameter Adaptive Optimization Clustering

ZHAO Yuwei^{1, 2
,},
SU Ju¹

1.
National Space Science Center, Chinese Academy of Sciences, Beijing 100190
2.
University of Chinese Academy of Sciences, Beijing 100049

摘要

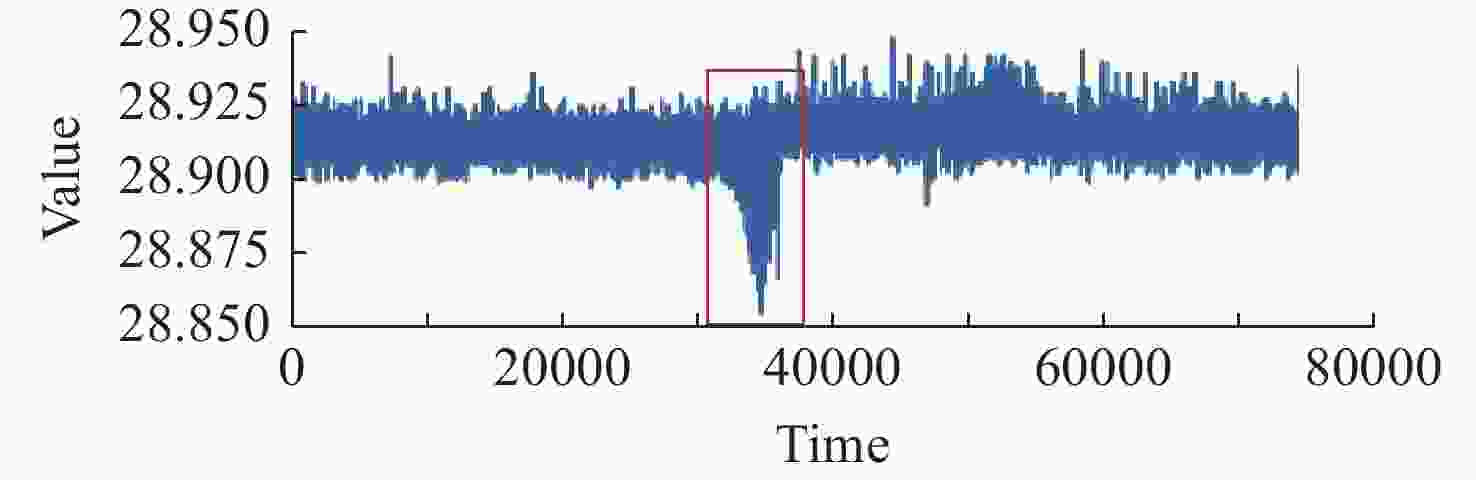
摘要: 对卫星在轨状态进行实时监测和异常检测，有利于保障卫星安全稳定运行。为解决在利用聚类分析检测卫星异常过程中，通过网格搜索选择最佳聚类超参数时精细度差、效率低的问题，本文将聚类超参数选择转化为单目标优化问题，并基于智能优化算法的启发式搜索能力，提出了超参数自适应优化的聚类算法UMOEAsII_BIRCH。为验证自适应搜索的有效性，在卫星遥测数据集和公开数据集上进行了测试。以网格搜索为基准，分别选取基于划分、基于密度和基于层次的聚类算法，对比自适应搜索和网格搜索两种方式下，异常检测的F1-score和算法执行时间。实验结果表明，自适应搜索克服了网格搜索中精细度与效率的矛盾，不受网格点的限制，异常检测效果优于基准方法，且在算法执行效率上具有显著优势。
- 遥测数据 /
- 异常检测 /
- 聚类分析 /
- 进化算法 /
- 网格搜索 /
- 参数自适应优化
Abstract: Real-time monitoring and anomaly detection of satellites in orbit are conducive to ensuring the safe and stable operation of satellites. In order to solve the problems of poor fineness, low efficiency and limited grid points when selecting the optimal clustering hyper-parameters through grid search in the process of detecting satellite anomalies using cluster analysis, the selection of clustering hyper-parameters is transformed into a single-objective optimization problem. And based on the heuristic search ability of intelligent optimization algorithm, a hyper-parameter adaptive optimization clustering algorithm UMOEAsII_BIRCH is proposed. To verify the effectiveness of adaptive search, tests are conducted on a satellite telemetry data set and a public data set. Using grid search as the benchmark, the clustering algorithms based on partition, density and hierarchy are selected respectively to compare the F1-score of anomaly detection and the algorithm execution time in adaptive search and grid search. The experimental results show that the proposed adaptive search overcomes the contradiction between fineness and efficiency in grid search, and is not limited by grid points. Besides, adaptive search outperforms grid search in the F1-score of anomaly detection, and has a significant advantage in execution efficiency.
- Telemetry data /
- Anomaly detection /
- Clustering analysis /
- Evolutionary algorithm /
- Grid search /
- Parameter adaptive optimization

HTML全文

图 1 单点异常示例

Figure 1. Example of point anomaly

下载: 全尺寸图片幻灯片

图 2 集体异常示例

Figure 2. Example of collective anomalies

下载: 全尺寸图片幻灯片

图 3 序列异常示例（绿色曲线为异常序列，黄色和蓝色曲线表示正常序列）

Figure 3. Example of sequential anomalies (Green represents the abnormal sequence, yellow and blue represent normal sequence)

下载: 全尺寸图片幻灯片

图 4 属性相关性热力图

Figure 4. Attribute correlation heat map

下载: 全尺寸图片幻灯片

图 5 异常点分布（蓝色表示正常点，红色表示异常点）

Figure 5. Distribution of anomalies (Blue represents normal points, and red represents abnormal points)

下载: 全尺寸图片幻灯片

图 6 进化算法演化过程曲线

Figure 6. Evolution process curve of evolutionary algorithm

下载: 全尺寸图片幻灯片

图 7 参数网格搜索过程

Figure 7. Process of parameter grid searching

下载: 全尺寸图片幻灯片

表 1 混淆矩阵

Table 1. Confusion matrix

		预测类别
		正例	负例
真实类别	正例	TP	FN
真实类别	负例	FP	TN

下载: 导出CSV

表 2 UMOEAs-II算法参数设置

Table 2. Parameter settings of UMOEAs-II

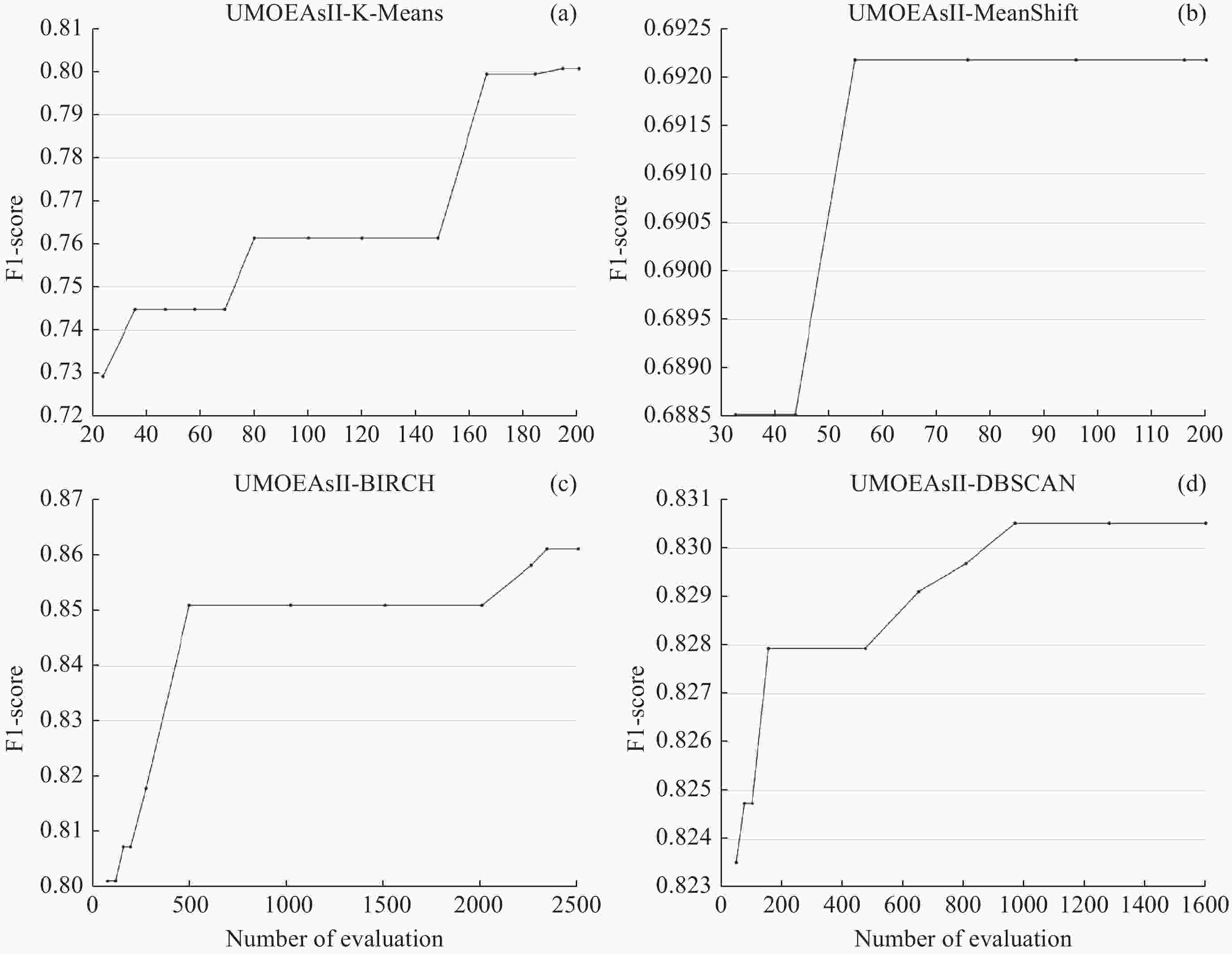
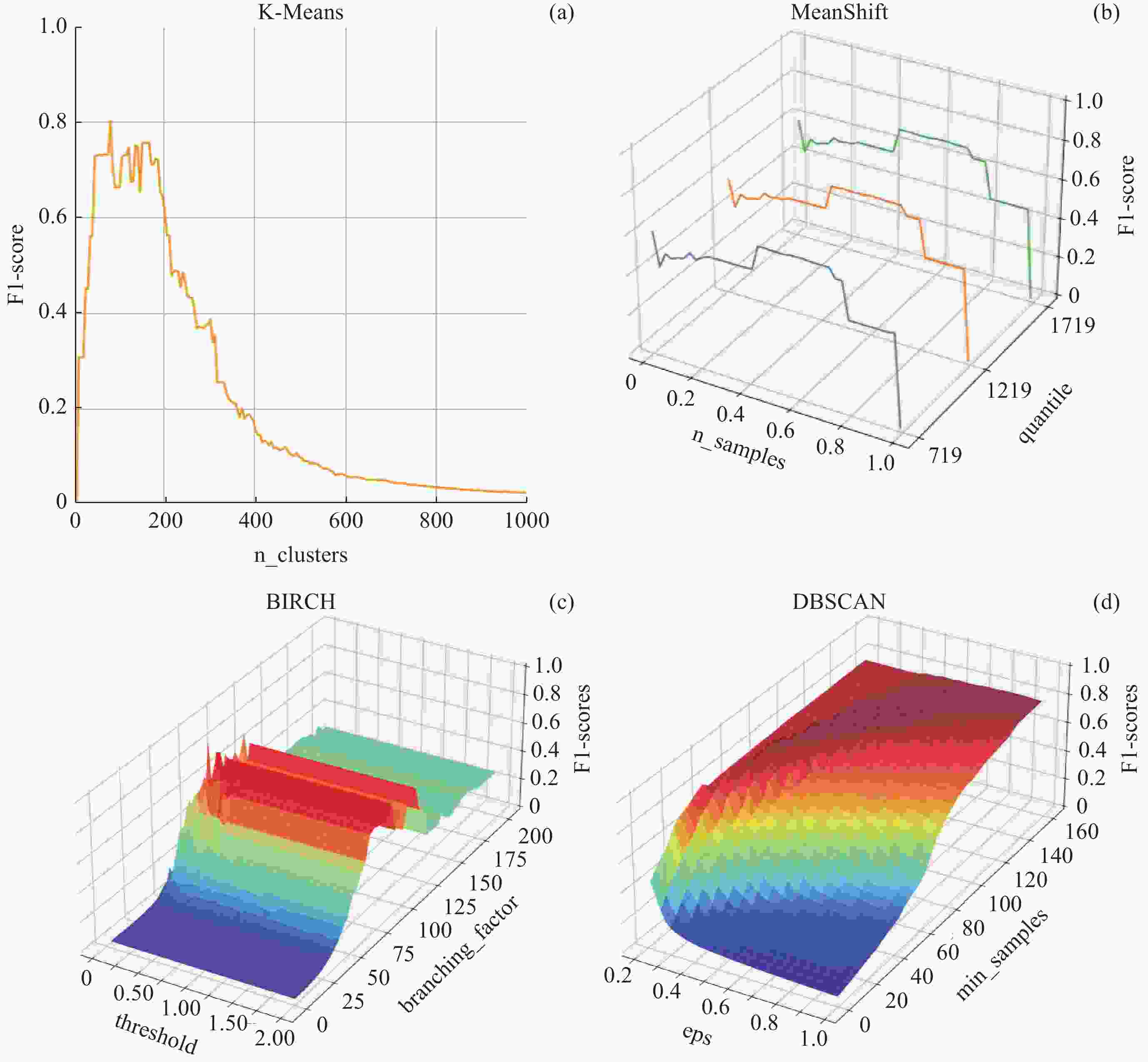
	最大评估次数	种群大小	问题维度	超参数名称	超参数取值范围
UMOEAsII_MeanShift	120	5	2	quantile	[0.01, 1.0]
UMOEAsII_MeanShift	120	5	2	n_samples	[500, 2000]
UMOEAsII_K-Means	200	8	1	n_clusters	[2, 1000]
UMOEAsII_DBSCAN	1600	22	2	eps	[0.2, 1.0]
UMOEAsII_DBSCAN	1600	22	2	min_samples	[2, 160]
UMOEAsII_BIRCH	2500	36	2	threshold	[0.001, 2.0]
UMOEAsII_BIRCH	2500	36	2	branching_factor	[2, 200]
注　问题维度，代表聚类算法要寻优的超参数个数。

下载: 导出CSV

表 3 网格搜索测试参数组合

Table 3. Parameter combinations of grid search

算法名称	超参数名称	超参数取值范围	搜索步长	网格点数
MeanShift	quantile	（0.001, 1.0）	0.025	120
MeanShift	n_samples	（500, 2000）	500	120
K-Means	n_clusters	（2, 1000）	5	200
DBSCAN	eps	（0.2, 1.0）	0.02	1600
DBSCAN	min_samples	（2, 160）	4	1600
BIRCH	threshold	（0.001, 2.0）	0.04	2500
BIRCH	branching_factor	（2, 200）	4	2500

下载: 导出CSV

表 4 算法测试结果对比

Table 4. Comparison of algorithm test results

	F1-score 最优值	F1-score 最差值	F1-score 均值	F1-score 方差	算法执行时间/s
MeanShift	0.6922	0.6922	0.6922	0.00000	4780
UMOEAsII_MeanShift	0.6922	0.6922	0.6922	0.00000	4087
K-Means	0.8006	0.7545	0.7871	0.01994	156639
UMOEAsII_K-Means	0.8006	0.7650	0.7969	0.01066	104939
DBSCAN	0.8297	0.8277	0.8286	0.00066	502272
UMOEAsII_DBSCAN	0.8305	0.8294	0.8298	0.00039	394553
BIRCH	0.8519	0.7734	0.8191	0.02580	172106
UMOEAsII_BIRCH	0.8610	0.8542	0.8568	0.00205	86930
注　加粗数据表示最优结果。

下载: 导出CSV

表 5 UMOEAs-II算法参数设置

Table 5. Parameter settings of UMOEAs-II

	最大评估次数	种群大小	问题维度	超参数名称	超参数取值范围
UMOEAsII_K-Means	200	8	1	n_clusters	[2, 1000]
UMOEAsII_DBSCAN	1200	22	2	eps	[0.1, 1.0]
UMOEAsII_DBSCAN	1200	22	2	min_samples	[2, 160]
UMOEAsII_BIRCH	1600	24	2	threshold	[0.001, 2.0]
UMOEAsII_BIRCH	1600	24	2	branching_factor	[2, 200]

下载: 导出CSV

表 6 网格搜索测试参数组合

Table 6. Parameter combinations of grid search

算法名称	超参数名称	超参数取值范围	搜索步长	网格点数
K-Means	n_clusters	（2, 1000）	5	200
DBSCAN	eps	（0.1, 1.0）	0.03	1200
DBSCAN	min_samples	（2, 160）	4	1200
BIRCH	threshold	（0.001, 2.0）	0.05	1600
BIRCH	branching_factor	（2, 200）	5	1600

下载: 导出CSV

表 7 算法测试结果

Table 7. Algorithm test results

	F1-score 最优值	F1-score 最差值	F1-score 均值	F1-score 方差	算法执行时间/s
K-Means	0.5965	0.5348	0.5674	2.6505×10^–2	1091.75
UMOEAsII_K-Means	0.5965	0.5965	0.5965	2.3406×10^–16	681.86
DBSCAN	0.4639	0.4470	0.4571	4.7600×10^–3	1443.58
UMOEAsII_DBSCAN	0.4671	0.4671	0.4671	4.6800×10^–16	1299.00
BIRCH	0.6139	0.4865	0.5379	3.8275×10^–2	2944.44
UMOEAsII_BIRCH	0.6415	0.6415	0.6415	0.0000	1351.90
注　加粗数据表示最优结果。

下载: 导出CSV

参考文献(17)

[1]	PAN D W, LIU D T, ZHOU J, et al. Anomaly detection for satellite power subsystem with associated rules based on Kernel Principal Component Analysis[J]. Microelectronics Reliability, 2015, 55(9/10): 2082-2086
[2]	ZHENG L, GUANG J, TANG S H. Fluctuation feature extraction of satellite telemetry data and on-orbit anomaly detection[C]//2016 Prognostics and System Health Management Conference. Chengdu: IEEE, 2017: 1-5
[3]	赵佳, 吕弘, 刘宝, 等. 基于模糊Petri网的卫星导航接收系统故障诊断[J]. 测试技术学报, 2017, 31(5): 438-442 ZHAO Jia, LV Hong, LIU Bao, et al. Fault diagnosis for GNSS receiver based on fuzzy Petri Net[J]. Journal of Test and Measurement Technology, 2017, 31(5): 438-442
[4]	张怀峰, 江婧, 张香燕, 等. 面向卫星电源系统的一种新颖异常检测方法[J]. 宇航学报, 2019, 40(12): 1468-1477 doi: 10.3873/j.issn.1000-1328.2019.12.011 ZHANG Huaifeng, JIANG Jing, ZHANG Xiangyan, et al. Novel anomaly detection method for satellite power system[J]. Journal of Astronautics, 2019, 40(12): 1468-1477 doi: 10.3873/j.issn.1000-1328.2019.12.011
[5]	李钰骙, 李虎, 胡钛. 基于LightGBM的HXMT在轨运行模式监测算法[J]. 空间科学学报, 2020, 40(1): 109-116 doi: 10.11728/cjss2020.01.109 LI Yukui, LI Hu, HU Tai. In-orbit operational pattern monitoring algorithms based on LightGBM for Hard X-ray Modulation Telescope Satellite[J]. Chinese Journal of Space Science, 2020, 40(1): 109-116 doi: 10.11728/cjss2020.01.109
[6]	李虎, 郭国航, 胡钛, 等. 遥测参数数据载荷状态判别集成学习方法[J]. 国防科技大学学报, 2021, 43(6): 33-40 LI Hu, GUO Guohang, HU Tai, et al. Ensemble learning for state recognition of payload from telemetry data[J]. Journal of National University of Defense Technology, 2021, 43(6): 33-40
[7]	CASAS P, MAZEL J, OWEZARSKI P. UNADA: unsupervised network anomaly detection using sub-space outliers ranking[C]//Proceedings of the 10 th International Conference on Research in Networking. Valencia: Springer, 2011: 40-51
[8]	陆春光, 叶方彬, 赵羚, 等. 基于密度峰值聚类的电力大数据异常值检测算法[J]. 科学技术与工程, 2020, 20(2): 654-658 LU Chunguang, YE Fangbin, ZHAO Ling, et al. Abnormal value detection of large power data based on density peak clustering[J]. Science Technology and Engineering, 2020, 20(2): 654-658
[9]	WANG H, PENG M J, YU Y, et al. Fault identification and diagnosis based on KPCA and similarity clustering for nuclear power plants[J]. Annals of Nuclear Energy, 2021, 150: 107786 doi: 10.1016/j.anucene.2020.107786
[10]	李楠, 强懿耕, 樊瑞, 等. 基于异常因子的航空器飞行轨迹异常检测研究[J]. 安全与环境学报, 2021, 21(2): 643-648 LI Nan, QIANG Yigeng, FAN Rui, et al. On the abnormal detection of the aircraft flight trajectory based on the abnormal factor statistics[J]. Journal of Safety and Environment, 2021, 21(2): 643-648
[11]	彭喜元, 庞景月, 彭宇, 等. 航天器遥测数据异常检测综述[J]. 仪器仪表学报, 2016, 37(9): 1929-1945 PENG Xiyuan, PANG Jingyue, PENG Yu, et al. Review on anomaly detection of spacecraft telemetry data[J]. Chinese Journal of Scientific Instrument, 2016, 37(9): 1929-1945
[12]	康旭. 时序遥测数据异常检测方法研究[D]. 南京: 南京航空航天大学, 2018 KANG Xu. Anomaly Detection Method for Sequential Telemetry Data[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018
[13]	ZHANG T, RAMAKRISHNAN R, LIVNY M. BIRCH: An efficient data clustering method for very large databases[J]. ACM SIGMOD Record, 1999, 25(2): 103-114
[14]	陈婧文. 基于链接改进的BIRCH算法的研究与应用[D]. 长春: 吉林大学, 2019 CHEN Jingwen. Research and Application of an Improved BIRCH Algorithm Based on Link[D]. Changchun: Jilin University, 2019
[15]	ELSAYED S, HAMZA N, SARKER R. Testing united multi-operator evolutionary algorithms-II on single objective optimization problems[C]//2016 IEEE Congress on Evolutionary Computation (CEC). Vancouver: IEEE, 2016: 2966-2973
[16]	ELSAYED S M, SARKER R A, ESSAM D L, et al. Testing united multi-operator evolutionary algorithms on the CEC2014 real-parameter numerical optimization[C]//2014 IEEE Congress on Evolutionary Computation (CEC). Beijing: IEEE, 2014: 1650-1657
[17]	HRUSCHKA E R, CAMPELLO R J G B, FREITAS A A, et al. A survey of evolutionary algorithms for clustering[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2009, 39(2): 133-155 doi: 10.1109/TSMCC.2008.2007252