Wave Propagation Law at the Gas-liquid Interface in a Storage Tank Due to Gravity Jumps
-
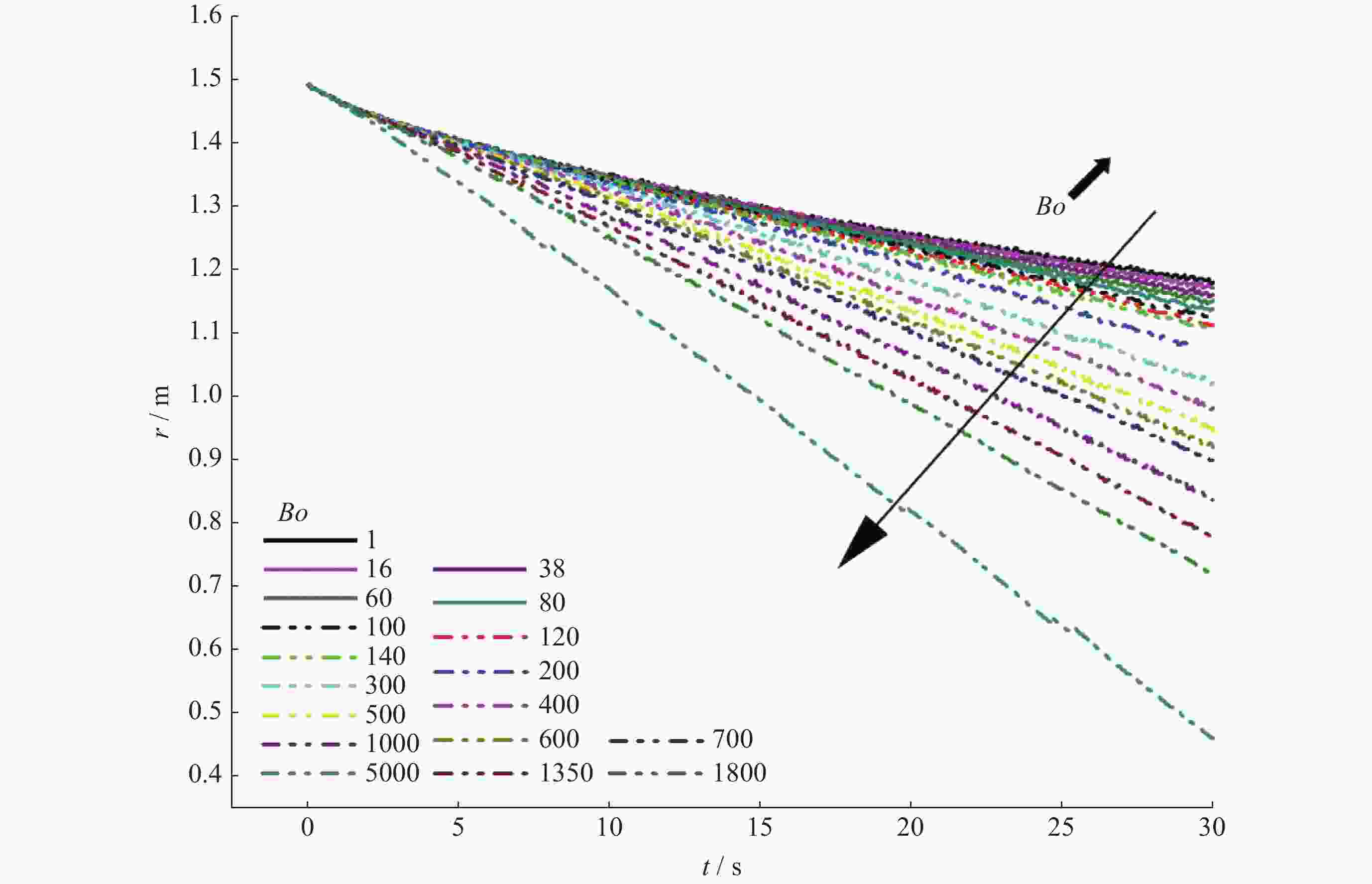
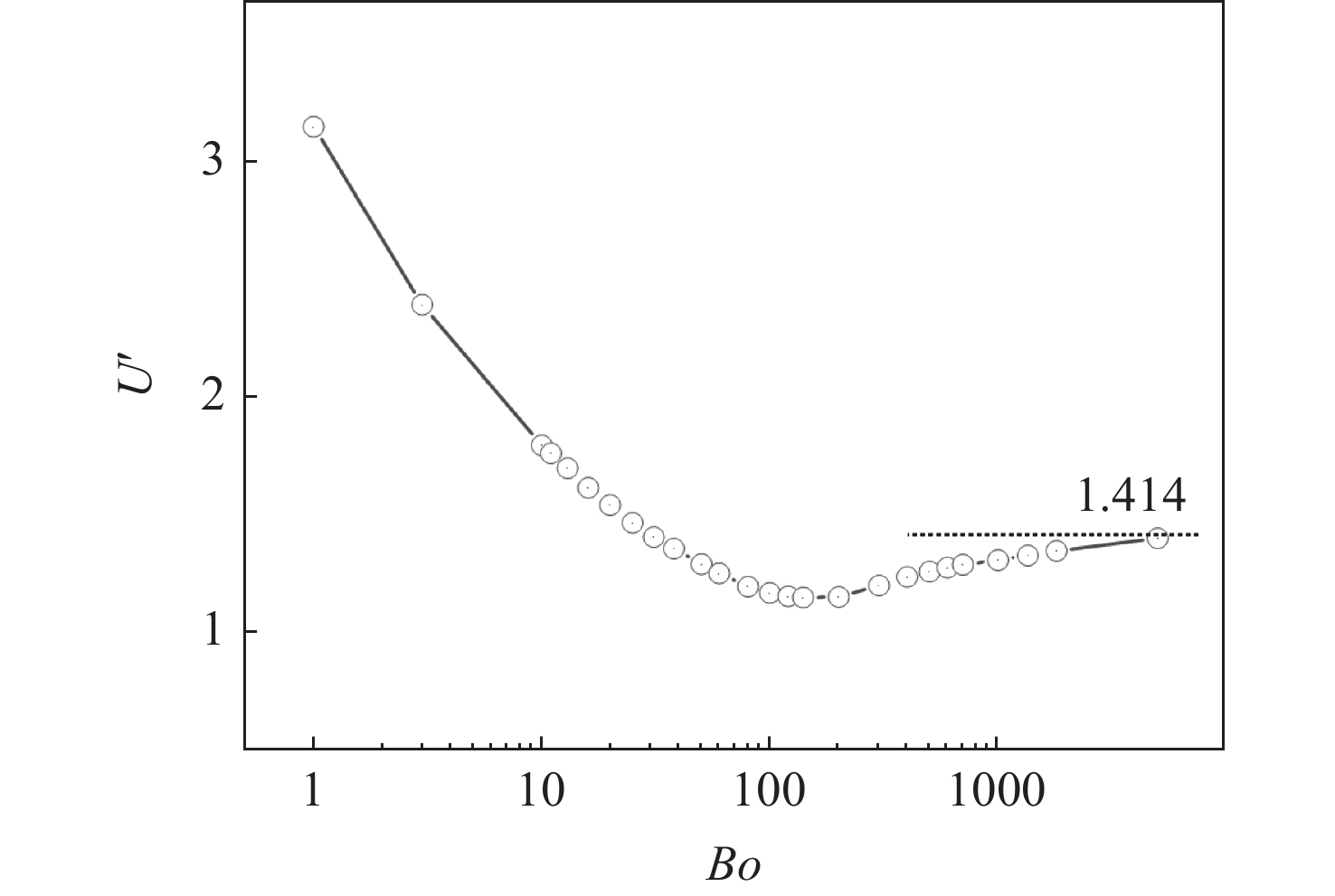
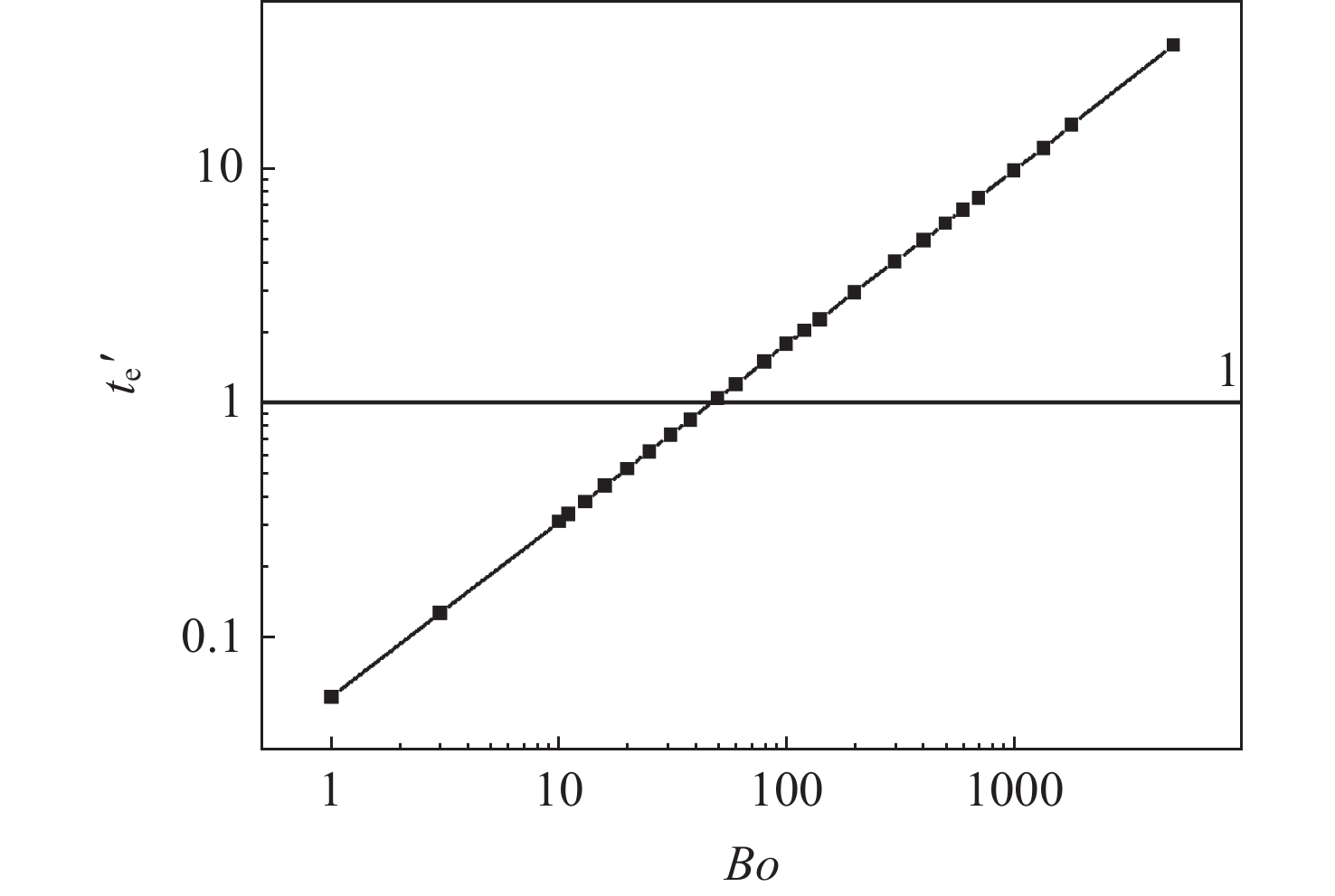
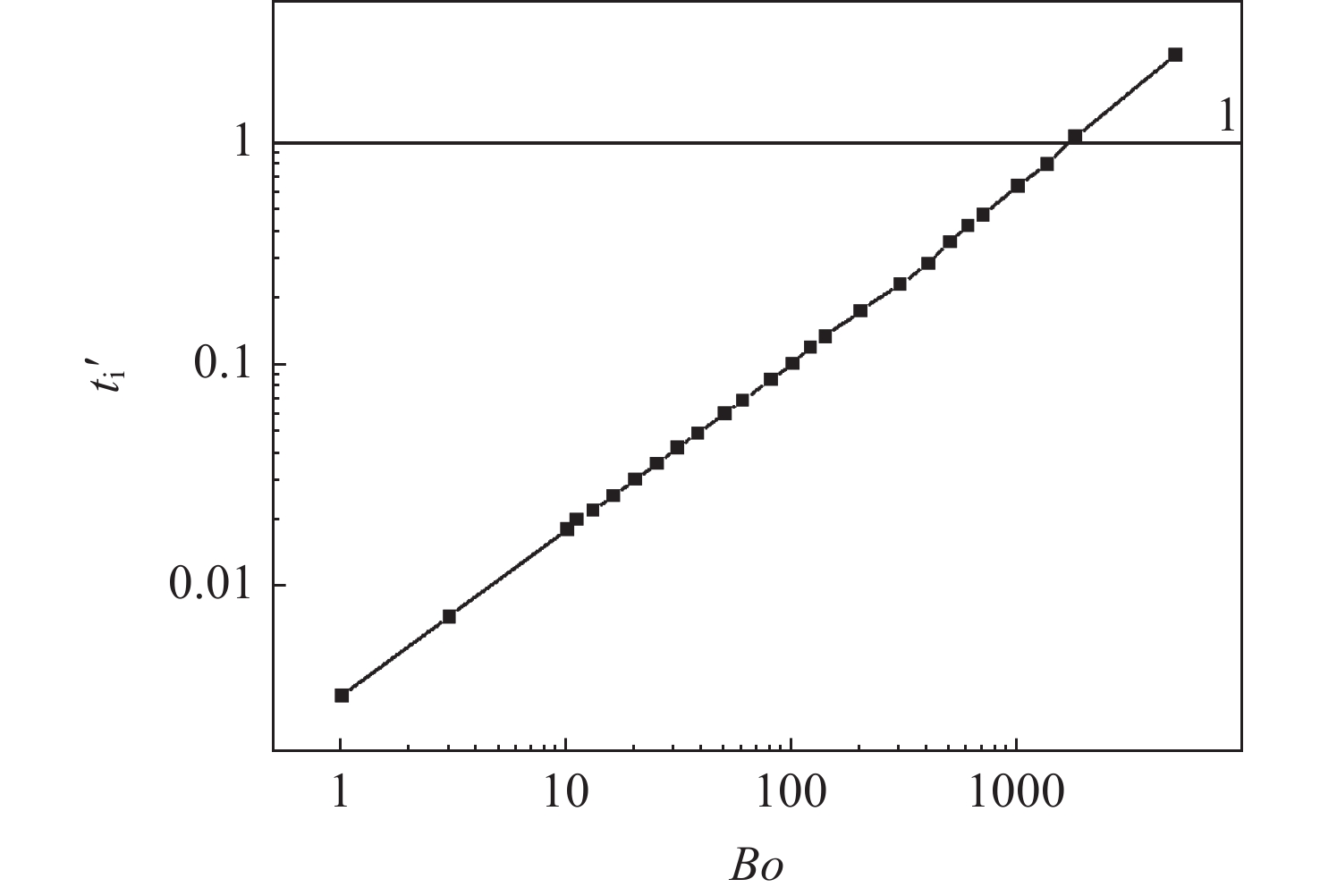
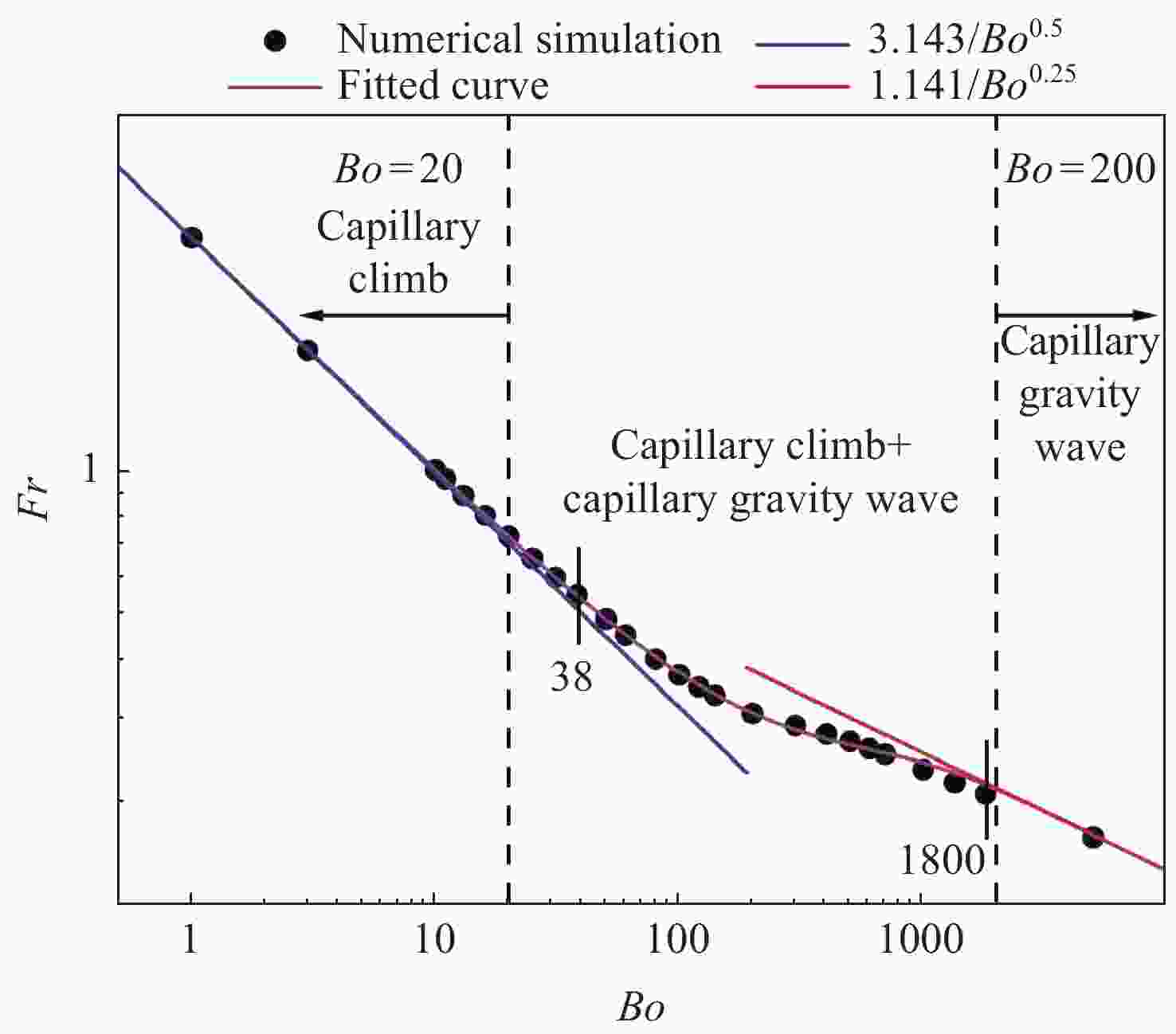
摘要: 随着航天技术的进步，航天任务复杂性的不断提高，对液体火箭发动机多次关机重启的要求日益普遍，相应地对推进剂管理系统的要求也越来越严格。关机滑行期间，贮箱内重力水平减弱，毛细力开始成为主导作用力，液体推进剂在毛细力的作用下可能脱离排液口，使得供给发动机的推进剂夹气，导致点火失败。为了确保发动机在经历自由滑行后能顺利重启，就必须考虑贮箱内气液界面如何响应重力和加速度水平改变的问题。针对常用构型和尺寸的空间贮箱，数值模拟了不同Bo数下气液界面波的传播，研究了不同Bo数下界面波传播的机制，发现了贮箱内界面波的传播速度随着Bo数的增加而增大，并得到Bo数从1～5000范围内描述界面波传播规律的Fr数与Bo数之间的标度关系。Abstract: With the advancement of aerospace technology and the increasing complexity of space exploration missions, it is increasingly common to require multiple shutdowns and restarts of liquid rocket engines, and correspondingly, the requirements for propellant management systems are becoming increasingly rigorous. During shutdown coasting, the level of gravity in the reservoir decreases and capillary forces begin to dominate. The liquid propellant may break away from the discharge port under the capillary force, which allows the propellant supplied to the engine to entrap gas, resulting in ignition failure. To ensure that the engine can be restarted after experiencing free flight, it is necessary to consider how the gas-liquid interface inside the propellant tank responds to gravity and acceleration jumps. In this paper, the propagation of gas-liquid interfacial wave under different values of the Bond number is numerically simulated for commonly used configurations and sizes of space propellant tanks, and the mechanism of the propagation of interfacial wave under different values of the Bond number is investigated. Finally, It is found that the propagation velocity of interfacial waves in a storage tank increases with the Bond number, and the scaling law between the Froude number and the Bond number in the range of the Bo numbers from 1 to 5000 is obtained to characterize the propagation of interfacial wave.
-
图 2 Bo=200时初始界面波的移动（虚线箭头表示近壁波谷）
Figure 2. Displacement of the main wave trough at Bo = 200 (Dashed arrow indicates near-wall troughs)
图 3 不同Bo数下初始波谷位置的变化
Figure 3. Movement of the initial trough of interface wave under different values of the Bond number
图 4 不同Bo数下界面波的无量纲传播速度变化情况
Figure 4. Change of the dimensionless propagation velocity of the interface wave under different values of the Bond number
图 5 不同Bo数下界面波自由传播的无量纲终止时刻
Figure 5. Dimensionless termination moments of free propagation of interface waves for different Bo numbers
图 6 不同Bo数下界面波自由传播的无量纲初始时刻
Figure 6. Dimensionless initial moments of free propagation of interface waves for different Bo numbers
图 7 Fr数与Bo数之间的标度关系
Figure 7. Scaling relationship between the Fr number and Bo numbers
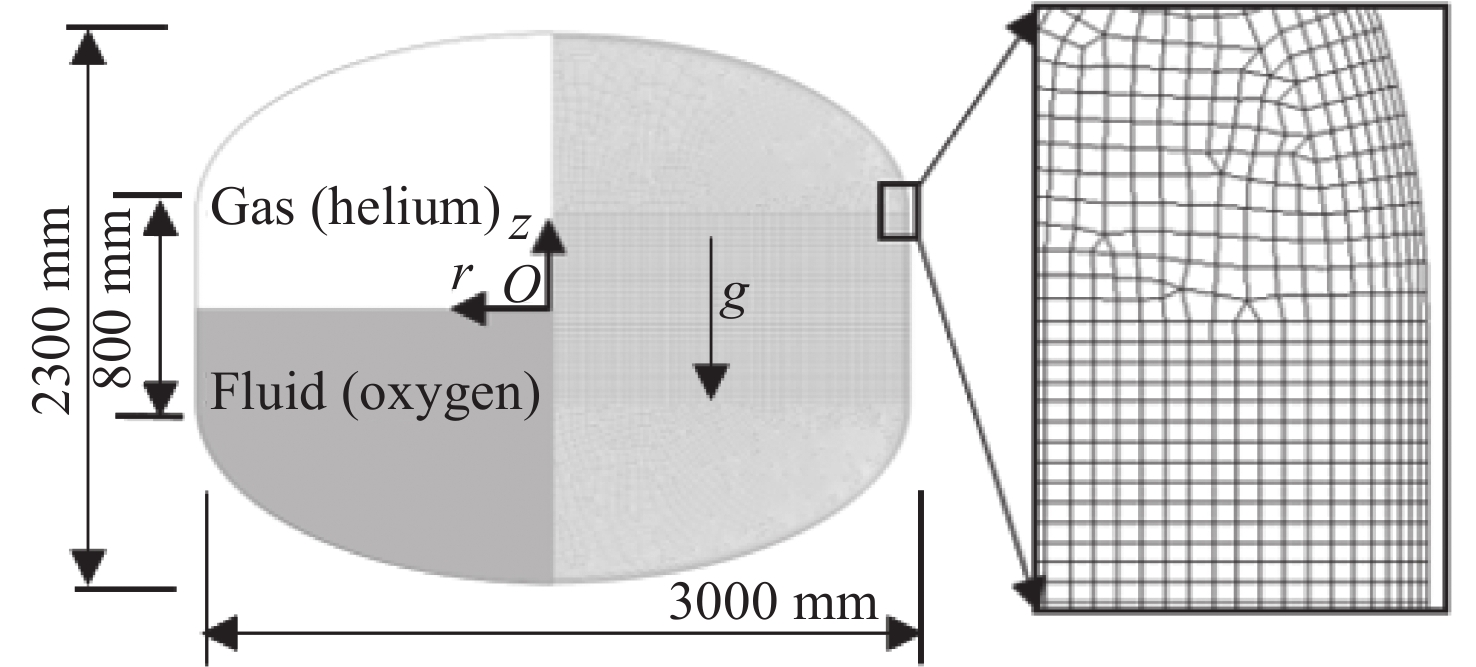
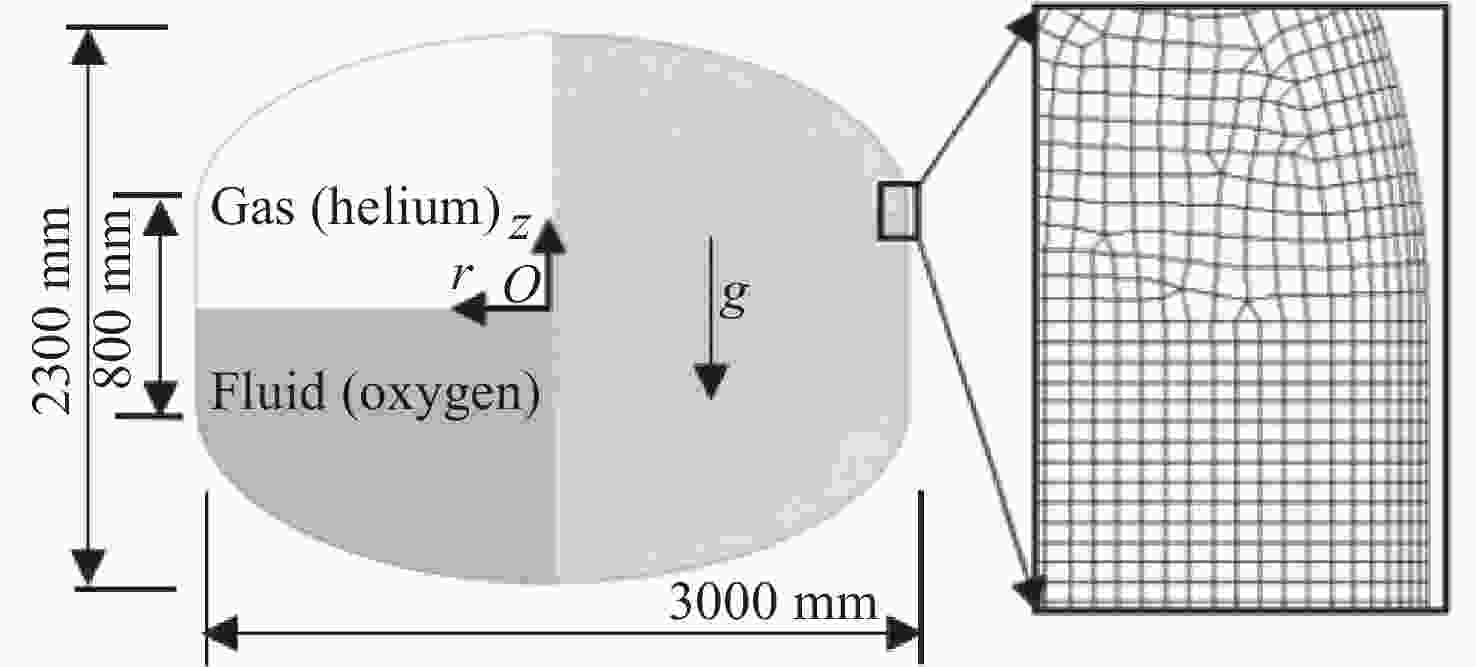
表 1 气液两相流体物性参数
Table 1. Material parameters of the gas and liquid phases
Fluid materials Helium (Gas) Oxygen (Liquid) Density/(kg·m–3) 1.230 1200 Dynamic viscosity/(μPa·s) 8.385 279.1 Surface tension/(N·m–1) 0.0162 Contact angle/(°) 10 
下载: 导出CSV
-
[1] KARTUZOVA O V, KASSEMI M. CFD jet mixing model validation against Zero-Boil-Off tank (ZBOT) microgravity experiment[C]//Proceedings of the AIAA Propulsion and Energy 2019 Forum. Indianapolis: American Institute of Aeronautics and Astronautics, 2019 [2] 郭斌, 赵建福, 李凯, 等. 零重力条件下低温射流抑制大尺寸液氢储罐热分层的数值研究[J]. 力学学报, 2021, 53(4): 1170-1182 doi: 10.6052/0459-1879-20-343GUO Bin, ZHAO Jianfu, LI Kai, et al. Numerical study on thermal destratification in large scale hydrogen propellant tank in space by jet injection under zero gravity condition[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(4): 1170-1182 doi: 10.6052/0459-1879-20-343 [3] LI J C, GUO B, ZHAO J F, et al. On the space thermal destratification in a partially filled hydrogen propellant tank by jet injection[J]. Microgravity Science and Technology, 2022, 34(1): 6 doi: 10.1007/s12217-021-09923-2 [4] 肖立明, 李欣, 胡声超, 等. 微重力条件下上面级贮箱液体推进剂自由界面变形数值模拟研究[J]. 航天器环境工程, 2020, 37(2): 115-119 doi: 10.12126/see.2020.02.002XIAO Liming, LI Xin, HU Shengchao, et al. Numerical simulation of free interface deformation of liquid propellant in upper stage tank under microgravity condition[J]. Spacecraft Environment Engineering, 2020, 37(2): 115-119 doi: 10.12126/see.2020.02.002 [5] MASICA W J, PETRASH D A. Motion of Liquid-Vapor Interface in Response to Imposed Acceleration[R]. Washington: NASA, 1965 [6] MASICA W J, PETRASH D A, OTTO E W. Hydrostatic Stability of the Liquid-Vapor Interface in a Gravitational Field[R]. Washington: NASA, 1964 [7] MASICA W J, DERDUL J D, PETRASH D A. Hydrostatic Stability of the Liquid-Vapor Interface in A Low-Acceleration Field[R]. Washington: NASA, 1964 [8] BRETHERTON F P. The motion of long bubbles in tubes[J]. Journal of Fluid Mechanics, 1961, 10(2): 166-188 doi: 10.1017/S0022112061000160 [9] GLUCK D F, GILLE J P. Fluid mechanics of zero-G propellant transfer in spacecraft propulsion systems[J]. Journal of Engineering for Industry, 1965, 87(1): 1-8 doi: 10.1115/1.3670751 [10] ABRAMSON H N. The Dynamic Behavior of Liquids in Moving Containers[R]. Washington: NASA, 1966 [11] WEISLOGE M M, HSIEH K C. Stability of Capillary Surfaces in Rectangular Containers: The Right Square Cylinder[R]. Washington: NASA, 1998 [12] DAVIES R M, TAYLOR G I. The mechanics of large bubbles rising through extended liquids and through liquids in tubes[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 1950, 200(1062): 375-390 [13] BERRY R L, TEGART J R. Experimental Study of Transient Liquid Motion in Orbiting Spacecraft[R]. Washington: NASA, 1975 [14] LABUS T L, MASICA W J. Liquid Reorientation in Spheres by Means of Low-G Accelerations[R]. Washington: NASA, 1968 [15] SALZMAN J A, MASICA W J. Experimental Investigation of Liquid-Propellant Reorientation[R]. Washington: NASA, 1967 [16] SALZMAN J A, MASICA W J, LACOVIC R F. Low Gravity Reorientation in A Scale-Model Centaur Liquid-Hydrogen Tank[R]. Washington: NASA, 1973 [17] HOCHSTEIN J I, PATAG A E, CHATO D J. Modeling of Impulsive Propellant Reorientation[R]. Washington: NASA, 1989 [18] PATAG A E, HOCHSTEIN J I, CHATO D J. Modeling of pulsed propellant reorientation[C]//Proceedings of the 25 th Joint Propulsion Conference. Monterey: American Institute of Aeronautics and Astronautics, 1989 [19] HOCHSTEIN J I, PATAG A E, KORAKIANITIS T P, et al. Pulsed thrust propellant reorientation: concept and modeling[J]. Journal of Propulsion and Power, 1992, 8(4): 770-777 doi: 10.2514/3.23548 [20] CONCUS P. Static menisci in a vertical right circular cylinder[J]. Journal of Fluid Mechanics, 1968, 34(3): 481-495 doi: 10.1017/S002211206800203X [21] PETRASH D A, NELSON T M, OTTO E W. Effect of Surface Energy on the Liquid-Vapor Interface Configuration During Weightlessness[R]. Washington: NASA, 1963 [22] SIEGERT C E, PETRASH D A, OTTO E W. Time Response of Liquid-Vapor Interface After Entering Weightlessness[R]. Washington: NASA, 1964 [23] HOCKING L M. The damping of capillary–gravity waves at a rigid boundary[J]. Journal of Fluid Mechanics, 1987, 179: 253-266 doi: 10.1017/S0022112087001514 [24] KAUKLER W F. Fluid oscillation in the drop tower[J]. Metallurgical Transactions A, 1988, 19(11): 2625-2630 doi: 10.1007/BF02645793 [25] WOLK G, DREYER M, RATH H J, et al. Damped oscillations of a liquid/gas surface upon step reduction in gravity[J]. Journal of Spacecraft and Rockets, 1997, 34(1): 110-117 doi: 10.2514/2.3179 [26] MICHAELIS M, DREYER M E, RATH H J. Experimental investigation of the liquid interface reorientation upon step reduction in gravity[J]. Annals of the New York Academy of Sciences, 2002, 974(1): 246-260 doi: 10.1111/j.1749-6632.2002.tb05911.x [27] MICHAELIS M, GERSTMANN J, DREYER M E, et al. Damping behavior of the free liquid interface oscillation upon step reduction in gravity[J]. Proceedings in Applied Mathematics and Mechanics, 2003, 2(1): 320-321 doi: 10.1002/pamm.200310144 [28] STIEF M, DREYER M. Experimental investigation of surface reorientation and oscillations of liquid nitrogen[C]//Proceedings of the 56 th International Astronautical Congress of the International Astronautical Federation, the International Academy of Astronautics, and the International Institute of Space Law. Fukuoka: American Institute of Aeronautics and Astronautics, 2005 [29] LI J C, LIN H, ZHAO J F, et al. Dynamic behaviors of liquid in partially filled tank in short-term microgravity[J]. Microgravity Science and Technology, 2018, 30(6): 849-856 doi: 10.1007/s12217-018-9642-5 [30] LI J C, LIN H, LI K, et al. Liquid sloshing in partially filled capsule storage tank undergoing gravity reduction to low/micro-gravity condition[J]. Microgravity Science and Technology, 2020, 32(4): 587-596 doi: 10.1007/s12217-020-09801-3 [31] LI J C, LIN H, LI K, et al. Dynamic behavior in a storage tank in reduced gravity using dynamic contact angle method[J]. Microgravity Science and Technology, 2020, 32(6): 1039-1048 doi: 10.1007/s12217-020-09831-x [32] 魏列, 杜王芳, 赵建福, 等. 微重力条件下部分充液贮箱气液界面波动特性的数值模拟[J]. 力学学报, 2022, 54(4): 1004-1011 doi: 10.6052/0459-1879-21-645WEI Lie, DU Wangfang, ZHAO Jianfu, et al. Numerical study on gas-liquid interface waves in partially filled tanks under microgravity condition[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(4): 1004-1011 doi: 10.6052/0459-1879-21-645 [33] HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225 doi: 10.1016/0021-9991(81)90145-5 [34] BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354 doi: 10.1016/0021-9991(92)90240-Y [35] WEISLOGEL M M. Fluid interface phenomena in a low-gravity environment: recent results from drop tower experimentation[J]. Space Forum, 1998, 3: 59-86 [36] 庄礼贤, 尹协远, 马晖扬. 流体力学[M]. 2版. 合肥: 中国科学技术大学出版社, 2009ZHUANG Lixian, YIN Xieyuan, MA Huiyang. Fluid Mechanics[M]. 2 nd ed. Hefei: University of Science and Technology of China Press, 2009 -
-
下载:
图(7) / 表(1)
计量
- 文章访问数: 175
- HTML全文浏览量: 88
- PDF下载量: 29
-
被引次数:
0(来源:Crossref)
0(来源:其他)
