基于中法海洋卫星波谱仪观测的一维海浪谱模型对比
doi: 10.11728/cjss2023.06.2023-0068 cstr: 32142.14.cjss2023.06.2023-0068
Comparisons on One-dimensional Ocean Wave Spectrum Models Based on SWIM/CFOSAT Observations
-
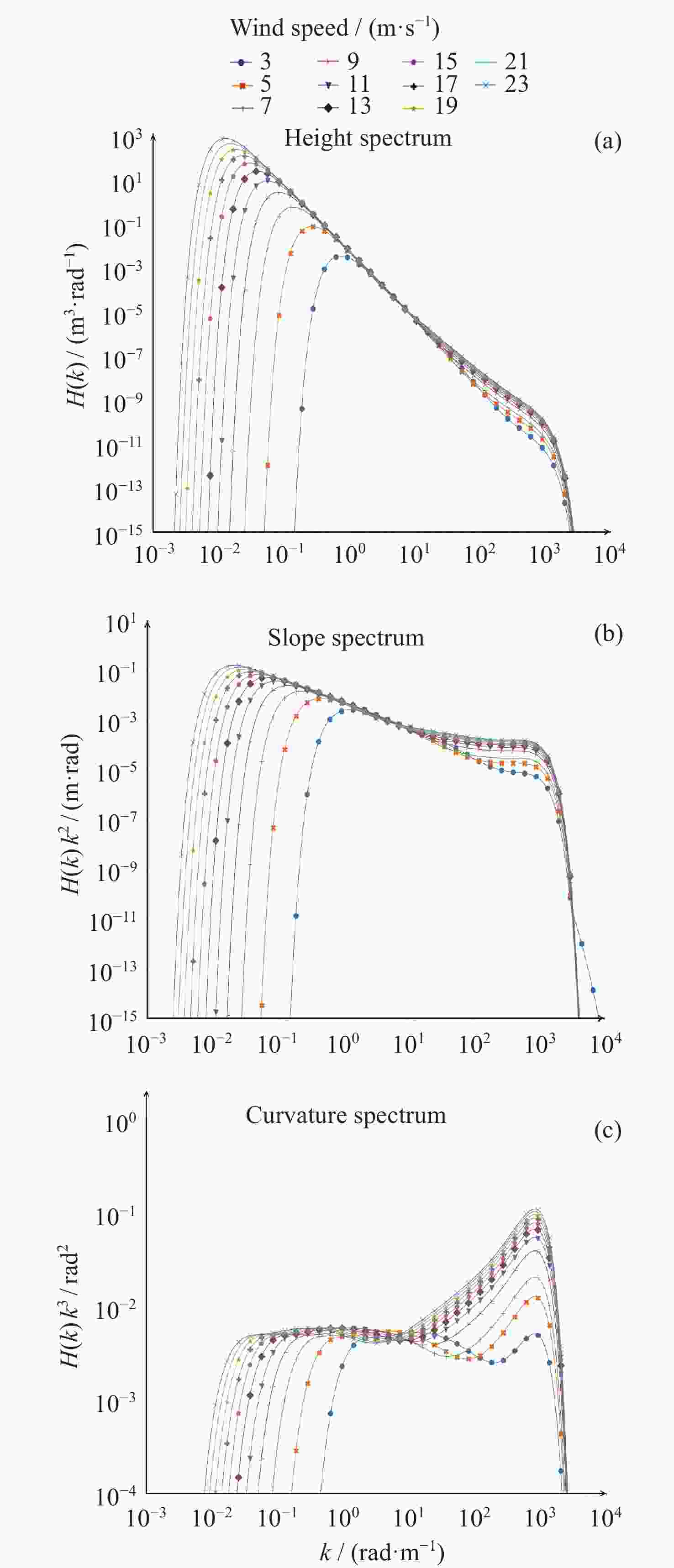
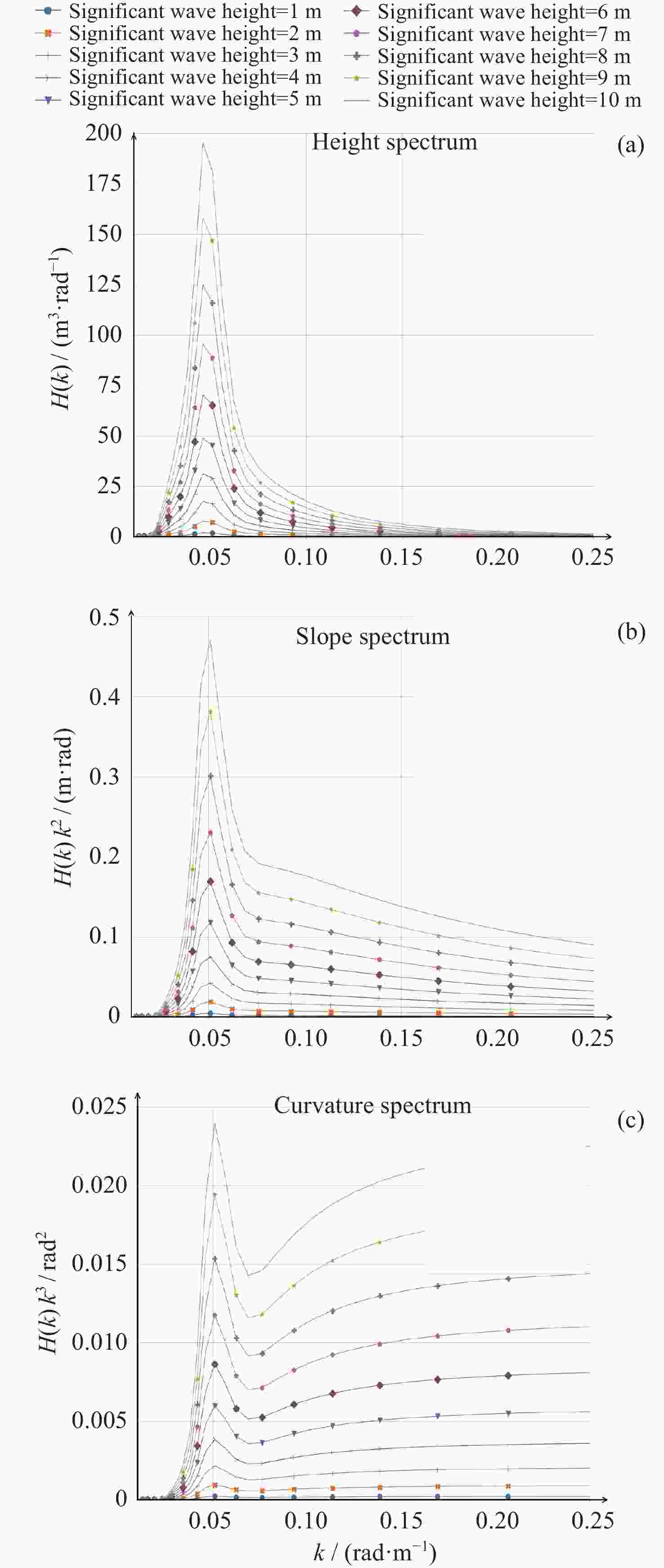
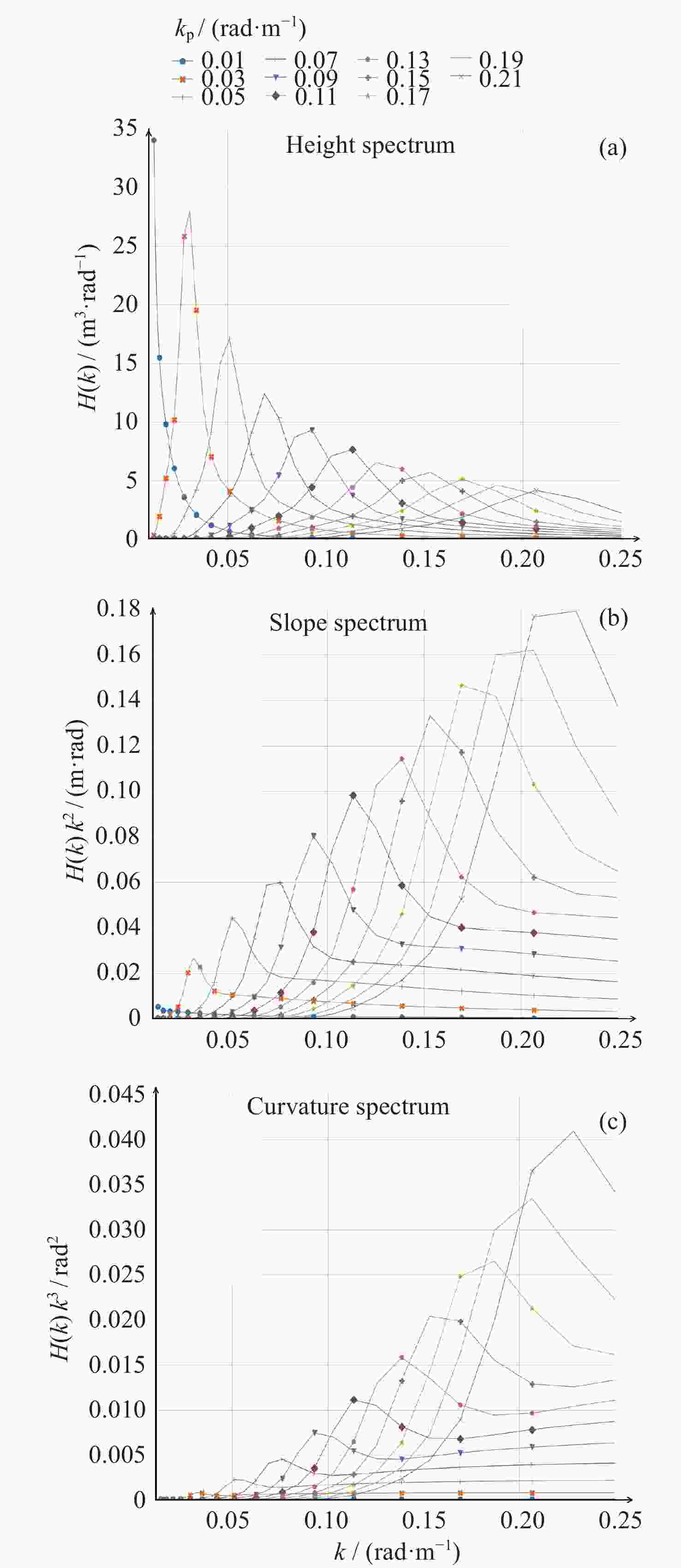
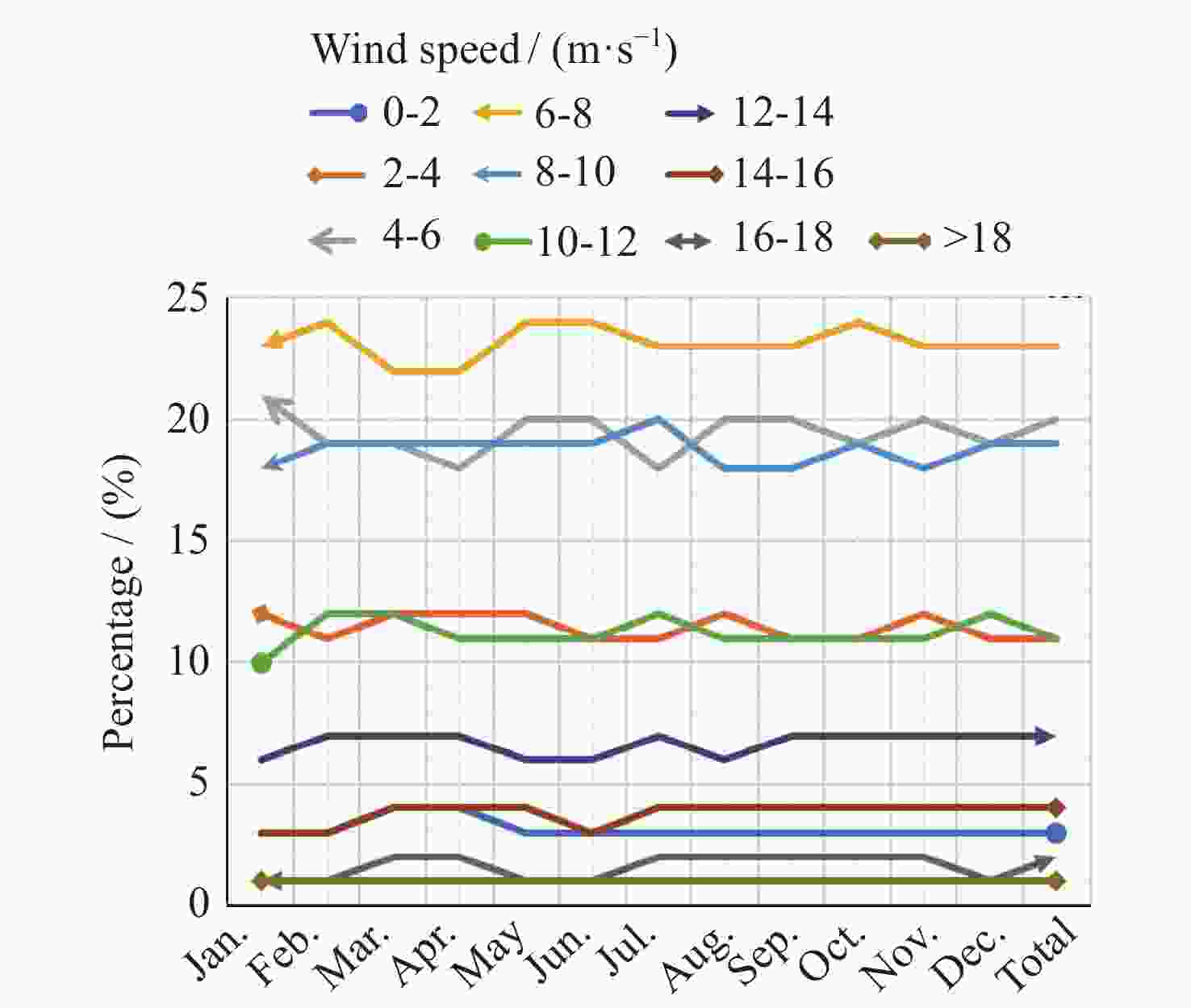
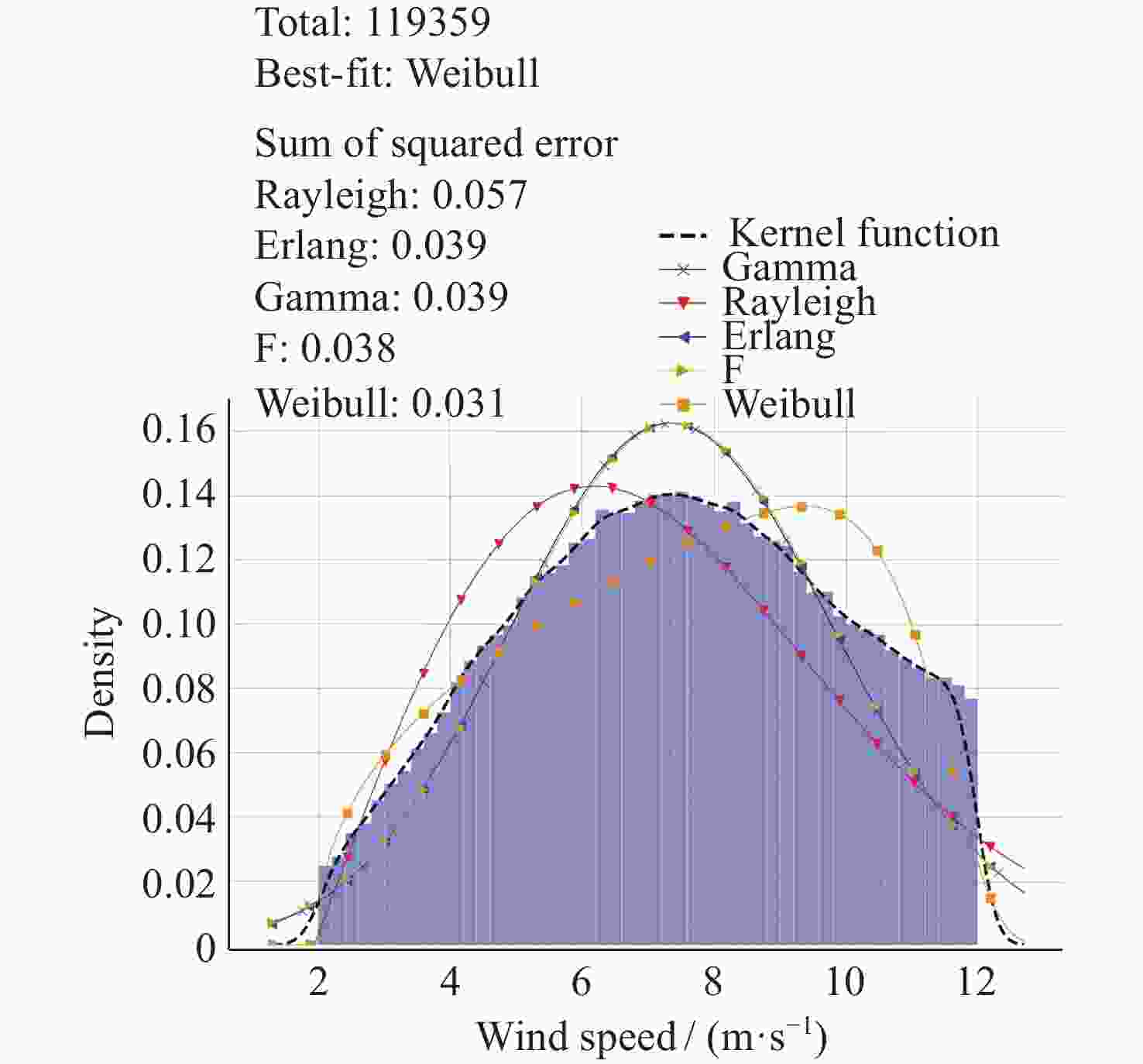
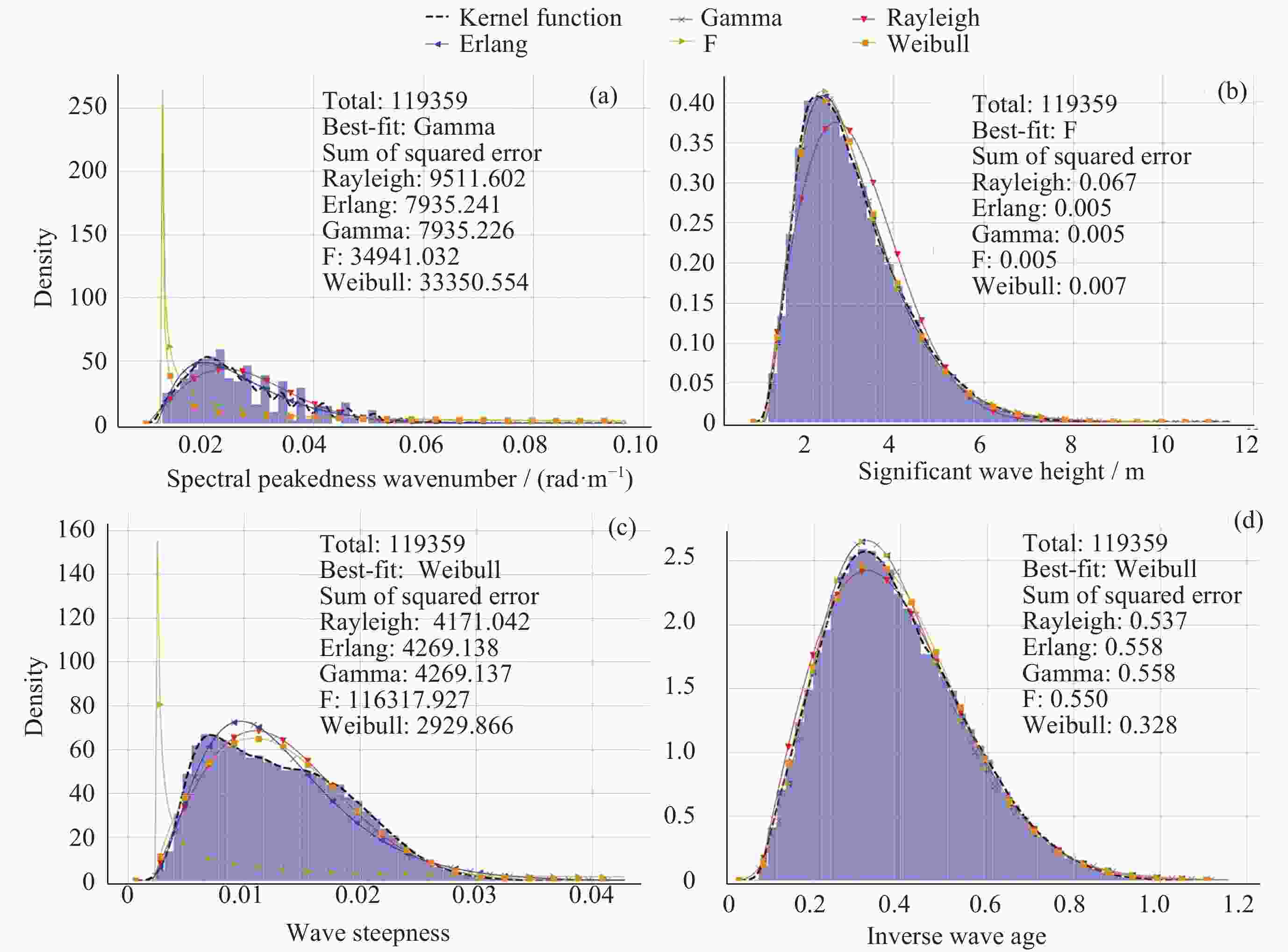
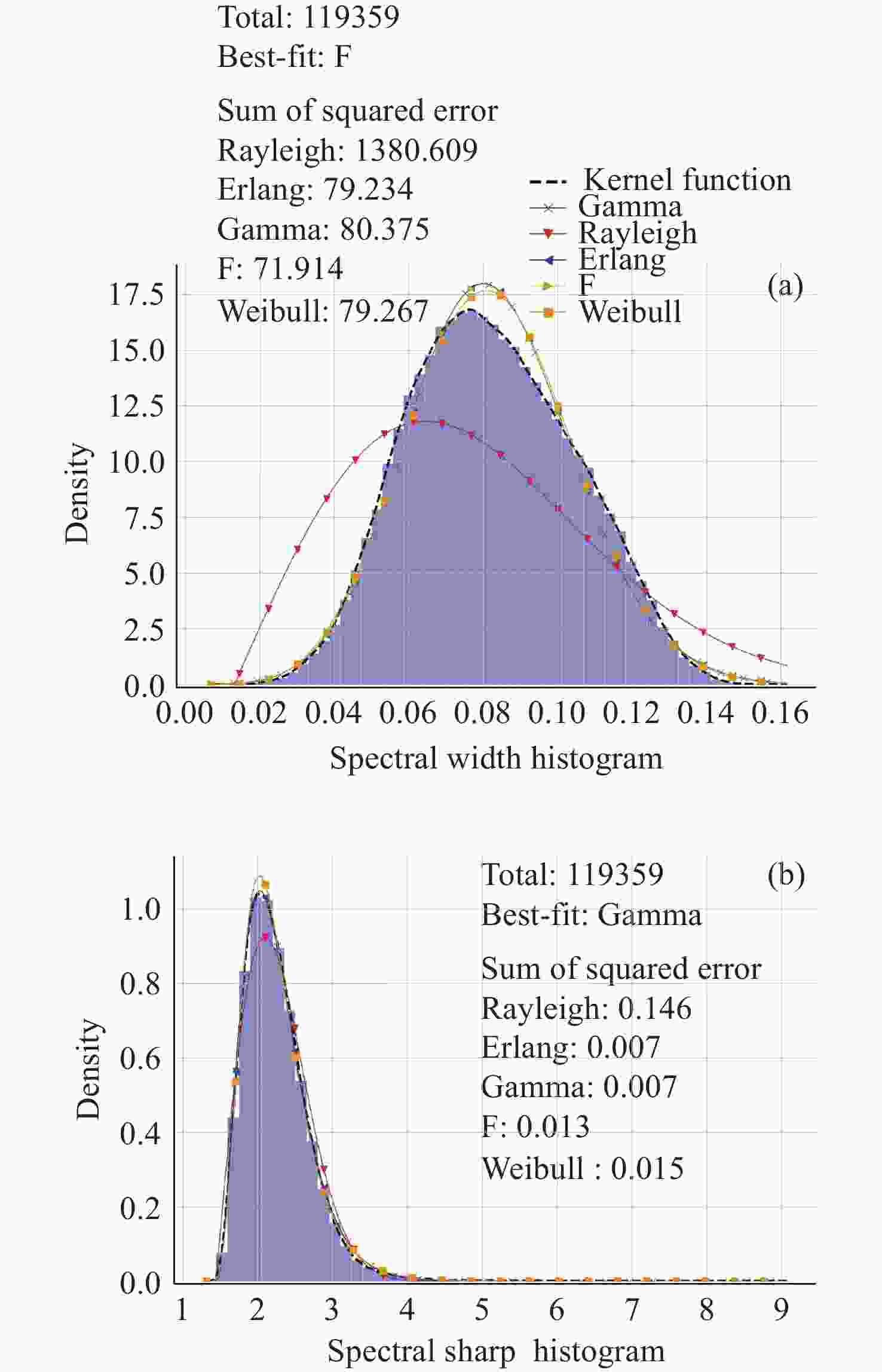
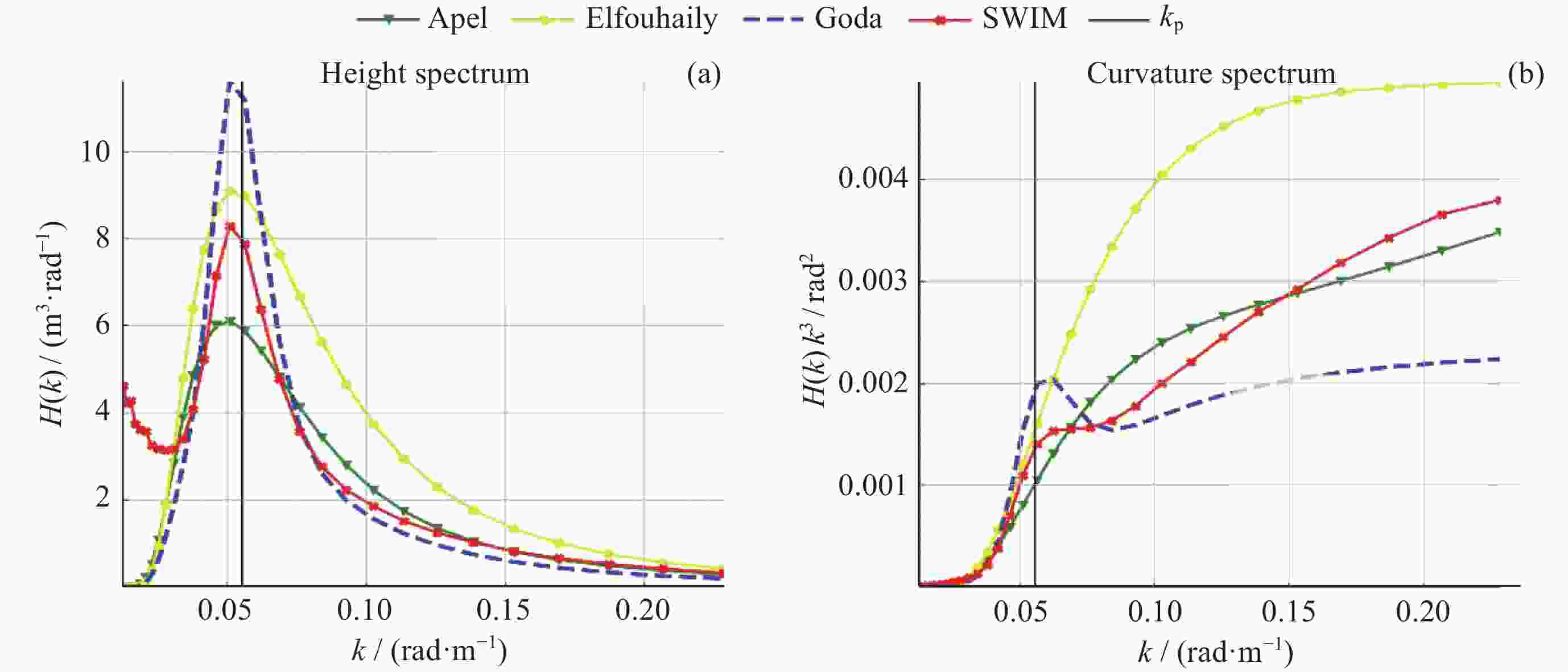
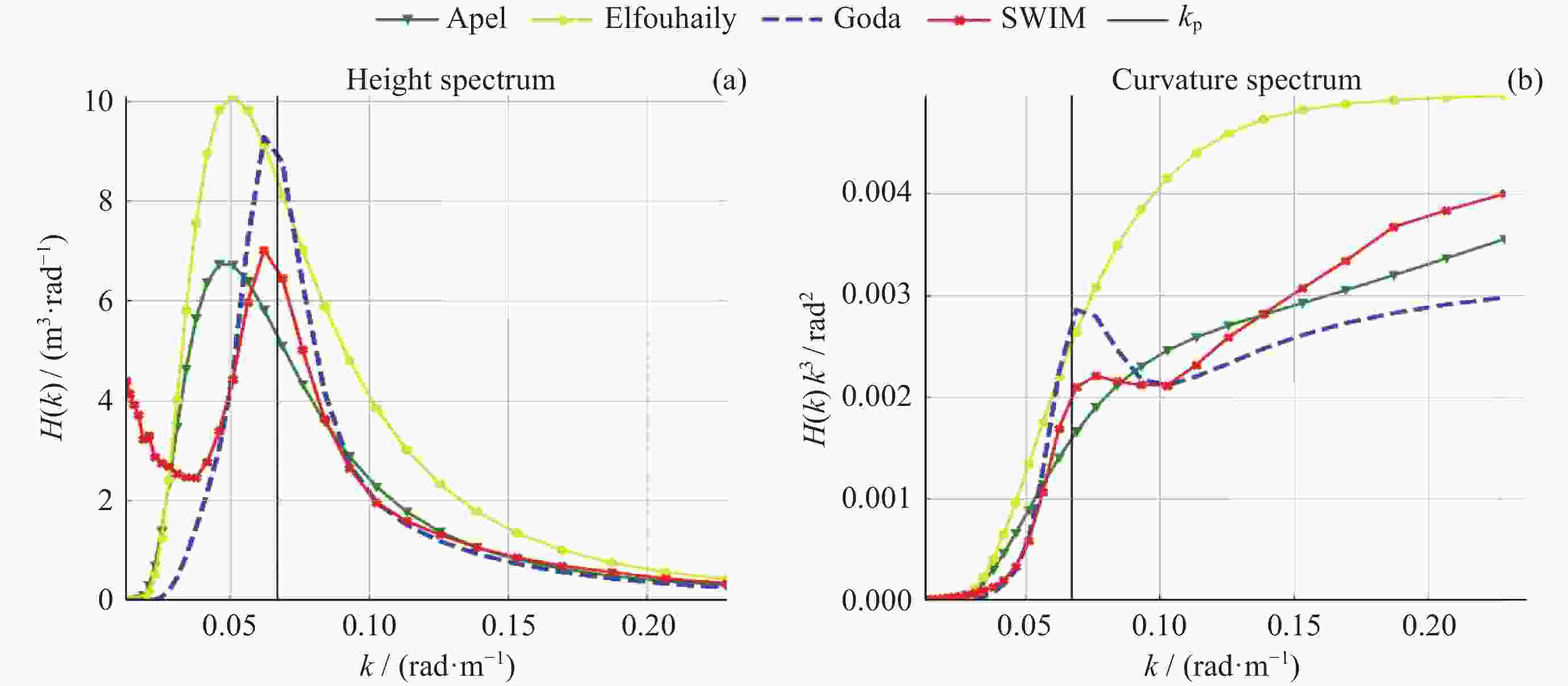
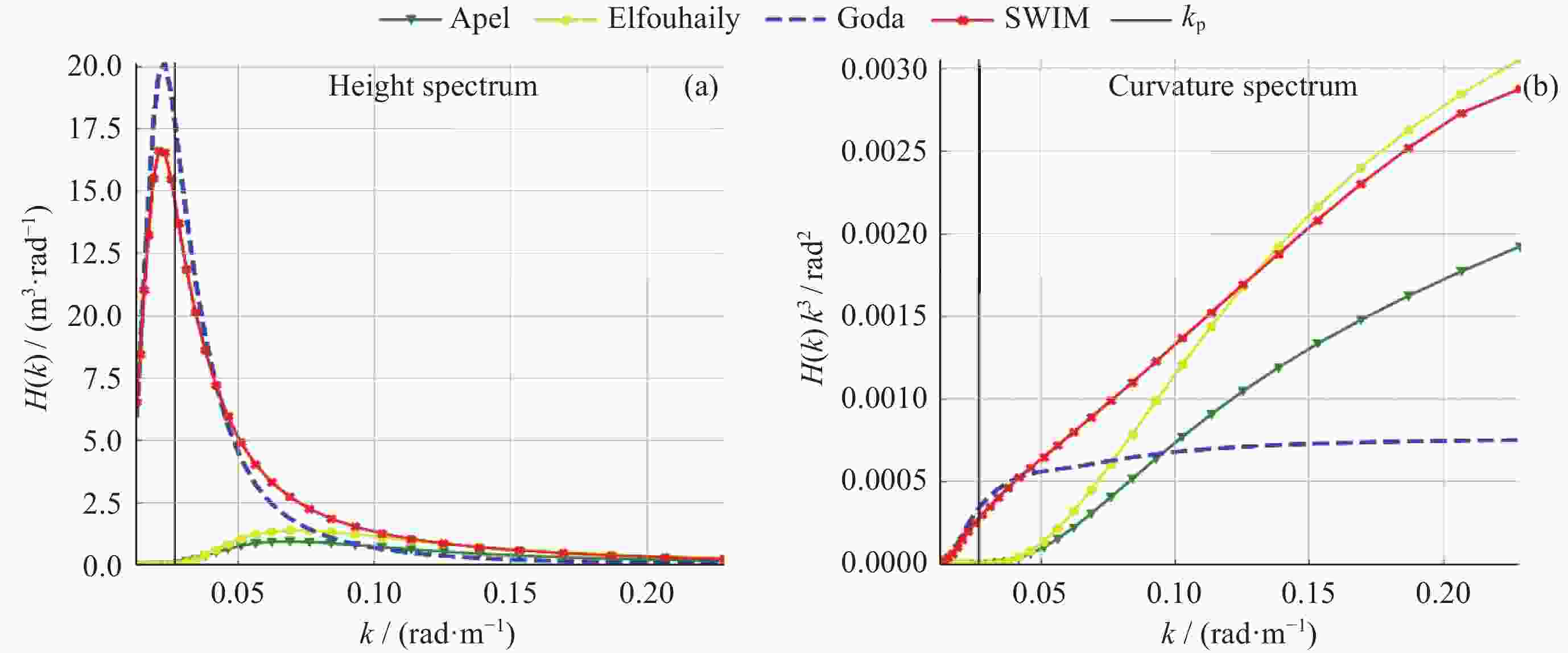
摘要: 海浪谱模型不仅能表征粗糙海表面，还能揭示海浪能量随波数和方向的分布，为海洋探测等研究和应用提供必要信息。中法海洋卫星搭载的波谱仪可实现全球海浪方向谱的空间观测。根据现有海浪谱模型和海浪谱观测的发展现状，对波谱仪观测的海浪参数进行统计特征分析，在波谱仪观测的波数范围内（0.01～0.25 rad·m–1），进行不同海态下实测海浪谱与以Apel谱、Elfouhaily谱和Goda谱为代表的波高谱和曲率谱模型的比较，得到现有海浪谱观测与上述三种谱模型的差异，并结合海浪参数统计特征，对产生差异的原因进行讨论分析。结果表明，现有谱与波谱仪观测的差异来自于其对海态的不完全表达，且所表示的海态在自然状态中仅占有限比例。研究结论可以为海浪谱模型和观测的后续研究提供支持。Abstract: The ocean wave spectrum models not only characterize the rough sea surface but also reveal the internal energy distribution of waves with wave numbers and directions, providing information for air-sea interaction research and ocean exploration applications. The Surface Waves Investigation and Monitoring instrument (SWIM) onboard the China France Oceanography Satellite (CFOSAT) can obtain spatial observations of global ocean wave directional spectra. In this research, the status of existing wave spectrum models and observations were summarized, then the statistical characteristics of wave parameters observed by SWIM are analyzed. To investigate the specific performance of the Apel spectrum, Elfouhaily spectrum, and Goda spectrum model in different sea states, the sea states are labelled in different categories according to the well-applied wave field characterization features. Then the measured ocean wave spectra within the range of wave numbers (0.01～0.25 rad·m–1) under different sea states were compared with the height and curvature spectra in the spectrum models under different sea states. The differences between the existing wave observations and the above three spectra are quantified and combined in their statistical characteristics in terms of the ocean wave parameters. The results indicate that when the inverse wave age is less than 0.8, the Goda wave height spectrum and Elfouhaily curvature spectrum are the closest in terms of the wave height spectrum and curvature spectrum to SWIM observations respectively. When the inverse wave age is between 0.8 and 0.9, the Apel wave height spectrum and curvature spectrum are most closely aligned with the measured data from SWIM. When the inverse wave age is between 0.9 and 1.0, the Goda wave height spectrum and Apel curvature spectrum are most closely matched with the wave height spectrum and curvature spectrum from the SWIM product respectively. Conclusions are drawn that the reasons for the differences between SWIM observations and existing models mentioned above are due to their conditional assumptions and incomplete expression of the sea states, while in the natural sea environment, these assumptions hold but for quite a limited fraction. The result supports the follow-up research of wave spectrum model and observation applications.
-
图 4 $ {k}_{\rm{p}} $为0.048 rad·m–1时不同有效波高下的Goda谱
Figure 4. Goda spectrum at different significant wave height when $ {k}_{\rm{p}} $ is 0.048 rad·m–1
图 5 有效波高为3 m时不同$ {k}_{\rm{p}} $下的Goda谱
Figure 5. Goda spectrum at different $ {k}_{\rm{p}} $ when significant wave height is 3 m
图 10 逆波龄为0.8～0.9时SWIM数据与Apel谱、Elfouhaily谱、Goda谱的比较
Figure 10. Comparison between SWIM observations and spectrum models, such as Apel, Elfouhaily, Goda spectrum when inverse wave age rank is from 0.8 to 0.9
图 11 逆波龄为0.9～1.1时SWIM数据与Apel谱、Elfouhaily谱、Goda谱的比较
Figure 11. Comparison between SWIM observations and spectrum models, such as Apel, Elfouhaily, Goda spectrum when inverse wave age rank is 0.9～1.1
图 12 逆波龄<0.8时，SWIM数据与Apel谱、Elfouhaily谱、Goda谱的比较
Figure 12. Comparison between SWIM observations and spectrum models, such as Apel, Elfouhaily, Goda spectrum when inverse wave age rank is less than 0.8
表 1 不同海态的海浪参数平均值
Table 1. Average value of wave parameters at different sea state
Significant wave
height/（m）Wind speed
/（m·s–1）Peak wavenumber
/（rad·m–1）Inverse wave age Wave steepness Width Sharp 0.8～0.9 2.795 11.266 0.055 0.843 0.024 0.114 2.146 0.9～1.1 2.706 11.470 0.067 0.944 0.029 0.116 2.259 <0.8 3.107 7.279 0.027 0.376 0.013 0.081 2.269 Total 3.087 7.416 0.027 0.388 0.013 0.082 2.259 
下载: 导出CSV
表 2 逆波龄为0.8～0.9，SWIM与Apel谱、Elfouhaily谱和Goda谱的一致性评价指标
Table 2. Consistency evaluation indicators for SWIM with Apel spectrum, Elfouhaily spectrum, and Goda spectrum, when inverse wave age rank is from 0.8 to 0.9
Apel波高谱/曲率谱 Elfouhaily波高谱/曲率谱 Goda波高谱/曲率谱 RMSE 2.015/0.000 2.400/0.001 2.235/0.001 R-Square 0.096/0.971 –0.284/0.200 –0.113/0.785 DI 0.228/0.099 0.562/0.583 0.329/0.300
下载: 导出CSV
表 3 逆波龄为0.9～1.1时SWIM与Apel谱、Elfouhaily与Goda谱的一致性评价指标
Table 3. Consistency evaluation indicators for SWIM with Apel spectrum, Elfouhaily spectrum, and Goda spectrum, when inverse wave age rank is from 0.9 to 1.1
Apel波高谱/曲率谱 Elfouhaily波高谱/曲率谱 Goda波高谱/曲率谱 RMSE 2.163/0.000 3.102/0.001 2.093/0.000 R-Square –0.583/0.971 –2.254/0.416 –0.481/0.916 DI 0.313/0.106 0.740/0.516 0.304/0.181
下载: 导出CSV
表 4 逆波龄<0.8，SWIM与Apel谱、Elfouhaily谱和Goda谱的一致性评价指标
Table 4. Consistency evaluation indicators for SWIM with Apel spectrum, Elfouhaily spectrum, and Goda spectrum, when inverse wave age rank is less than 0.8
Apel波高谱/曲率谱 Elfouhaily波高谱/曲率谱 Goda波高谱/曲率谱 RMSE 8.260/0.001 8.234/0.000 1.453/0.001 R-Square –1.178/0.591 –1.164/0.885 0.933/0.086 DI 0.837/0.416 0.759/0.125 0.232/0.603
下载: 导出CSV
-
[1] HAUSER D, TISON C, AMIOT T, et al. SWIM: the first spaceborne wave scatterometer[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(5): 3000-3014 doi: 10.1109/TGRS.2017.2658672 [2] 文圣常, 余宙文. 海浪理论与计算原理[M]. 北京: 科学出版社, 1984WEN Shengchang, YU Zhouwen. Theory and Computation Principle of Ocean Waves[M]. Beijing: Science Press, 1984 [3] [日]合田良实. 港工建筑物的防浪设计[M]. 刘大中, 孙巨才, 译. 北京: 海洋出版社, 1984GODA Y [Japan]. Design of Harbor Structures against Random Seas[M]. LIU Dazhong, SUN Jucai, trans. Beijing: Ocean Press, 1984 [4] 杨生强. 南海北部台风影响下海浪谱研究[D]. 青岛: 中国科学院大学, 2015YANG Shengqiang. Research on the Northern South China Sea Wave Spectrum Under the Influence of Typhoon[D]. Qingdao: University of Chinese Academy of Sciences, 2015 [5] APEL J R. An improved model of the ocean surface wave vector spectrum and its effects on radar backscatter[J]. Journal of Geophysical Research: Oceans, 1994, 99(C8): 16269-16291 doi: 10.1029/94JC00846 [6] COX C, MUNK W. Measurement of the roughness of the sea surface from photographs of the sun’s glitter[J]. Journal of the Optical Society of America, 1954, 44(11): 838-850 doi: 10.1364/JOSA.44.000838 [7] ELFOUHAILY T, CHAPRON B, KATSAROS K, et al. A unified directional spectrum for long and short wind-driven waves[J]. Journal of Geophysical Research: Oceans, 1997, 102(C7): 15781-15796 doi: 10.1029/97JC00467 [8] KUDRYAVTSEV V N, MAKIN V K, CHAPRON B. Coupled sea surface-atmosphere model: 2. Spectrum of short wind waves[J]. Journal of Geophysical Research: Oceans, 1999, 104(C4): 7625-7639 doi: 10.1029/1999JC900005 [9] RYABKOVA M, KARAEV V, GUO J, et al. A review of wave spectrum models as applied to the problem of radar probing of the sea surface[J]. Journal of Geophysical Research: Oceans, 2019, 124(10): 7104-7134 doi: 10.1029/2018JC014804 [10] GUÉRIN C A, CAPELLE V, HARTMANN J M. Revisiting the Cox and Munk wave-slope statistics using IASI observations of the sea surface[J]. Remote Sensing of Environment, 2023, 288: 113508 doi: 10.1016/j.rse.2023.113508 [11] 宋莎莎. 机载波谱仪海浪谱反演方法研究[D]. 青岛: 国家海洋局第一海洋研究所, 2011SONG Shasha. Research on Airborne Wave Spectrometer Wave Spectrum Inversion[D]. Qingdao: First Institute of Oceanography, MNR, 2011 [12] 林文明, 董晓龙. 星载雷达波谱仪反演海浪谱的精度研究[J]. 海洋学报, 2010, 32(5): 9-16LIN Wenming, DONG Xiaolong. The resolution of ocean wave spectra retrieved by space-borne real aperture radar spectrometer[J]. Acta Oceanologica Sinica, 2010, 32(5): 9-16 [13] HAUSER D, TOURAIN C, LACHIVER J M. CFOSAT: A new mission in orbit to observe simultaneously wind and waves at the ocean surface[J]. Space Research Today, 2019, 206: 15-21 [14] HAUSER D, TOURAIN C, HERMOZO L, et al. New observations from the SWIM radar on-board CFOSAT: instrument validation and ocean wave measurement assessment[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(1): 5-26 doi: 10.1109/TGRS.2020.2994372 [15] ALPERS W R, ROSS D B, RUFENACH C L. On the detectability of ocean surface waves by real and synthetic aperture radar[J]. Journal of Geophysical Research: Oceans, 1981, 86(C7): 6481-6498 doi: 10.1029/JC086iC07p06481 [16] XU Y, HAUSER D, LIU J Q, et al. Statistical comparison of ocean wave directional spectra derived from SWIM/CFOSAT satellite observations and from buoy observations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5117520 [17] WANG H, MOUCHE A, HUSSON R, et al. Quantifying uncertainties in the partitioned swell heights observed from CFOSAT SWIM and Sentinel-1 SAR via triple collocation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 4207716 [18] MERLE LE E, HAUSER D, PEUREUX C, et al. Directional and frequency spread of surface ocean waves from CFOSAT/SWIM measurements[C]//Proceedings of 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS. Brussels, Belgium: IEEE, 2021: 7390-7393 [19] DU Y L, YANG X F, CHEN K S, et al. An improved spectrum model for sea surface radar backscattering at L-Band[J]. Remote Sensing, 2017, 9(8): 776 doi: 10.3390/rs9080776 [20] LUCAS C, GUEDES SOARES C. On the modelling of swell spectra[J]. Ocean Engineering, 2015, 108: 749-759 doi: 10.1016/j.oceaneng.2015.08.017 [21] MIAO Y J, DONG X L, BOURASSA M A, et al. Effects of ocean wave directional spectra on Doppler retrievals of ocean surface current[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 4204812 [22] HWANG P A. Comment on “A study of the slope probability density function of the ocean waves from radar observations” by D. Hauser et al.[J]. Journal of Geophysical Research: Oceans, 2009, 114(C2): C02008 -
-
下载:
计量
- 文章访问数: 1076
- HTML全文浏览量: 192
- PDF下载量: 123
-
被引次数:
0(来源:Crossref)
0(来源:其他)
