激光光热效应对双层流体热毛细对流主动调控机理研究
doi: 10.11728/cjss2024.02.2023-0036 cstr: 32142.14.cjss2024.02.2023-0036
-
段文豪：男, 1999年9月出生于河南周口. 现为河海大学机电工程学院硕士研究生, 主要研究方向为微重力流体与传热、光热调控技术等E-mail: 211319010007@hhu.edu.cn
作者简介:
通讯作者:
Study on the Active Regulation Mechanism of Laser Photothermal Effect on Thermocapillary Convection of Double-layer Fluid
-
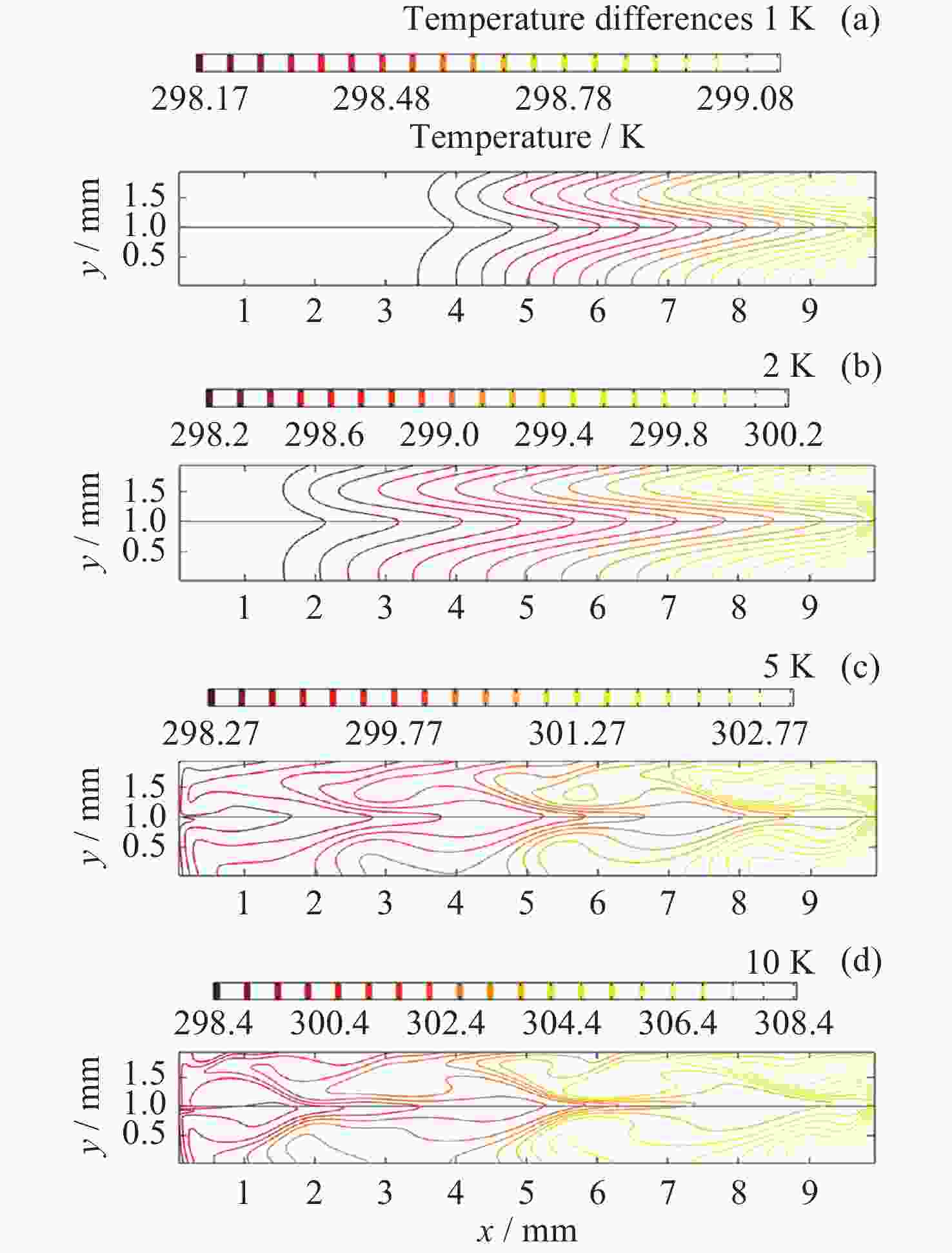
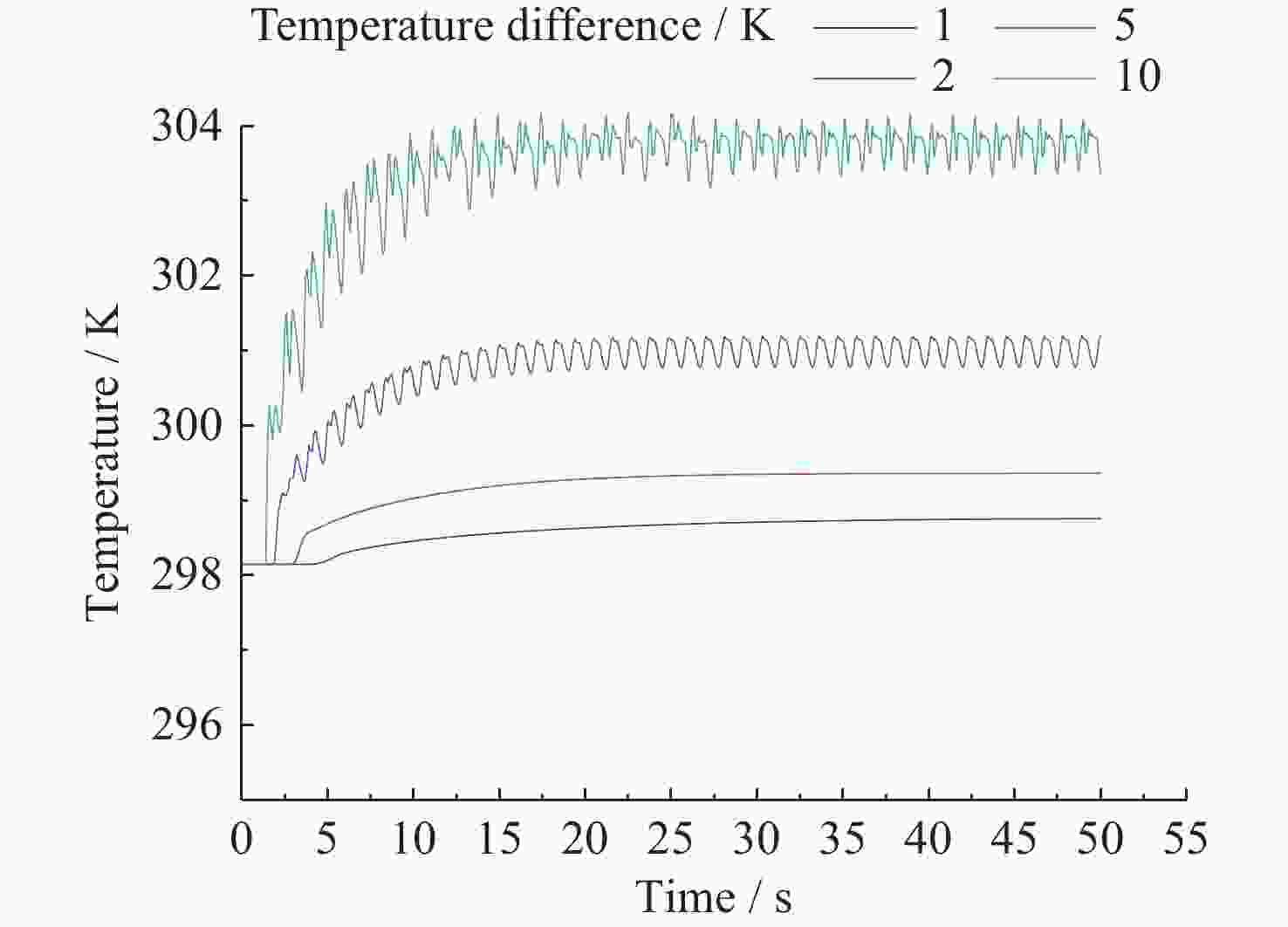
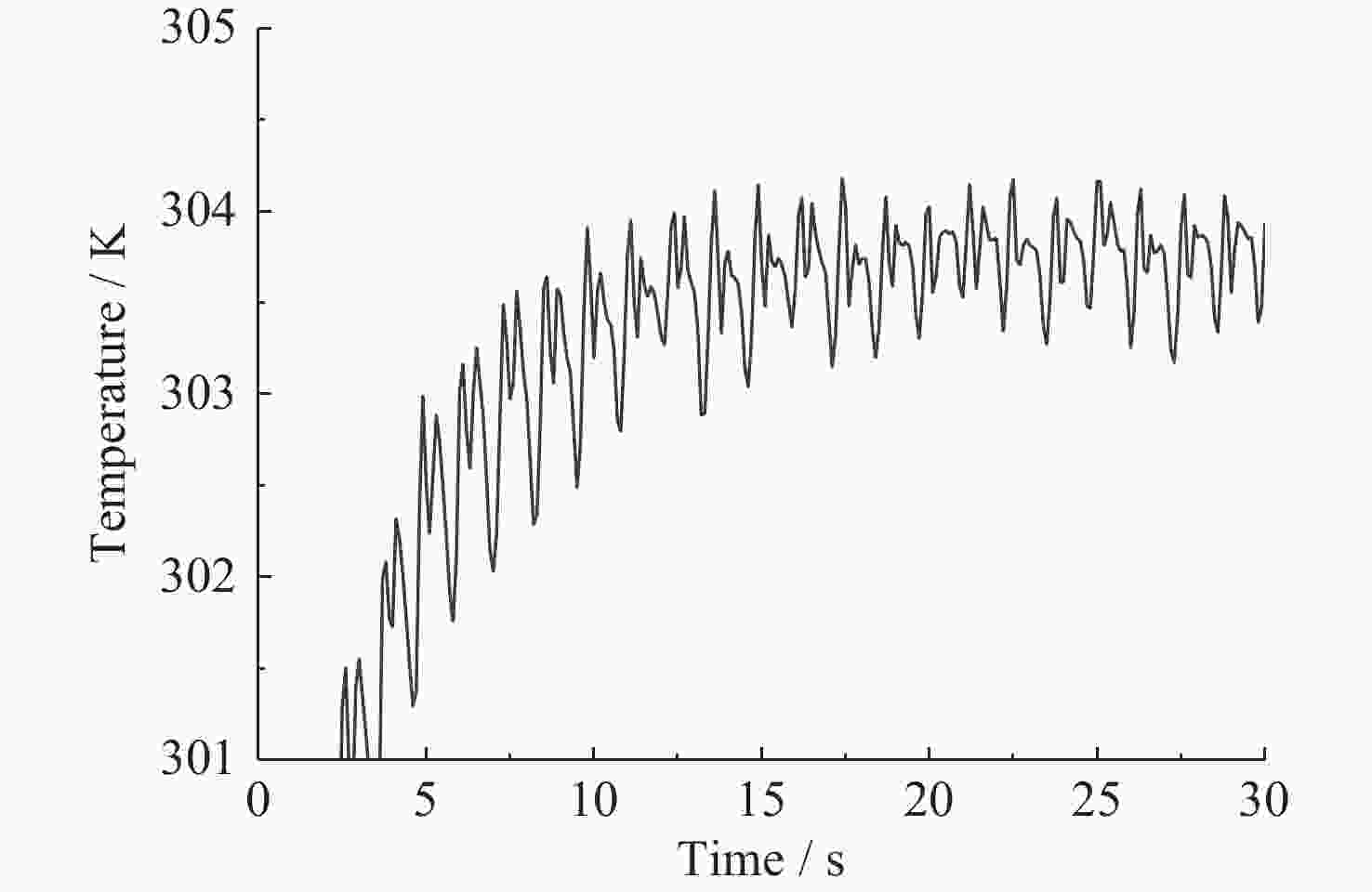
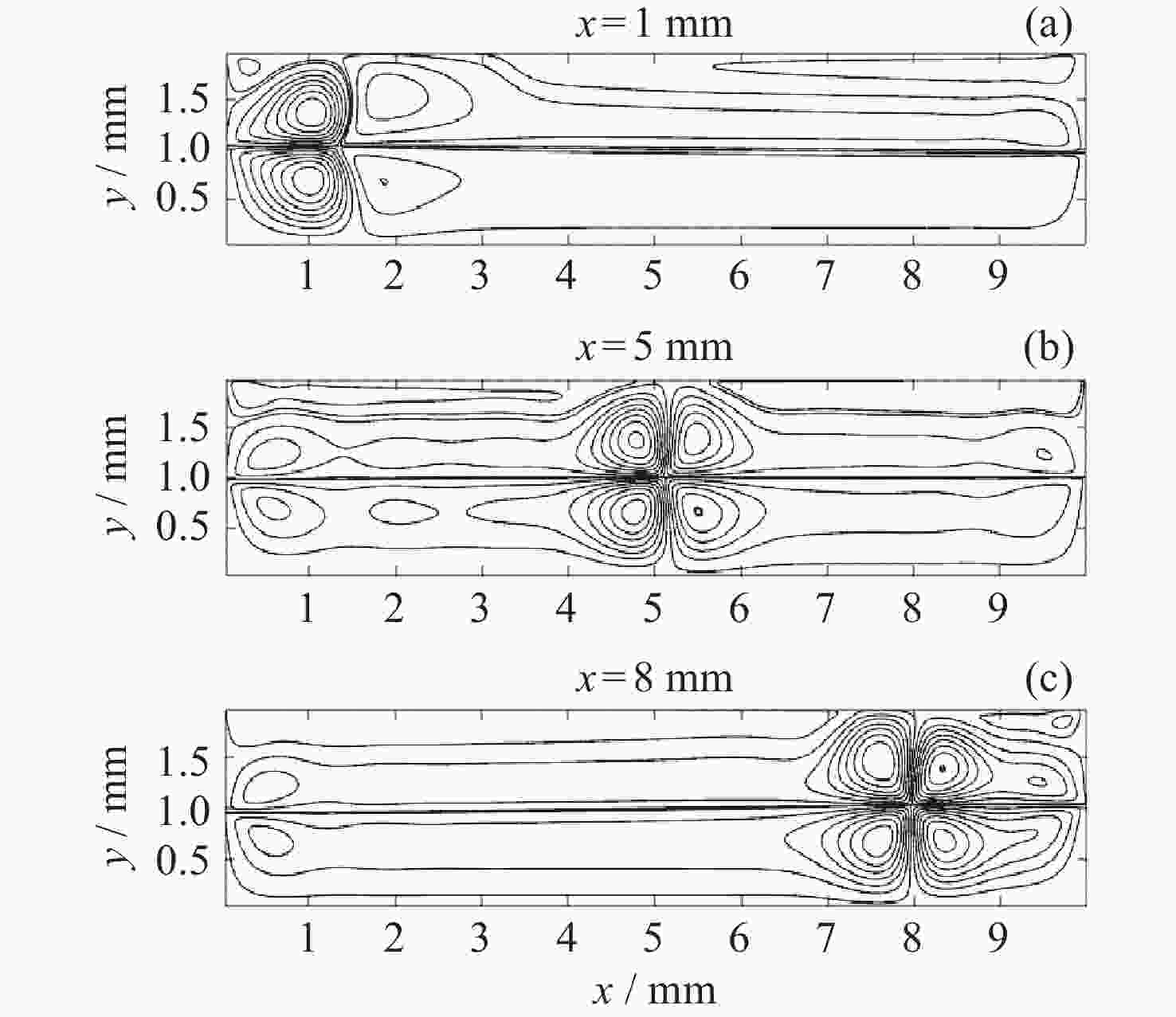
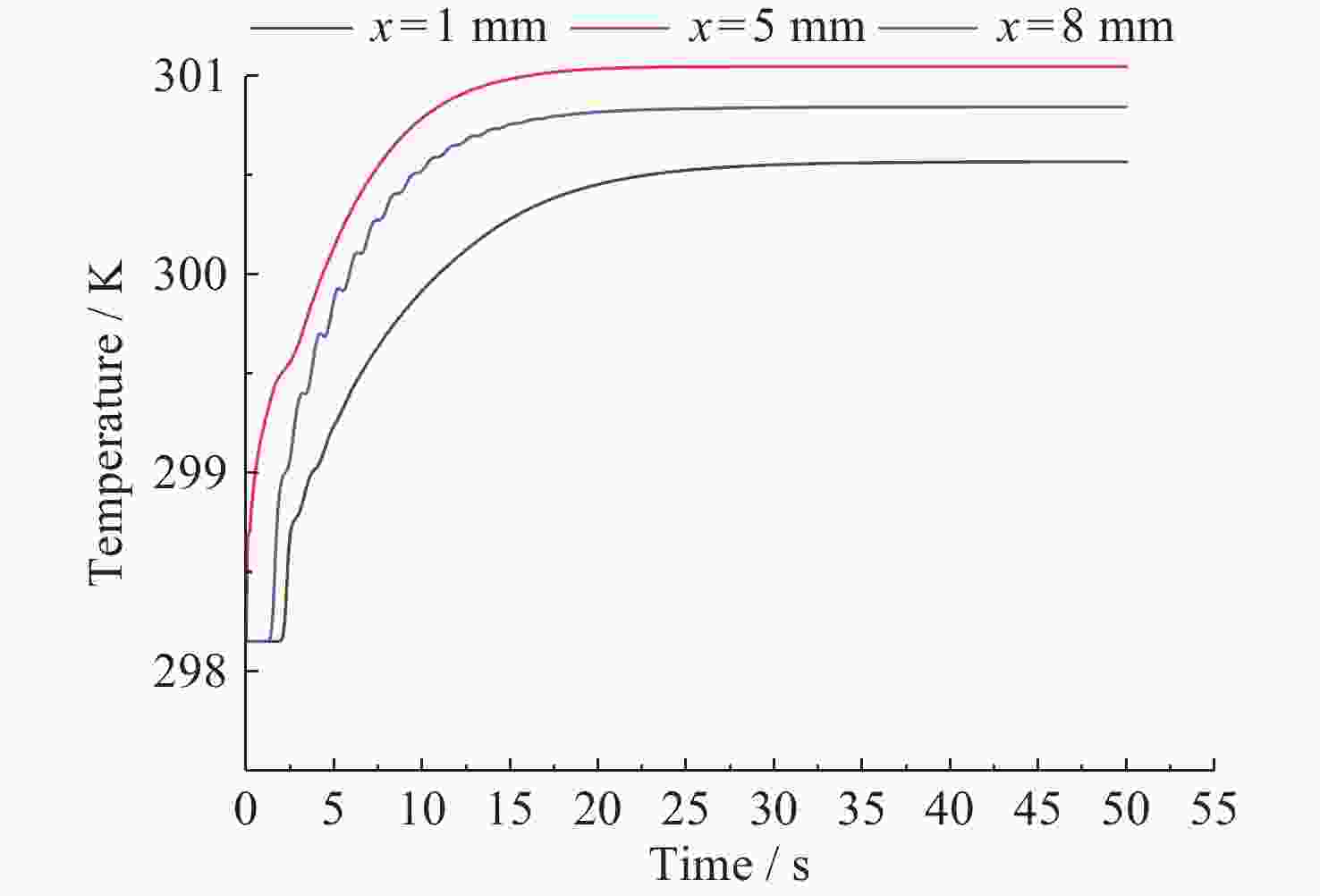
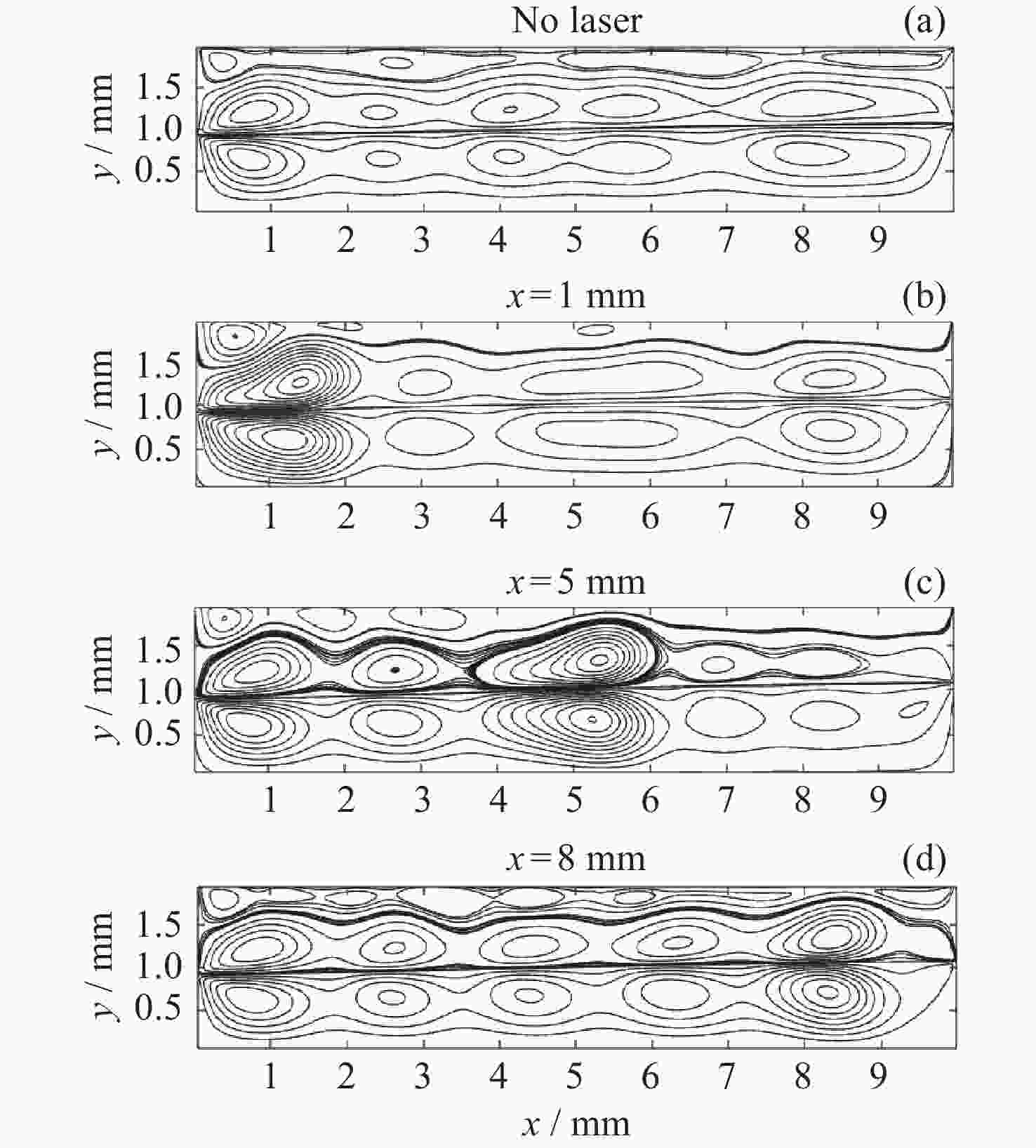
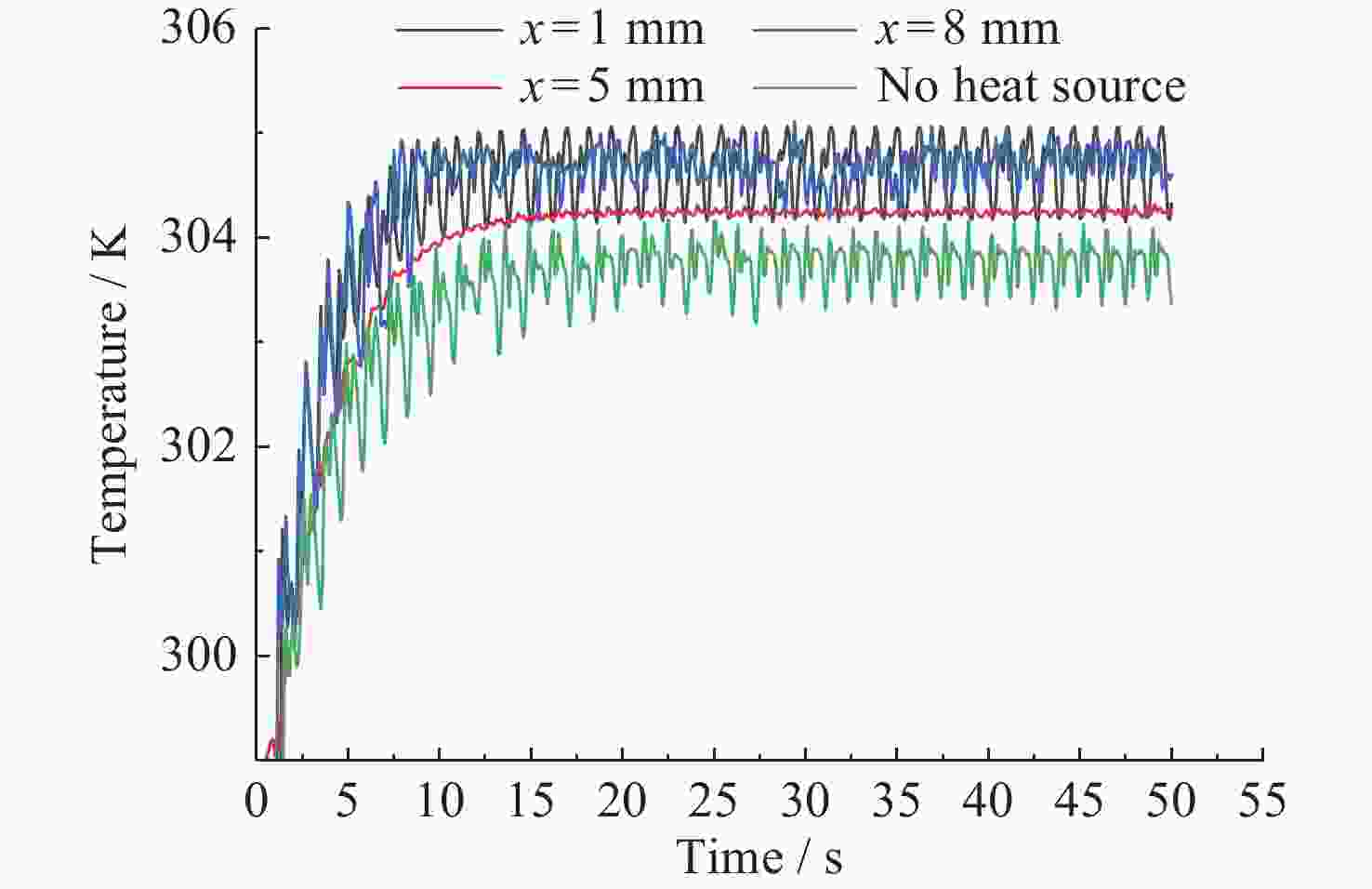
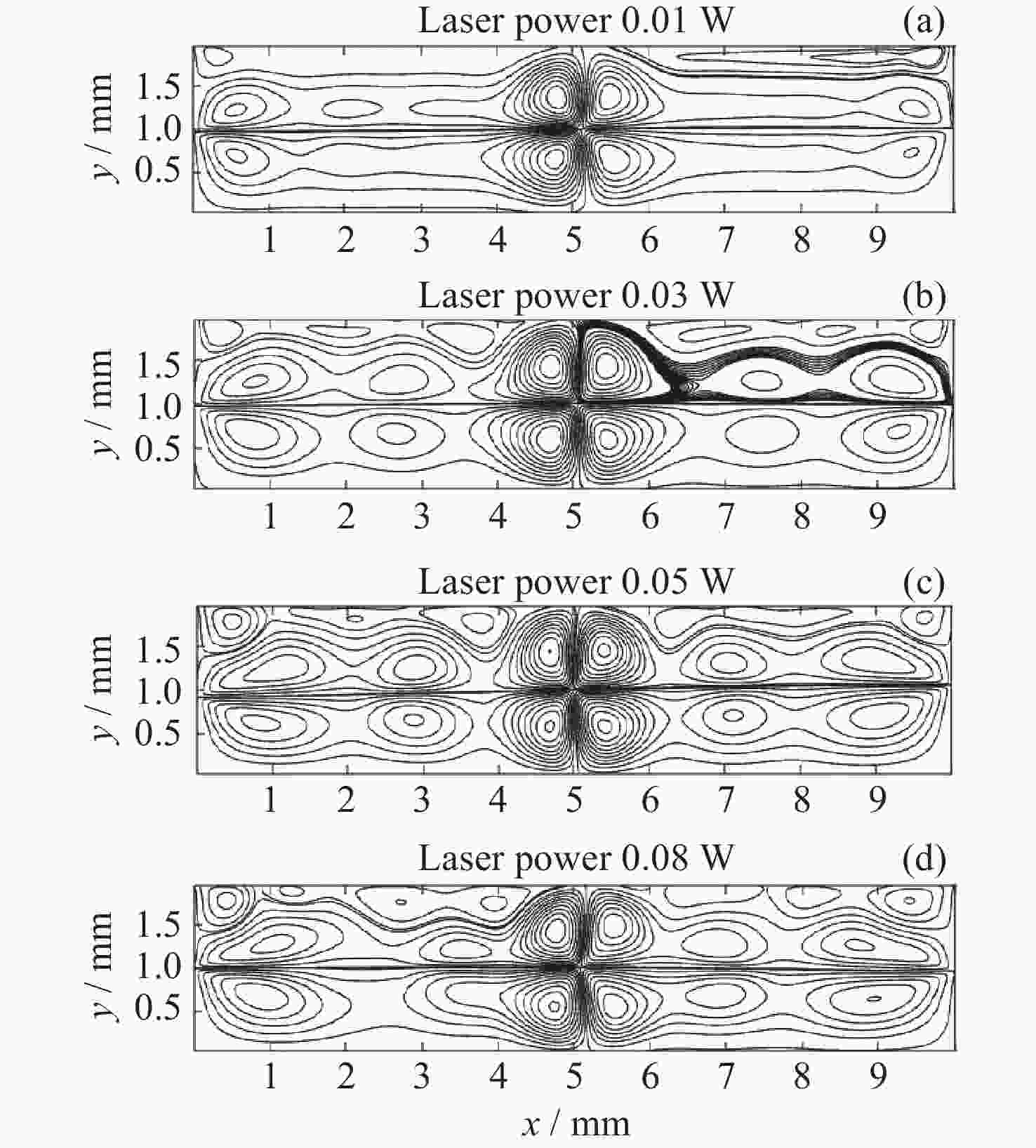
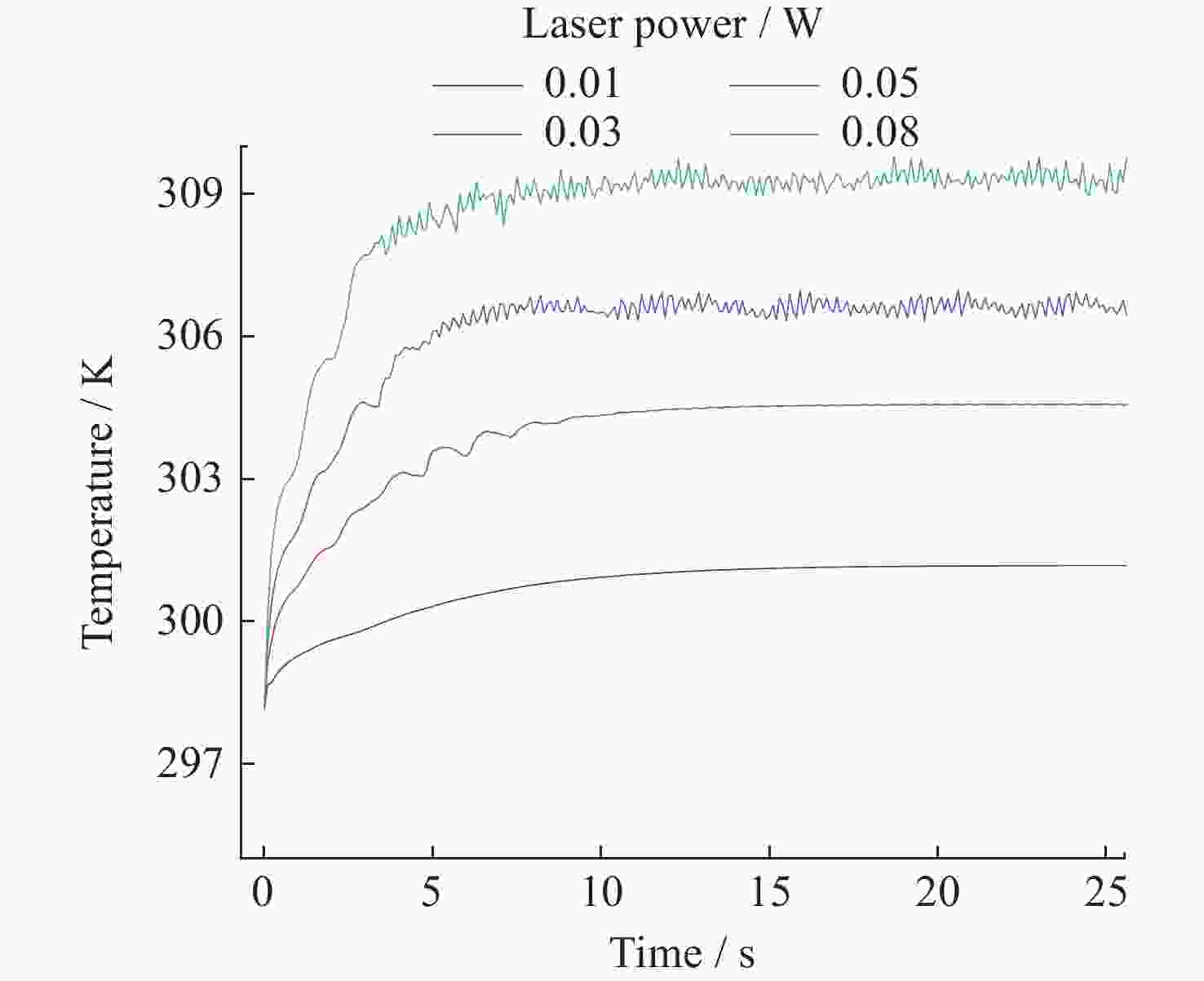
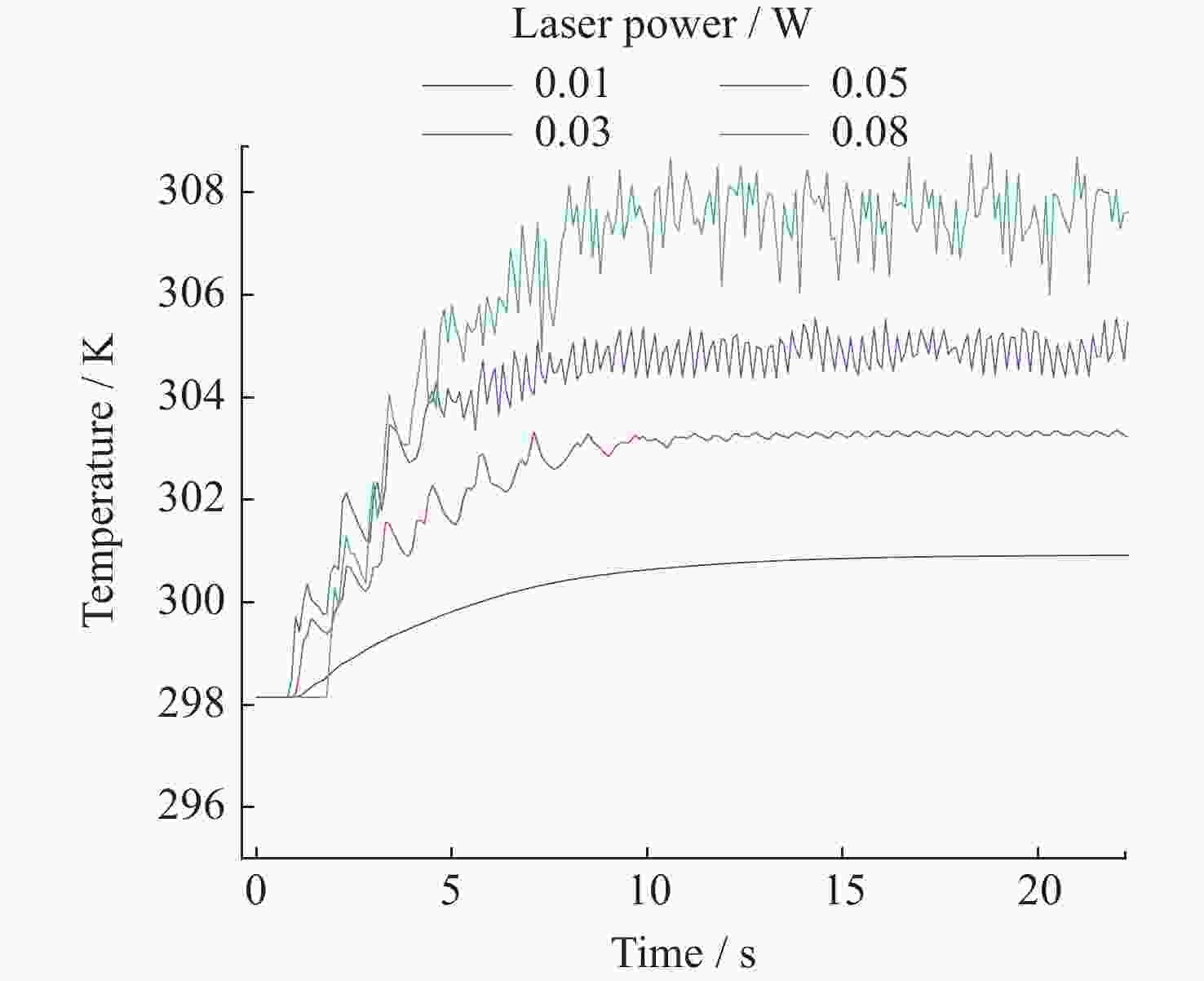
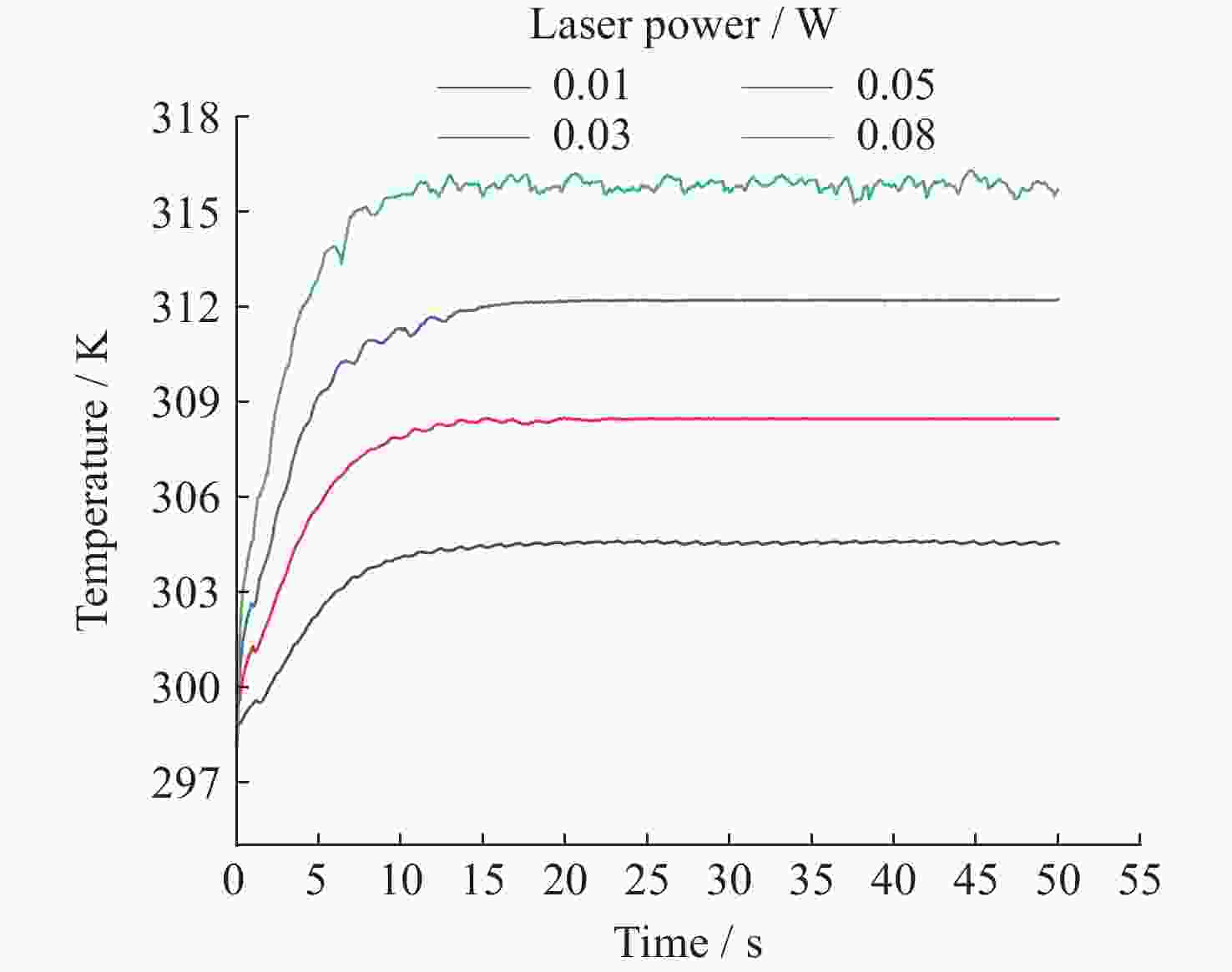
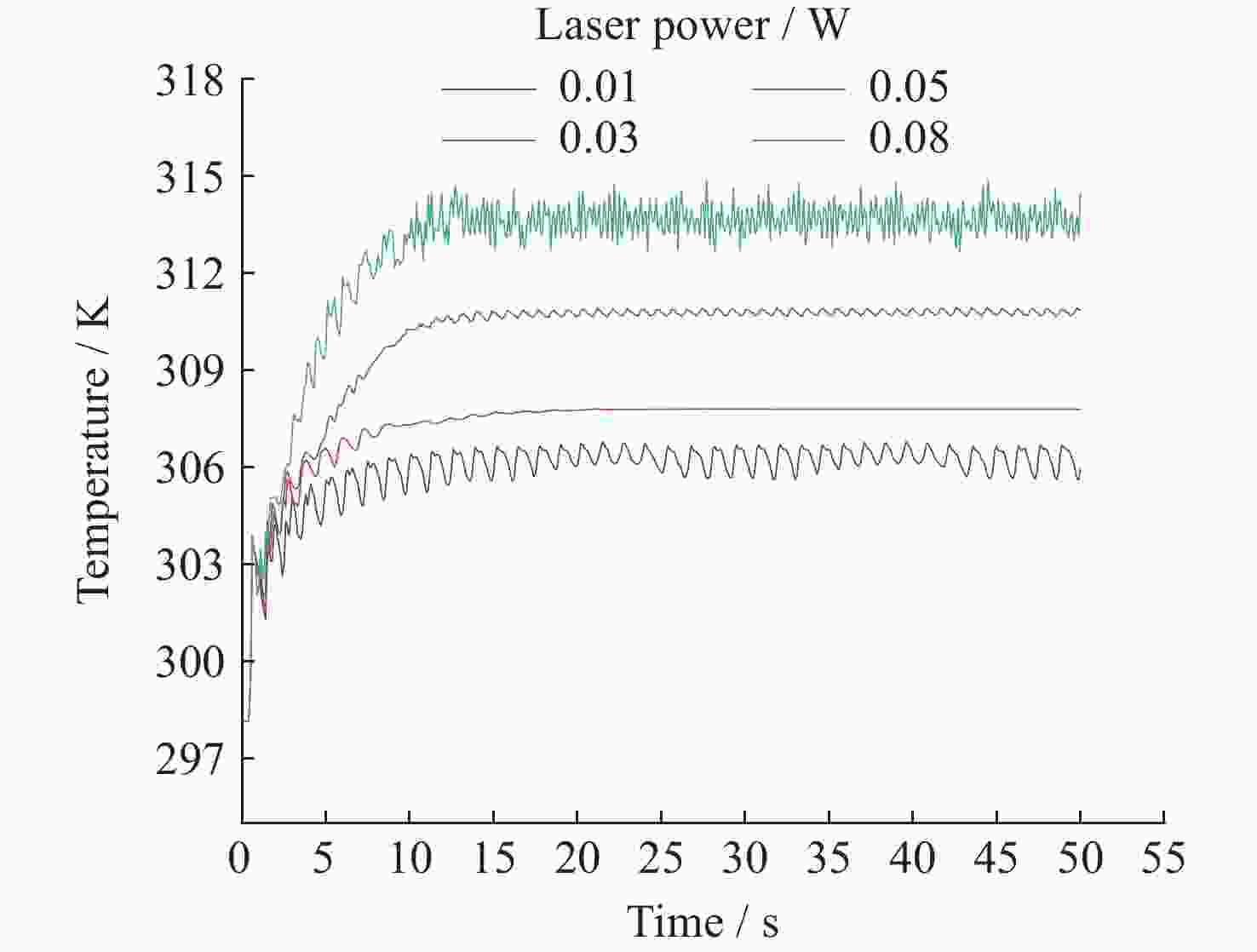
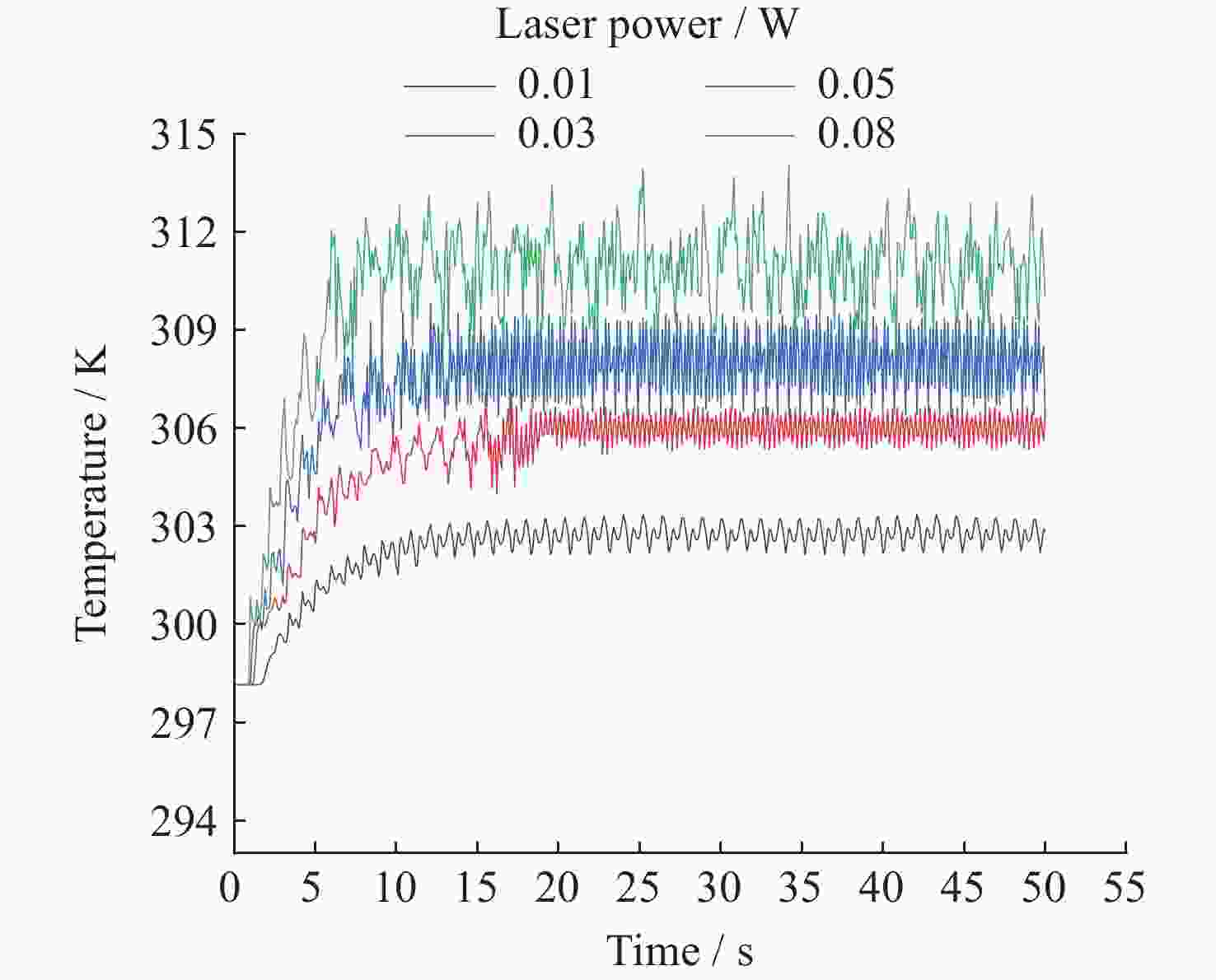
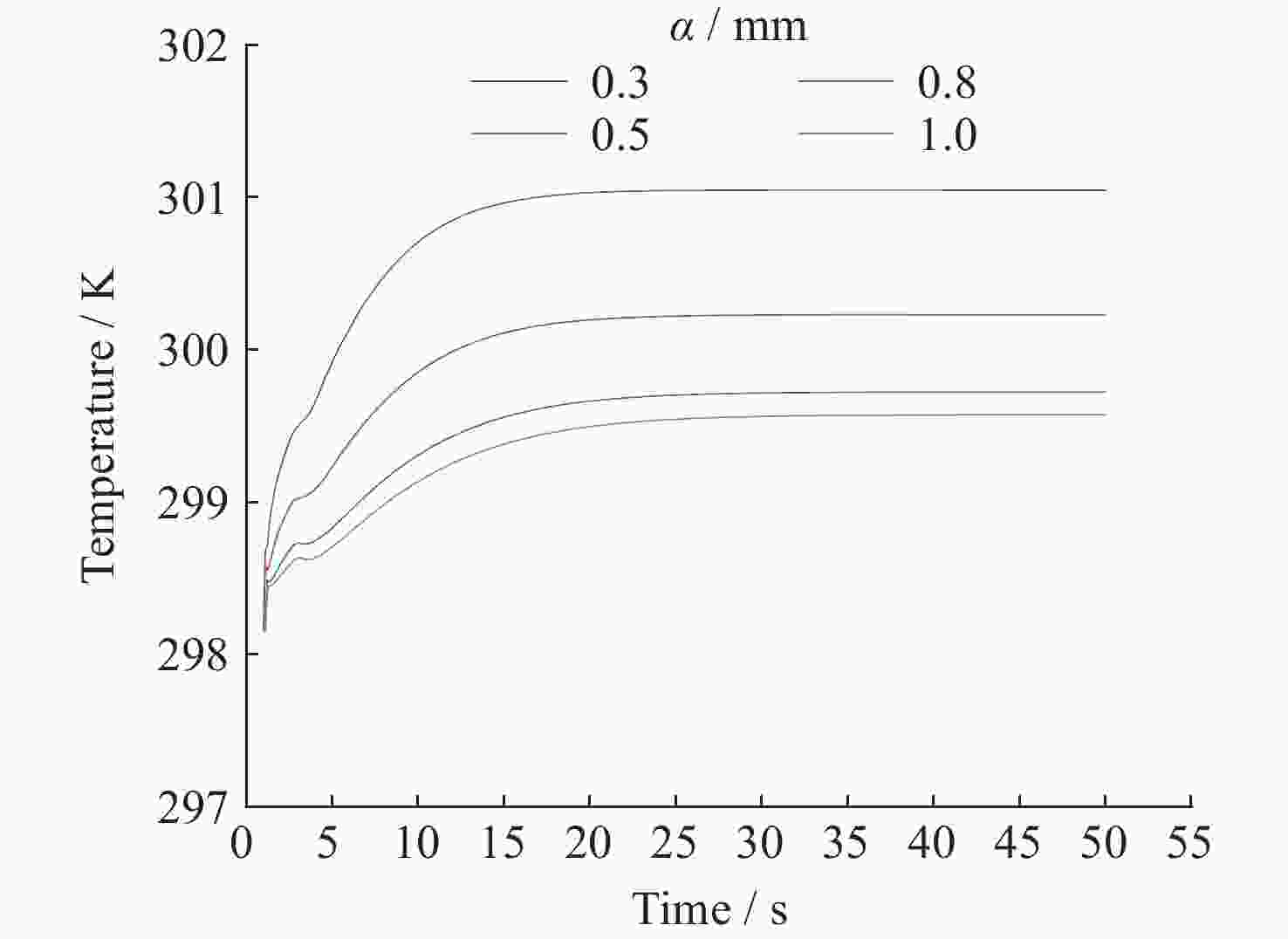
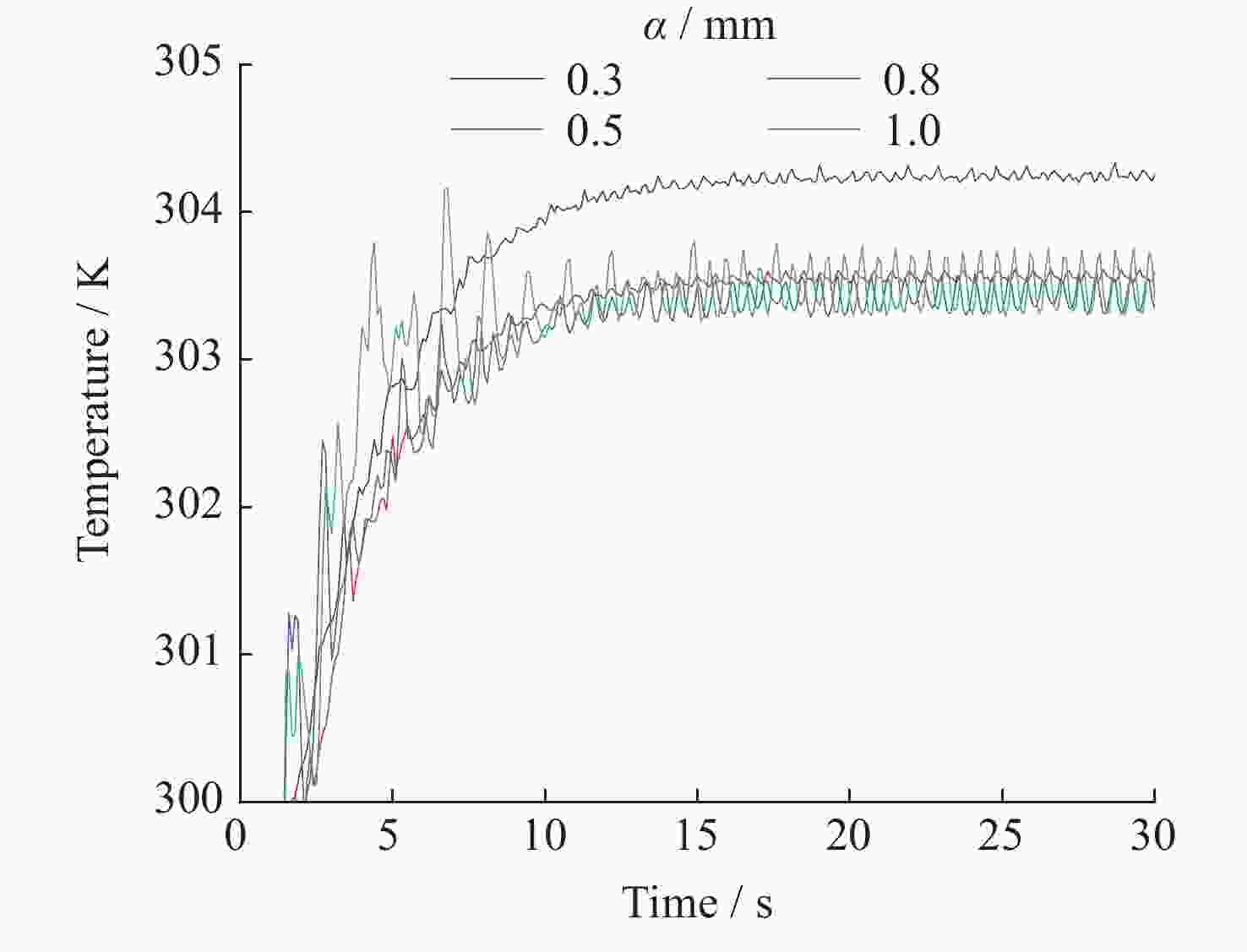
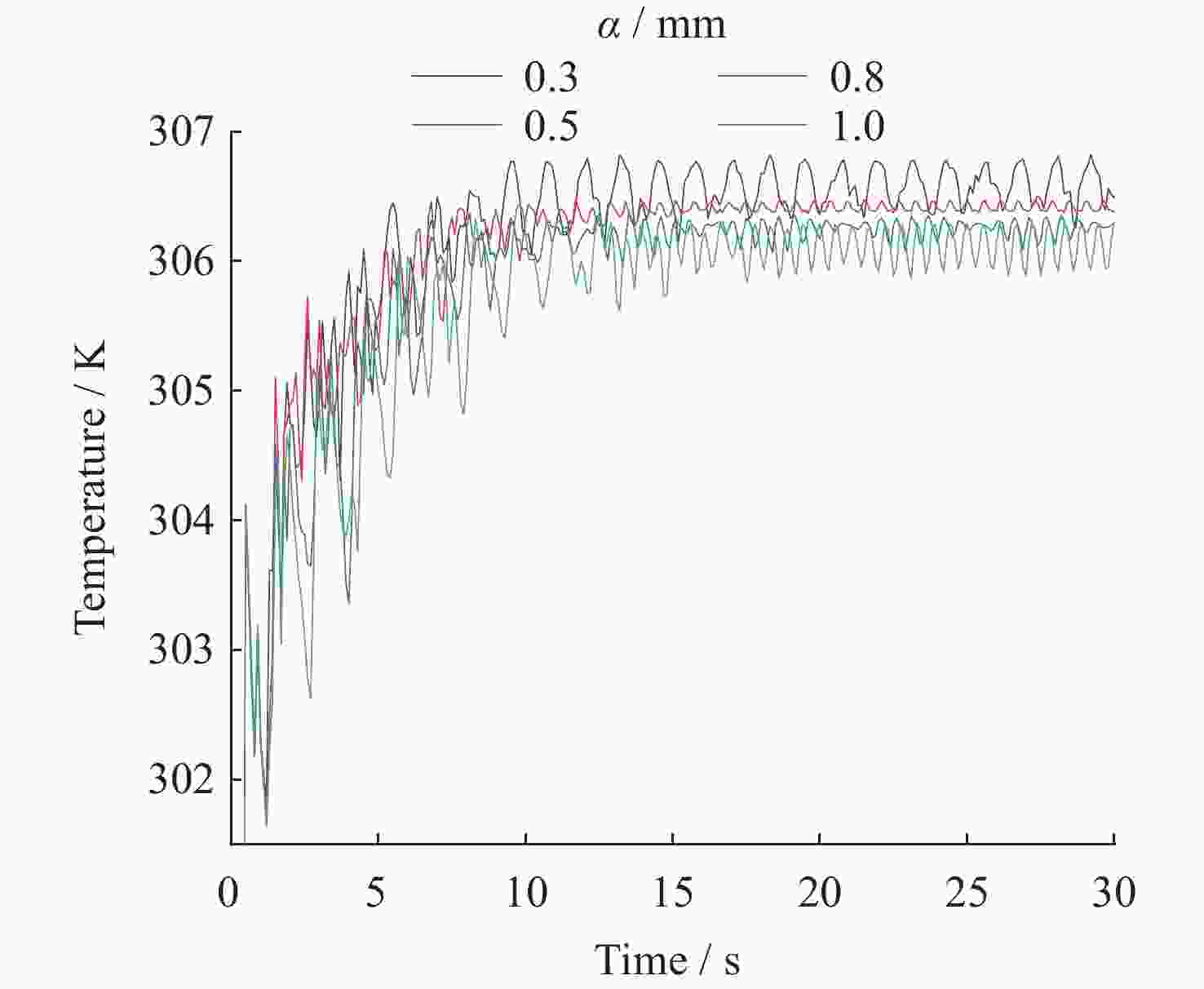
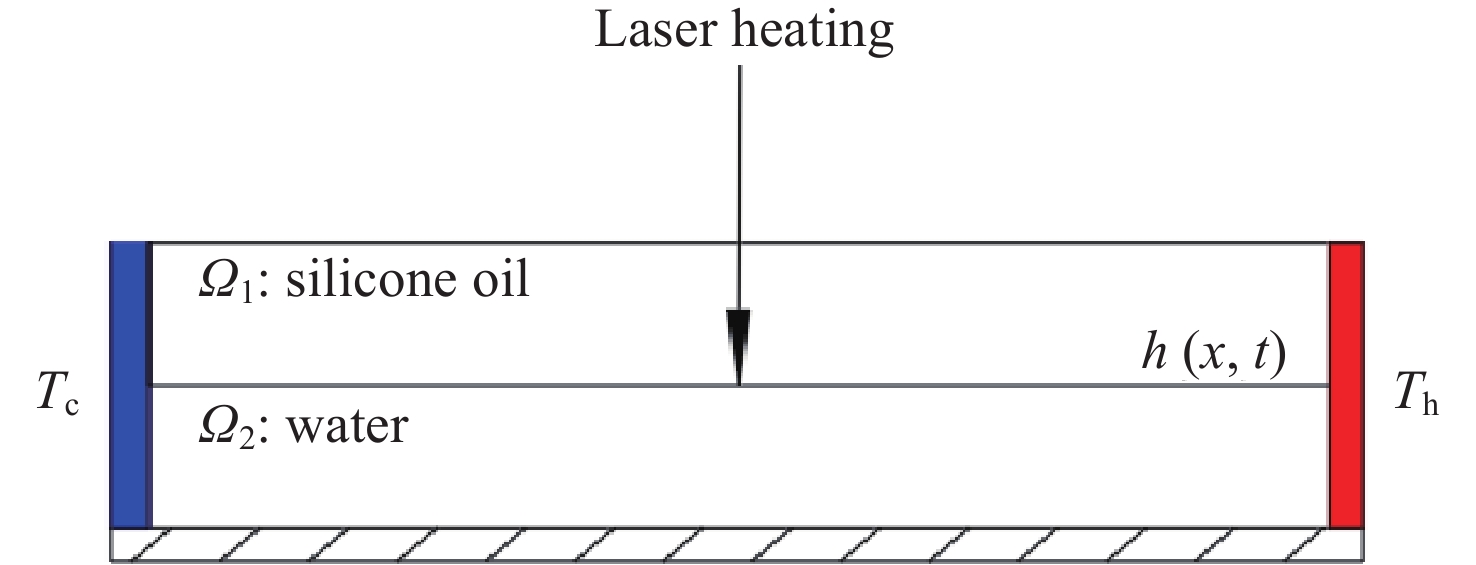
摘要: 热毛细对流不稳定性的主动调控是微重力流体力学和传热传质学领域的前沿问题, 为了实现双层流体热毛细对流不稳定性的有效控制, 提出利用激光光热效应对其不稳定性进行主动调控, 并模型化研究了激光光热效应参数(激光束位置、激光功率和光斑尺寸)对双层热毛细对流不稳定性的调控作用机理. 计算结果显示, 激光功率和光斑尺寸的调整能够显著改变双层流体热毛细对流的对流涡结构, 并减小温度波的振动幅度. 在一定工况下, 热源附近温度波动范围由0.7 K变为0.1 K, 变化显著; 随光斑尺寸增大, 温度振荡幅度先减小后增大. 激光位置的调整能够影响液层局部对流涡的位置, 进而改变激光位置两侧对流强度, 实现局部区域的振荡不稳定流动的控制, 通过光热效应参数的合理选择, 可以实现对双层流体热毛细对流的有效控制.Abstract: Active control of thermocapillary convective instability is a frontier scientific issue in the field of microgravity hydrodynamics and heat and mass transfer. In order to achieve effective control of thermocapillary convective instability of double-layer fluid, this paper innovatively proposes to use laser photothermal effect to actively control flow, the regulation mechanism of laser photothermal effect parameters (laser beam position, laser power and spot size) on the instability of double-layer thermocapillary convection are also studied. The calculation results show that the adjustment of laser power and spot size can significantly change the convective vortex structure in the spot area and weaken the vibration amplitude of temperature wave. Under certain working conditions, the temperature fluctuation range near the heat source changes significantly from 0.7 K to 0.1 K. The amplitude of temperature oscillation decreases first and then increases with the increase of spot size. The adjustment of the laser position can affect the position of the local convection vortex in the liquid layer, and then change the convection intensity on both sides of the laser position, so as to realize the control of the oscillating and unstable flow in the local region, the effective control of thermocapillary convection of double-layer fluid can be realized through the reasonable selection of photothermal effect parameters.
-
图 4 不同温差下流体的流线分布
Figure 4. Fluid flow line distribution under various temperature differences
图 5 不同温差下流体的温度等值线
Figure 5. Contour map of fluid temperature under various temperature differences
图 6 不同温差下监测点M的温度变化
Figure 6. Temperature variation of monitoring point M under different temperature differences
图 7 $ \Delta T=10\;\mathrm{K} $时监测点M的温度变化
Figure 7. Temperature change at monitoring point M when $\Delta T=10 \;{\mathrm{K}} $
图 8 小温差激光点在不同位置时流体的流线分布
Figure 8. Fluid flow line distribution at different positions of laser under small temperature difference
图 9 小温差激光在不同位置处监测点M的温度变化
Figure 9. Temperature changes at monitoring point M at different positions of laser with small temperature differences
图 10 大温差激光在不同位置处流体的流线分布
Figure 10. Fluid flow line distribution at different positions of laser with large temperature difference
图 11 大温差激光在不同位置处监测点M温度变化
Figure 11. Temperature changes of monitoring point M at different positions of laser with large temperature difference
图 12 小温差不同激光功率下流体的流线分布
Figure 12. Fluid flow line distribution under small temperature difference and different laser powers
图 13 小温差不同激光功率下监测点M的温度变化
Figure 13. Temperature change diagram of monitoring point M under small temperature difference and different laser powers
图 14 小温差不同激光功率下监测点N的温度变化
Figure 14. Temperature change diagram of monitoring point N under small temperature difference and different laser powers
图 15 大温差不同激光功率下流体的流线分布
Figure 15. Fluid flow line distribution under large temperature difference and different laser powers
图 16 大温差不同激光功率下监测点M的温度变化
Figure 16. Temperature change diagram of monitoring point M under large temperature difference and different laser powers
图 17 大温差不同激光功率下监测点N的温度变化
Figure 17. Temperature change diagram of monitoring point N under large temperature difference and different laser powers
图 18 大温差不同激光功率下监测点Q的温度变化
Figure 18. Temperature change diagram of monitoring point Q under large temperature difference and different laser powers
图 19 小温差$ \Delta T=1\;\mathrm{K} $时不同标准差流体的流线分布
Figure 19. Fluid flow line distribution with different standard deviations at $ \Delta T=1\;\mathrm{K} $
图 20 小温差$ \Delta T=1\;\mathrm{K} $时不同标准差下监测点M温度变化
Figure 20. Temperature changes at monitoring point M with different standard deviations at $ \Delta T=1\;\mathrm{K} $
图 21 大温差$ \Delta T=10\;\mathrm{K} $时不同标准差流体流线分布
Figure 21. Fluid flow line distribution with different standard deviations at $ \Delta T=10\;\mathrm{K} $
图 22 大温差$ \Delta T=10\;\mathrm{K} $时不同标准差下监测点M温度的变化
Figure 22. Temperature changes at monitoring point M with different standard deviations at $ \Delta T=10\;\mathrm{K} $
图 23 大温差$ \Delta T=10\;\mathrm{K} $ 时不同标准差下监测点N温度的变化
Figure 23. Temperature changes at monitoring point N with different standard deviations at $ \Delta T=10\;\mathrm{K} $
表 1 网格独立性测试
Table 1. Grid independence test
网格数 上层流速/(m·s–1) 下层流速/(m·s–1) 5232 1.22×10–3 1.88×10–3 6437 1.12×10–3 1.81×10–3 11958 1.05×10–3 1.73×10–3 14596 1.01×10–3 1.73×10–3 16210 9.8×10–4 1.705×10–3 20388 9.7×10–4 1.7×10–3 
下载: 导出CSV
-
[1] 刘佳. 双向温度梯度作用下浮力–热毛细对流的线性稳定性分析[D]. 重庆: 重庆大学, 2019LIU Jia. Linear Stability Analysis of Buoyancy-thermocapillary Convection Driven by Bidirectional Temperature Gradients[D]. Chongqing: Chongqing University, 2019 [2] JIANG Y N, CHI F X, CHEN Q S, et al. Effect of substrate microstructure on thermocapillary flow and heat transfer of nanofluid droplet on heated wall[J]. Microgravity Science and Technology, 2021, 33(3): 37 doi: 10.1007/s12217-021-09888-2 [3] JIANG Y N, ZHOU X M, WANG Y. Effect of nanoparticle shapes on nanofluid mixed forced and thermocapillary convection in mini channel[J]. International Communications in Heat and Mass Transfer, 2020, 118: 104884 doi: 10.1016/j.icheatmasstransfer.2020.104884 [4] JIANG Y N, ZHOU X M, WANG Y. Comprehensive heat transfer performance analysis of nanofluid mixed forced and thermocapillary convection around a gas bubble in minichannel[J]. International Communications in Heat and Mass Transfer, 2020, 110: 104386 doi: 10.1016/j.icheatmasstransfer.2019.104386 [5] ZHOU X M, JIANG Y Q, WANG Y, et al. Comprehensive heat transfer performance analysis of liquid metal based nanofluid laminar flow in circular tube[J]. International Journal of Mechanical Sciences, 2020, 175: 105530 doi: 10.1016/j.ijmecsci.2020.105530 [6] JIANG Y N, ZHOU X M, WANG Y. Effects of nanoparticle shapes on heat and mass transfer of nanofluid thermocapillary convection around a gas bubble[J]. Microgravity Science and Technology, 2020, 32(2): 167-177 doi: 10.1007/s12217-019-09757-z [7] ZHOU X M, JIANG Y N, HOU Y, et al. Thermocapillary convection instability in annular two-layer system under various gravity levels[J]. Microgravity Science and Technology, 2019, 31(5): 641-648 doi: 10.1007/s12217-019-09742-6 [8] HAMED M, FLORYAN J M. Marangoni convection. Part 1. a cavity with differentially heated sidewalls[J]. Journal of Fluid Mechanics, 2000, 405: 79-110 doi: 10.1017/S002211209900734X [9] SOMEYA S, MUNAKATA T, NISHIO M, et al. Flow observation in two immiscible liquid layers subject to a horizontal temperature gradient[J]. Journal of Crystal Growth, 2002, 235(1/2/3/4): 626-632 [10] FONTAINE J P, SANI R L. Thermocapillary effects in a multilayered fluid system[C]//Proceedings of the 30th Aerospace Sciences Meeting and Exhibit. Reno: AIAA, 1992 [11] AZUMA H, YOSHIHARA S, OHNISHI M, et al. Upper layer flow phenomena in two immiscible liquid layers subject to a horizontal temperature gradient[C]. Microgravity Fluid Mechanics, 1992, 205-212 [12] GÉORIS P, LEGROS J C. Pure thermocapillary convection in a multilayer system: first results from the IML-2 mission[C]//Proceedings of the IXth European Symposium on Gravity-Dependent Phenomena in Physical Sciences Held at Berlin. Berlin: Springer, 1996: 299-311 [13] 周炳红, 刘秋生, 胡良, 等. 两层流体热毛细对流空间实验研究[J]. 中国科学E辑, 2002, 32 (3): 316-322ZHOU Binghong, LIU Qiusheng, HU Liang, et al. Space experiments of thermocapillary convection in two-liquid layers[J]. Science in China Series E: Technological Science, 2002, 45 (5): 552-560 [14] 乔莉莉. 蒸发薄液层的热毛细对流实验[D]. 北京: 中国科学院力学研究所, 2019QIAO Lili. Thermocapillary Convection Experiment of the Thin Evaporating Liquid Layer[D]. Beijing: Institute of Mechanics, Chinese Academy of Sciences, 2019 [15] 朱志强, 纪岩, 刘秋生, 等. 蒸发效应与热毛细对流耦合现象的实验研究[J]. 空间科学学报, 2008, 28(1): 12-16 doi: 10.11728/cjss2008.01.012ZHU Zhiqiang, JI Yan, LIU Qiusheng, et al. Experimental study on the coupling of thermocapillary convection and evaporation effect in a liquid layer[J]. Chinese Journal of Space Science, 2008, 28(1): 12-16 doi: 10.11728/cjss2008.01.012 [16] SHI W Y, RONG S M, FENG L. Marangoni convection instabilities induced by evaporation of liquid layer in an open rectangular pool[J]. Microgravity Science and Technology, 2017, 29(1): 91-96 [17] VILLERS D, PLATTEN J K. Separation of Marangoni convection from gravitational convection in earth experiments[J]. Physico Chemical Hydrodynamics, 1987, 8(2): 173-183 [18] GONG X W, MO D M, WU C M, et al. Linear-stability analysis of thermocapillary-buoyancy convection in annular two-layer system with a radial temperature gradient[J]. International Communications in Heat and Mass Transfer, 2015, 66: 58-62 doi: 10.1016/j.icheatmasstransfer.2015.03.003 [19] LI H M, SHI W Y. Thermocapillary convection in a differentially heated two-layer annular system with and without rotation[J]. International Journal of Heat and Mass Transfer, 2017, 105: 684-689 doi: 10.1016/j.ijheatmasstransfer.2016.10.038 [20] LIU Q S, ZHOU J Y, WANG A, et al. Thermovibrational instability of Rayleigh–Marangoni–Benard convection in two-layer fluid systems[J]. Advances in Space Research, 2008, 41(12): 2131-2136 doi: 10.1016/j.asr.2007.09.016 [21] ZHOU X M, HUANG H L. MHD effects on the instability of thermocapillary convection in two-layer fluid system[J]. International Journal of Heat and Mass Transfer, 2010, 53(25/26): 5827-5834 [22] SHIOMI J, KUDO M, UENO I, et al. Feedback control of oscillatory thermocapillary convection in a half-zone liquid bridge[J]. Journal of Fluid Mechanics, 2003, 496: 193-211 doi: 10.1017/S0022112003006323 [23] ANTONOW G N. Sur la tension superficially à la limited de deux couches[J]. Journal de Chimie Physique, 1907, 5: 372-385 doi: 10.1051/jcp/1907050372 [24] BEKEZHANOVA V B, FLIAGIN V M, GONCHAROVA O N, et al. Thermocapillary deformations of a two-layer system of liquids under laser beam heating[J]. International Journal of Multiphase Flow, 2020, 132: 103429 doi: 10.1016/j.ijmultiphaseflow.2020.103429 -
-
下载:
计量
- 文章访问数: 263
- HTML全文浏览量: 96
- PDF下载量: 29
-
被引次数:
0(来源:Crossref)
0(来源:其他)
