基于GBR方法的Kp指数预报模型
doi: 10.11728/cjss2024.06.2024-0011 cstr: 32142.14.cjss.2024-0011
-
焦琦融 女, 1993年10月出生于内蒙古呼和浩特, 现为北京航空航天大学博士研究生, 主要研究方向为太阳物理过程、空间天气预报等. E-mail: JiaoQirong@buaa.edu.cn -
张典钧 男, 1994年10月出生于北京市西城区, 现为北京航空航天大学讲师, 主要研究方向为空间物理、内磁层动力学等. E-mail: diandian@buaa.edu.cn
作者简介:
通讯作者:
Kp Index Forecast Model Based on GBR Method
-
摘要: 地磁Kp指数是空间天气预警的重要指标, 也是研究太阳风–磁层耦合的关键参数. 采用梯度提升回归(GBR)算法和随机森林(RF)两种机器学习方法, 构建了以太阳风、行星际磁场参数、历史Kp值和太阳黑子数据为输入的3 h 地磁 Kp指数预报模型. 预报结果表明, 两种方法均可提前1 h预报地磁Kp指数, 预测结果与观测值之间的相关系数为0.90, 其中GBR方法在均方根误差上表现出更好的效果, 均方根误差为0.56. Kp指数预报模型在太阳活动周不同相位的预测结果存在差异, 在活动周下降阶段模型预测结果与观测数据的相关系数更高. 比较了不同地磁扰动下模型的预测情况, 相比中等磁暴和超强磁暴, 模型对强磁暴(6≤Kp<7)的预报准确度最高.Abstract: The solar wind transports solar activity energy to interplanetary space, causing changes in the spatial structure of the Earth’s magnetosphere and causing disastrous space weather. The Kp index is an important indicator for space weather alerts and a key parameter for the coupling between solar wind and the magnetosphere. With the development of machine learning methods, more and more space weather forecasting works adopt this method. In this paper, two machine learning methods, Gradient Boosting Regression (GBR) algorithm and Random Forest (RF), are used to construct a 3-hour Kp index prediction model with solar wind, interplanetary magnetic field parameters, historical Kp values and sunspot data as inputs. The forecast results show that our methods can predict the Kp index one hour in advance and the correlation coefficient is 0.90 between the Kp index of the optimal case recommended by the model and the actual value. The GBR model performs better, the root Mean Square Error (Erms) is 0.56, and the Prediction Efficiency (P) is 0.81. The Kp index prediction model shows varying performances in different solar cycle phases, with better result during the cycle descending phase. The high-speed solar wind drive dominates the magnetospheric dynamics, and the model with solar wind as the main input parameter in the cycle descending phase has a better prediction effect. The model prediction situations under different geomagnetic disturbances have been compared. Compared with moderate and super severe magnetic storms, the model has the highest prediction accuracy for severe magnetic storms (6≤Kp<7). In this study, the results of different prediction models are compared and analyzed. The prediction model can not only provide early warning of severe space weather, but also better understand the relationship between geomagnetic index and solar wind input energy, which provides more methods and theoretical basis for the research work of solar wind-magnetosphere coupling.
-
Key words:
- Kp index /
- Machine learning /
- Space weather forecast
-
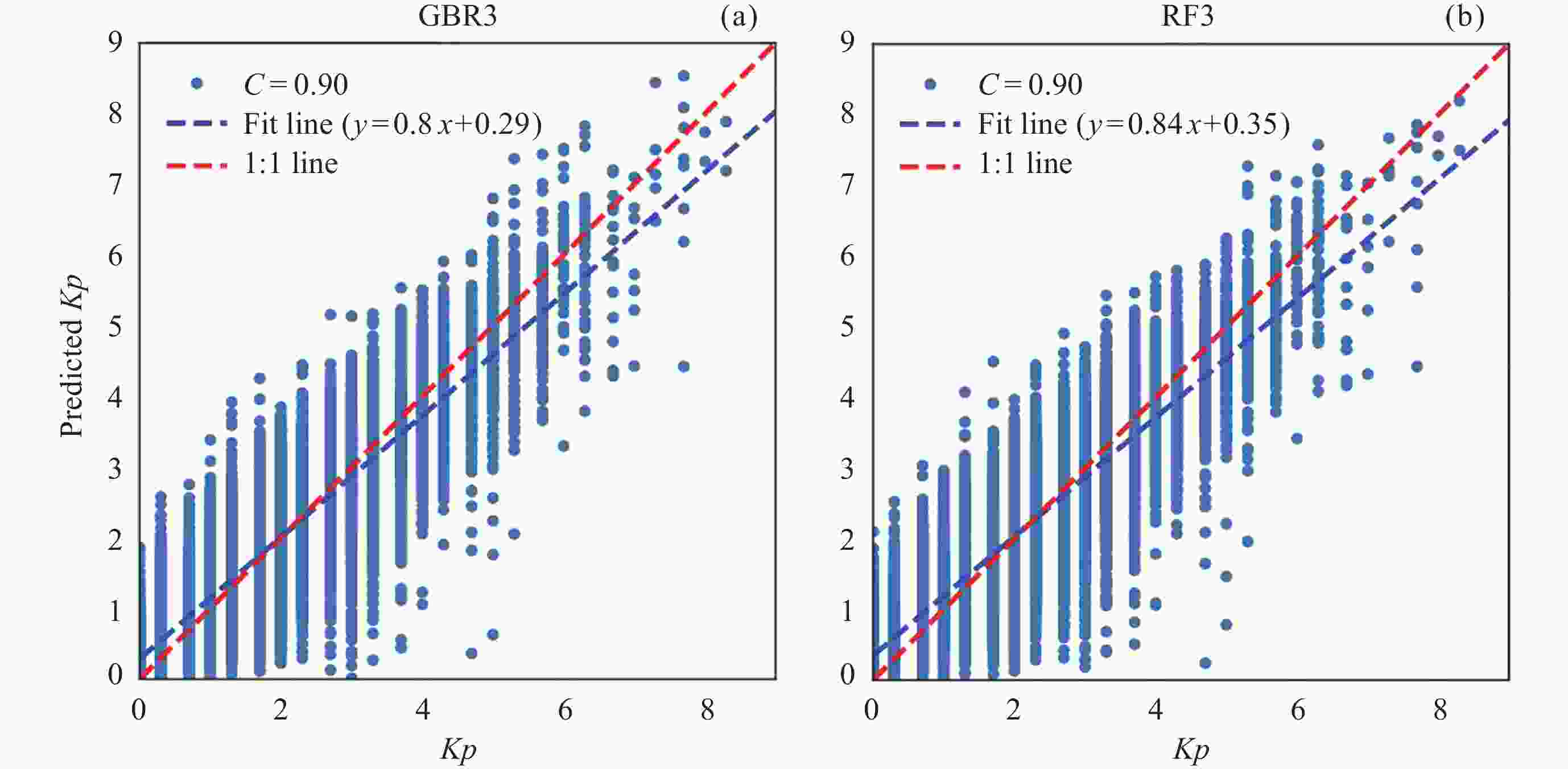
图 2 观测Kp值与GBR3和RF3模型的预测Kp值对比(红色虚线表示对角线, 蓝色虚线表示线性拟合直线相关系数为0.90)
Figure 2. Kp observations and predictions, with observed Kp values on the horizontal axis and predicted values on the vertical axis (The red dashed line represents the diagonal line, and the blue dashed line represents the linear fit result of the scatter, with a correlation coefficient of 0.90)
表 1 输入参数和3 h 地磁 Kp指数预测模型结果 (提前1 h)
Table 1. Data set variables and comparison of the prediction model results of 3-hour Kp index (predict 1 h)
模型名称 输入参数 C P Erms GBR1 vsw, Psw, Nsw, Bz, B, E 0.89 0.79 0.58 RF1 0.87 0.75 0.65 GBR2 vsw, Psw, Nsw, Bz, B, E, Kpt–3 0.90 0.81 0.56 RF2 0.89 0.79 0.59 GBR3 vw, Psw, Nsw, Bz, B, E, Kpt–3, Aall 0.90 0.81 0.56 RF3 0.90 0.80 0.58 注 Kpt–3 表示3 h 前Kp 指数. 
下载: 导出CSV
表 2 3 h地磁 Kp指数GBR预测模型与现有模型结果对比
Table 2. Comparison of the GBR prediction model of 3-hour Kp index with the existing models
下载: 导出CSV
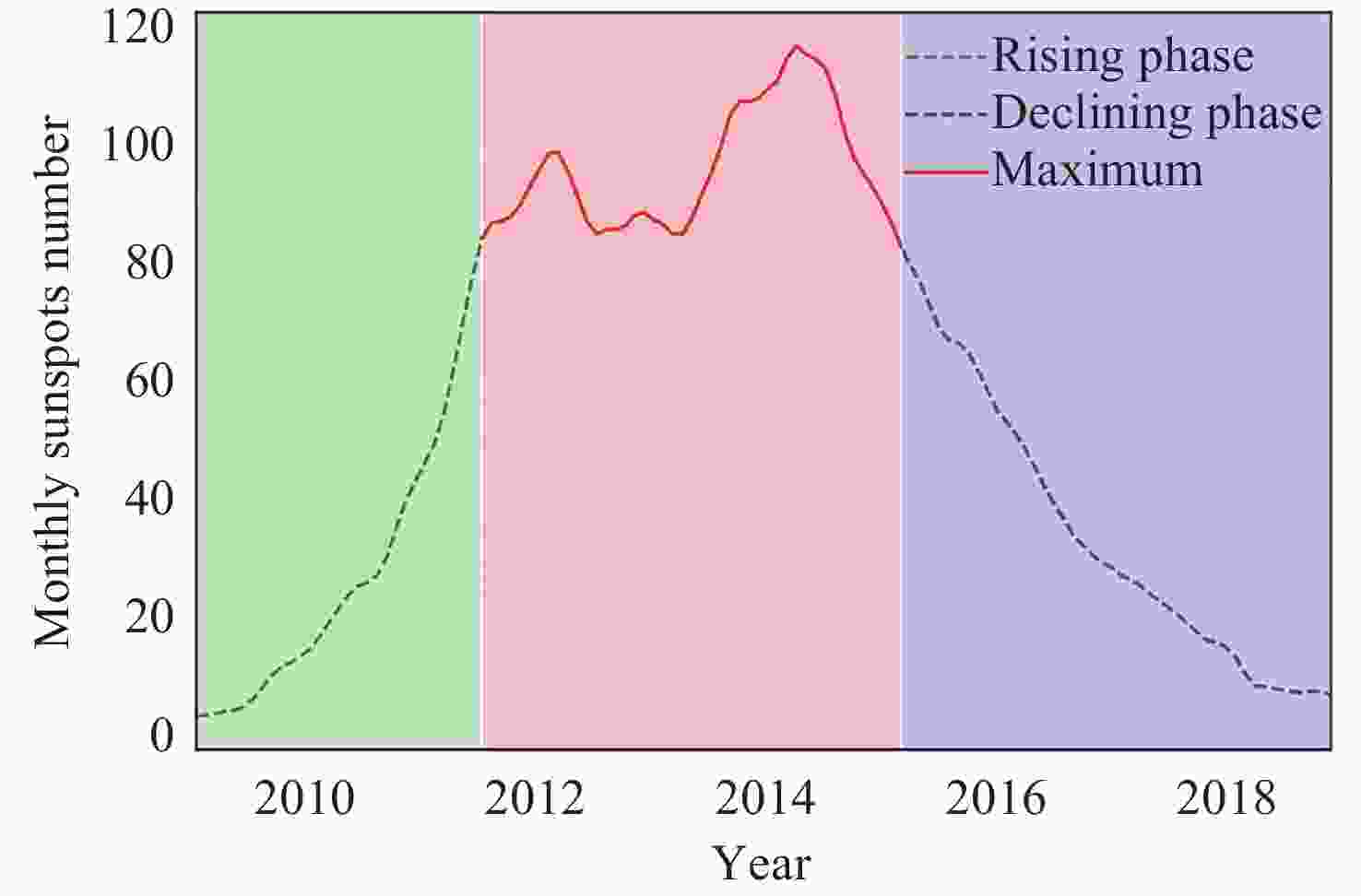
表 3 3 h模型在太阳活动周不同相位的预测结果相关系数
Table 3. Correlation coefficient during different solar cycle phase of the 3-hour prediction model
GBR1 RF1 GBR2 RF2 GBR3 RF3 上升阶段 0.89 0.88 0.89 0.88 0.89 0.88 极大期 0.88 0.87 0.89 0.88 0.89 0.88 下降阶段 0.89 0.89 0.90 0.89 0.90 0.90
下载: 导出CSV
表 4 不同地磁扰动情况下3 h地磁 Kp 指数预测结果
Table 4. Comparison of the prediction results of 3-hour Kp index under different geomagnetic disturbance
数据总数 预测次数 准确比例/(%) 5≤Kp<6 413 106 26 6≤Kp<7 104 36 35 Kp≥7 24 6 24
下载: 导出CSV
-
[1] CAO J B, DUAN J T, DU A M, et al. Characteristics of middle- to low-latitude Pi2 excited by bursty bulk flows[J]. Journal of Geophysical Research: Space Physics, 2008, 113(A7): A07S15 [2] CAO J B, YAN C X, DUNLOP M, et al. Geomagnetic signatures of current wedge produced by fast flows in a plasma sheet[J]. Journal of Geophysical Research: Space Physics, 2010, 115(A8): A08205 [3] . BARTELS J. The standardized index, Ks, and the planetary index Kp[J]. IATME Bull 12b, IUGG Publ Office, Paris 1949 : 97–112; reprinted in: IAGA Bull 12i, IUGG Publ Office, Paris 1955: 88–101 [4] TAKAHASHI K, TOTH B A, OLSON J V. An automated procedure for near-real-time Kp estimates[J]. Journal of Geophysical Research: Space Physics, 2001, 106(A10): 21017-21032 doi: 10.1029/2000JA000218 [5] LUO B, LIU S, GONG J. Two empirical models for short-term forecast of Kp[J]. Space Weather, 2017, 15(3): 503-516 doi: 10.1002/2016SW001585 [6] COSTELLO K A. Moving the Rice MSFM into A Real-Time Forecast Mode Using Solar Wind Driven Forecast Modules[D]. Houston: Rice University, 1998 [7] BALA R, REIFF P. Improvements in short-term forecasting of geomagnetic activity[J]. Space Weather, 2012, 10(6): S06001 [8] BALA R, REIFF P H, LANDIVAR J E. Real-time prediction of magnetospheric activity using the Boyle Index[J]. Space Weather, 2009, 7(4): S04003 [9] AYALA SOLARES J R, WEI H L, BOYNTON R J, et al. Modeling and prediction of global magnetic disturbance in near-earth space: a case study for Kp index using NARX models[J]. Space Weather, 2016, 14(10): 899-916 doi: 10.1002/2016SW001463 [10] WING S, JOHNSON J R, JEN J, et al. Kp forecast models[J]. Journal of Geophysical Research: Space Physics, 2005, 110(A4): A04203 [11] TAN Y, HU Q H, WANG Z, et al. Geomagnetic index Kp forecasting with LSTM[J]. Space Weather, 2018, 16(4): 406-416 doi: 10.1002/2017SW001764 [12] WANG J J, ZHONG Q Z, LIU S Q, et al. Statistical analysis and verification of 3-hourly geomagnetic activity probability predictions[J]. Space Weather, 2015, 13(12): 831-852 doi: 10.1002/2015SW001251 [13] 刘杨, 罗冰显, 刘四清, 等. 基于神经网络方法的Kp预报模型[J]. 载人航天, 2013, 19(2): 70-80 doi: 10.3969/j.issn.1674-5825.2013.02.011LIU Yang, LUO Bingxian, LIU Siqing, et al. Kp forecast models based on neural networks[J]. Manned Spaceflight, 2013, 19(2): 70-80 doi: 10.3969/j.issn.1674-5825.2013.02.011 [14] JOHNSON J R, WING S. A solar cycle dependence of nonlinearity in magnetospheric activity[J]. Journal of Geophysical Research: Space Physics, 2005, 110(A4): A04211 [15] LE G M, CAI Z Y, WANG H N, et al. Solar cycle distribution of great geomagnetic storms[J]. Astrophysics and Space Science, 2012, 339(1): 151-156 doi: 10.1007/s10509-011-0960-y [16] PERREAULT P, AKASOFU S I. A study of geomagnetic storms[J]. Geophysical Journal International, 1978, 54(2): 547-573 [17] KAN J R, LEE L C. Energy coupling function and solar wind-magnetosphere dynamo[J]. Geophysical Research Letters, 1979, 6(7): 577-580 doi: 10.1029/GL006i007p00577 [18] THOMSEN M F. Why Kp is such a good measure of magnetospheric convection[J]. Space Weather, 2004, 2(11): S11004 [19] BARGATZE L F, BAKER D N, MCPHERRON R L, et al. Magnetospheric impulse response for many levels of geomagnetic activity[J]. Journal of Geophysical Research: Space Physics, 1985, 90(A7): 6387-6394 doi: 10.1029/JA090iA07p06387 [20] 徐文耀. 太阳风–磁层–电离层耦合过程中的能量收支[J]. 空间科学学报, 2011, 31(1): 1-14 doi: 10.11728/cjss2011.01.001XU Wenyao. Energy budget in the coupling processes of the solar wind, magnetosphere and ionosphere[J]. Chinese Journal of Space Science, 2011, 31(1): 1-14 doi: 10.11728/cjss2011.01.001 [21] JIAO Q R, LIU W L, ZHANG D J, et al. Relation between latitude-dependent sunspot data and near-earth solar wind speed[J]. The Astrophysical Journal, 2023, 958(1): 70 doi: 10.3847/1538-4357/acfc21 [22] KING J H, PAPITASHVILI N E. Solar wind spatial scales in and comparisons of hourly wind and ACE plasma and magnetic field data[J]. Journal of Geophysical Research: Space Physics, 2005, 110(A2): A02104 [23] WOLF W. Abstract of his latest Results[J]. Monthly Notices of the Royal Astronomical Society, 1861, 21(3): 77-78 doi: 10.1093/mnras/21.3.77 [24] BIAU G, CADRE B, ROUVIÈRE L. Accelerated gradient boosting[J]. Machine Learning, 2019, 108(6): 971-992 doi: 10.1007/s10994-019-05787-1 [25] FRIEDMAN J H. Greedy function approximation: a gradient boosting machine[J]. The Annals of Statistics, 2001, 29(5): 1189-1232 doi: 10.1214/aos/1013203450 [26] NATEKIN A, KNOLL A. Gradient boosting machines, a tutorial[J]. Frontiers in Neurorobotics, 2013, 7: 21 [27] BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32 doi: 10.1023/A:1010933404324 [28] HE J S, MARSCH E, TU C Y, et al. Intermittent outflows at the edge of an active region: a possible source of the solar wind[J]. Astronomy & Astrophysics, 2010, 516: A14 doi: 10.1051/0004-6361/200913712 [29] KOJIMA M, FUJIKI K, OHMI T, et al. Low-speed solar wind from the vicinity of solar active regions[J]. Journal of Geophysical Research: Space Physics, 1999, 104(A8): 16993-17003 doi: 10.1029/1999ja900177 [30] ZANGRILLI L, POLETTO G. Evolution of active region outflows throughout an active region lifetime[J]. Astronomy & Astrophysics, 2016, 594: A40 doi: 10.1051/0004-6361/201628421 [31] FU H, LI B, LI X, et al. Coronal sources and in situ properties of the solar winds sampled by ACE during 1999-2008[J]. Solar Physics, 2015, 290(5): 1399-1415 doi: 10.1007/s11207-015-0689-9 [32] . BOBERG F, WINTOFT P, LUNDSTEDT H. Real time Kp predictions from solar wind data using neural networks[J]. Physics and Chemistry of the Earth, Part C: Solar, Terrestrial & Planetary Science, 2000, 25 (4): 275-280 [33] BERGIN A, CHAPMAN S C, MOLONEY N R, et al. Variation of geomagnetic index empirical distribution and burst statistics across successive solar cycles[J]. Journal of Geophysical Research: Space Physics, 2022, 127(1): e2021JA029986 doi: 10.1029/2021JA029986 [34] 张典钧, 刘文龙, 杜俊峰, 等. 行星际激波导致内磁层脉冲电场的模拟研究[J]. 地球物理学报, 2023, 66(11): 4429-4436 doi: 10.6038/cjg2022Q0701ZHANG Dianjun, LIU Wenlong, DU Junfeng, et al. Simulation study on the Impulsive Electric Field induced by an interplanetary shock[J]. Chinese Journal of Geophysics, 2023, 66(11): 4429-4436 doi: 10.6038/cjg2022Q0701 [35] SEXTON E S, NYKYRI K, MA X Y. Kp forecasting with a recurrent neural network[J]. Journal of Space Weather and Space Climate, 2019, 9: A19 doi: 10.1051/swsc/2019020 [36] 王子思禹, 师立勤, 刘四清, 等. 基于机器学习相似度算法的Kp指数预报[J]. 空间科学学报, 2022, 42(2): 199-205. DOI: 10.11728/cjss2022.02.210316030WANG Zisiyu, SHI Liqin, LIU Siqing, et al. Kp index prediction based on similarity algorithm of machine learning[J]. Chinese Journal of Space Science, 2022, 42(2): 199-205. DOI: 10.11728/cjss2022.02.210316030 [37] GONZALEZ W D, GONZALEZ A L C, TSURUTANI B T. Dual-peak solar cycle distribution of intense geomagnetic storms[J]. Planetary and Space Science, 1990, 38(2): 181-187 doi: 10.1016/0032-0633(90)90082-2 [38] CROOKER N U, GRINGAUZ K I. On the low correlation between long-term averages of solar wind speed and geomagnetic activity after 1976[J]. Journal of Geophysical Research: Space Physics, 1993, 98(A1): 59-62 doi: 10.1029/92JA01978 [39] PAPITASHVILI V O, PAPITASHVILI N E, KING J H. Solar cycle effects in planetary geomagnetic activity: analysis of 36-year long OMNI dataset[J]. Geophysical Research Letters, 2000, 27(17): 2797-2800 doi: 10.1029/2000GL000064 [40] GARRETT H B, DESSLER A J, HILL T W. Influence of solar wind variability on geomagnetic activity[J]. Journal of Geophysical Research, 1974, 79(31): 4603-4610 doi: 10.1029/JA079i031p04603 [41] LIU W, SARRIS T E, LI X, et al. Solar wind influence on Pc4 and Pc5 ULF wave activity in the inner magnetosphere[J]. Journal of Geophysical Research: Space Physics, 2010, 115(A12): A12201 [42] MAYAUD P N. Derivation, Meaning, and Use of Geomagnetic Indices[M]. Washington: American Geophysical Union, 1980 [43] ZHANG D J, LIU W L, DU J F, et al. Response of electric field in terrestrial magnetosphere to interplanetary shock[J]. The Astrophysical Journal, 2022, 938(1): 70 doi: 10.3847/1538-4357/ac90cc -
-
下载:
图(3) / 表(4)
计量
- 文章访问数: 726
- HTML全文浏览量: 184
- PDF下载量: 69
-
被引次数:
0(来源:Crossref)
0(来源:其他)
