TLE轨道反演大气密度精度评估
doi: 10.11728/cjss2025.03.2024-0060 cstr: 32142.14.cjss.2024-0060
-
任廷领 男, 1990年10月出生于山东省聊城市, 现为中国科学院国家空间科学中心助理研究员, 主要研究方向为热层大气密度反演与模型修正. E-mail: rentl@nssc.ac.cn -
罗冰显 男, 1981年11月出生, 现为中国科学院国家空间科学中心研究员、博士生导师, 中国科学院大学岗位教授, 国家青年人才计划获得者, 主要研究方向为空间天气和空间环境的预报与应用. E-mail: luobx@nssc.ac.cn
作者简介:
通讯作者:
Accuracy Assessment of the TLE-derived Orbital Atmospheric Densities
-
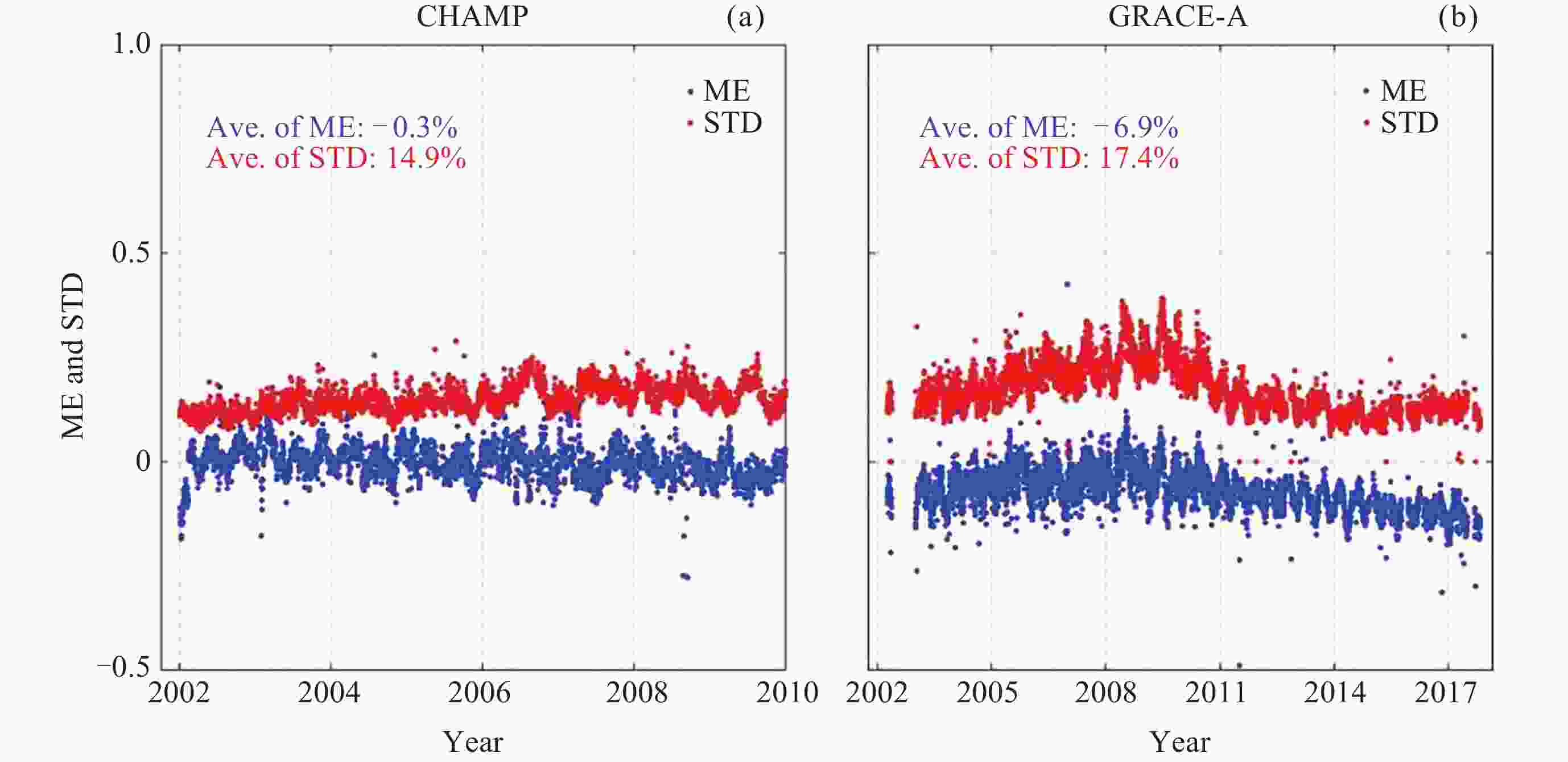
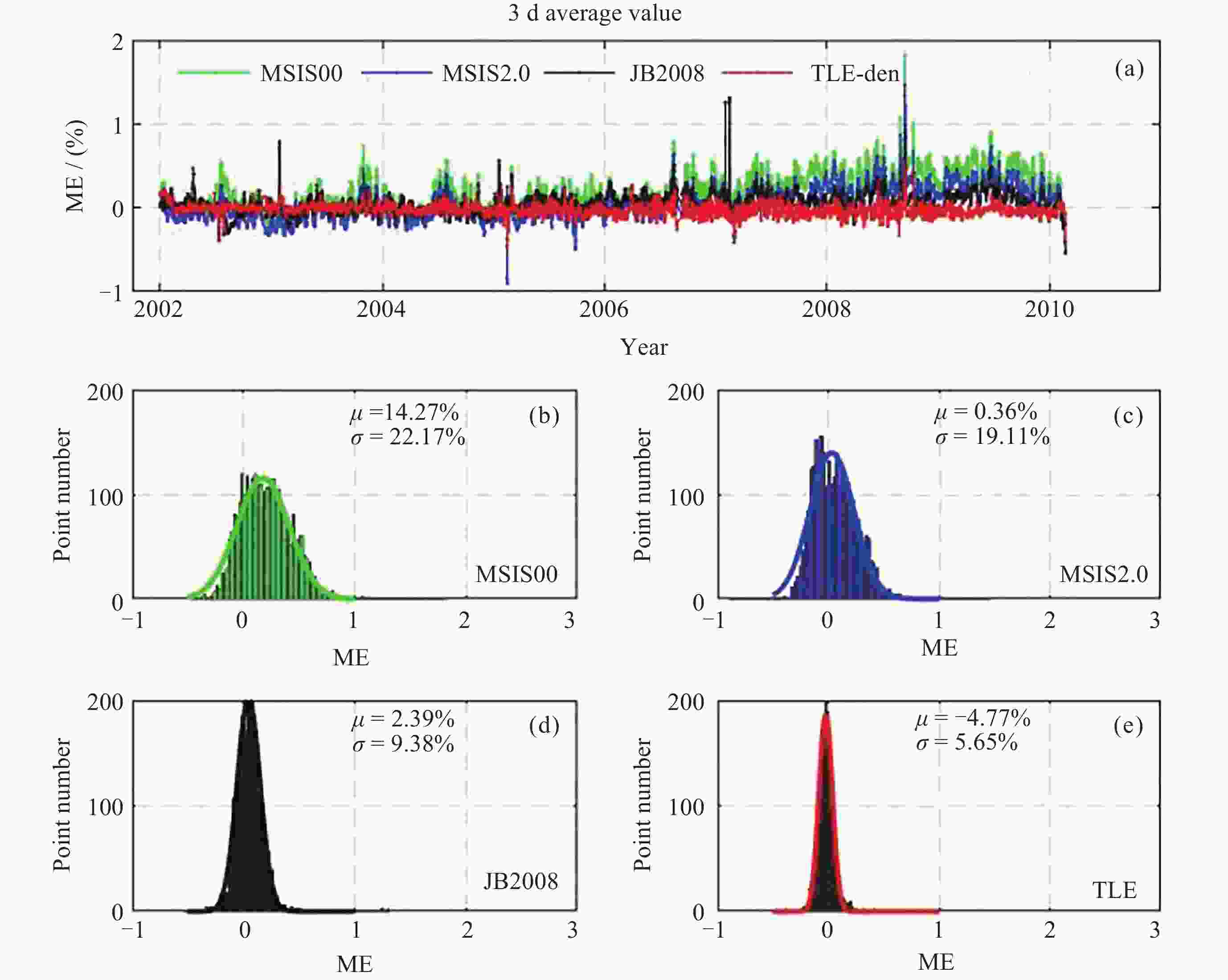
摘要: 利用CHAMP和GRACE-A卫星的TLE数据进行轨道大气密度反演, 并以高精度加速度仪密度作为基准计算反演密度误差, 同时与NRLMSISE-00, JB2008, MSIS2.0大气模式误差进行对比, 给出了TLE反演误差相对大气模式误差改善率的量化结果, 为TLE反演密度的准确性及实际应用提供了一定的理论支撑. 选取的TLE数据覆盖2002－2017年, 分别计算了两类密度反演值: TLE平均密度和TLE修正密度. 前者为时间分辨率为3 d的平均轨道大气密度, 该值不依赖于大气模式; 后者则是通过对大气模式进行修正得到的轨道原位处的大气密度. 结果表明, 在所分析的时间范围内, TLE平均密度的整体平均误差小于5%, 标准差小于8%; TLE修正密度在地磁平静期误差最小, 相对于大气模式的误差改善率超过80%.Abstract: In this research, we derived TLE-based atmospheric densities along CHAMP and GRACE-A orbits, and the density errors were calculated based on the high-accuracy accelerometer densities, empirical models errors including NRLMSISE-00, JB2008 and MSIS2.0 were also estimated for comparison. Improvement ratios, which defined as the percentage of TLE density errors smaller than that of empirical models, were given in the subsequent contents, and lay a theoretical foundation for the accuracy and application of the TLE-derived densities. TLE data ranged from 2002 to 2017, and two different kinds of densities, including TLE-averaged and TLE-calibrated densities, were derived. The former ones have a temporal resolution of 3 days, and were independent of the empirical models; the latter ones were calibrated values which relies on the empirical models. Results indicate that the TLE-averaged densities have a general average error smaller than 5%, and a standard deviation no bigger than 8%; the TLE-calibrated densities have the minimum errors during geomagnetic quiet conditions, with the improvement ratios bigger than 80%.
-
Key words:
- TLE-derived densities /
- Improvement ratios /
- Empirical atmospheric models
-
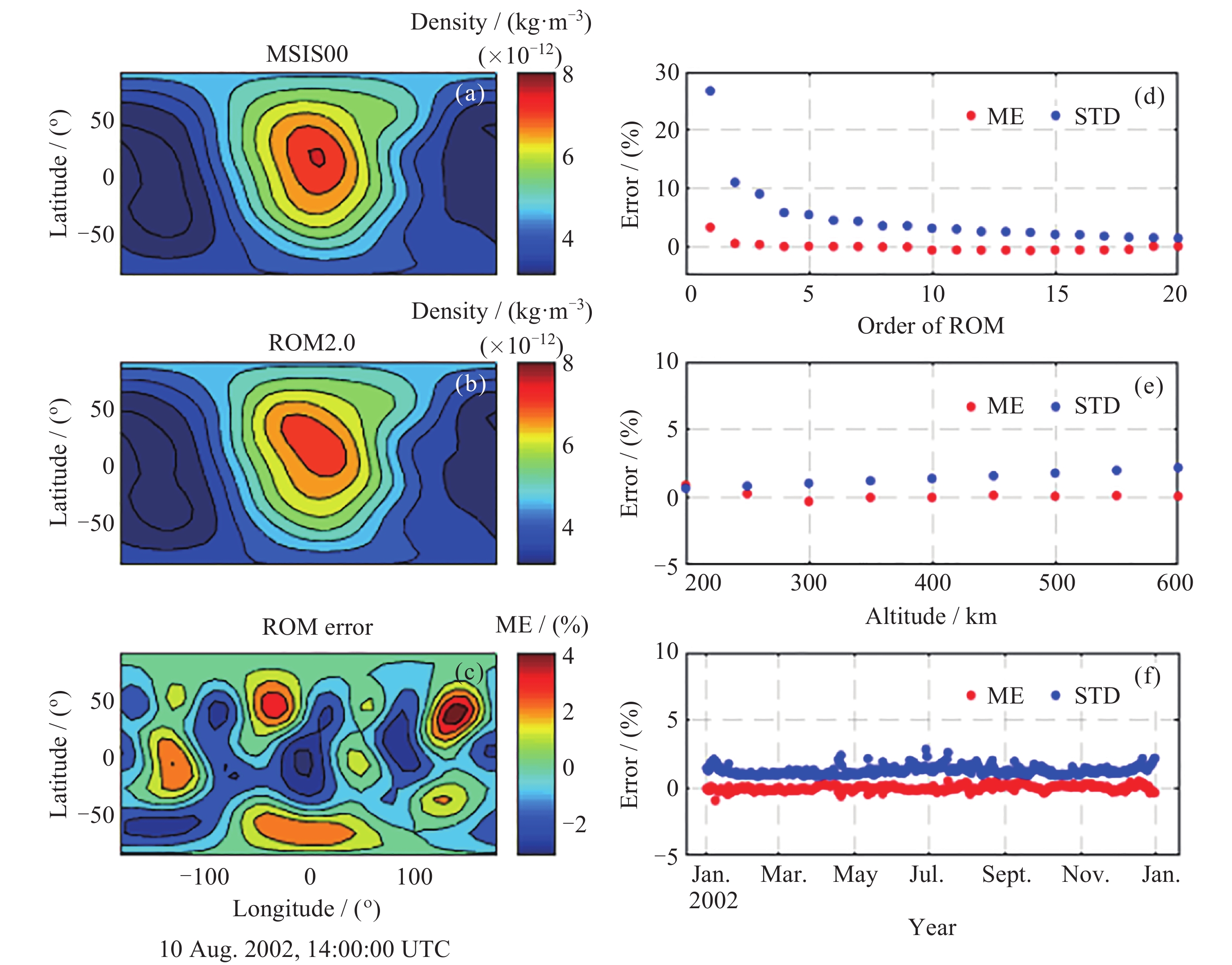
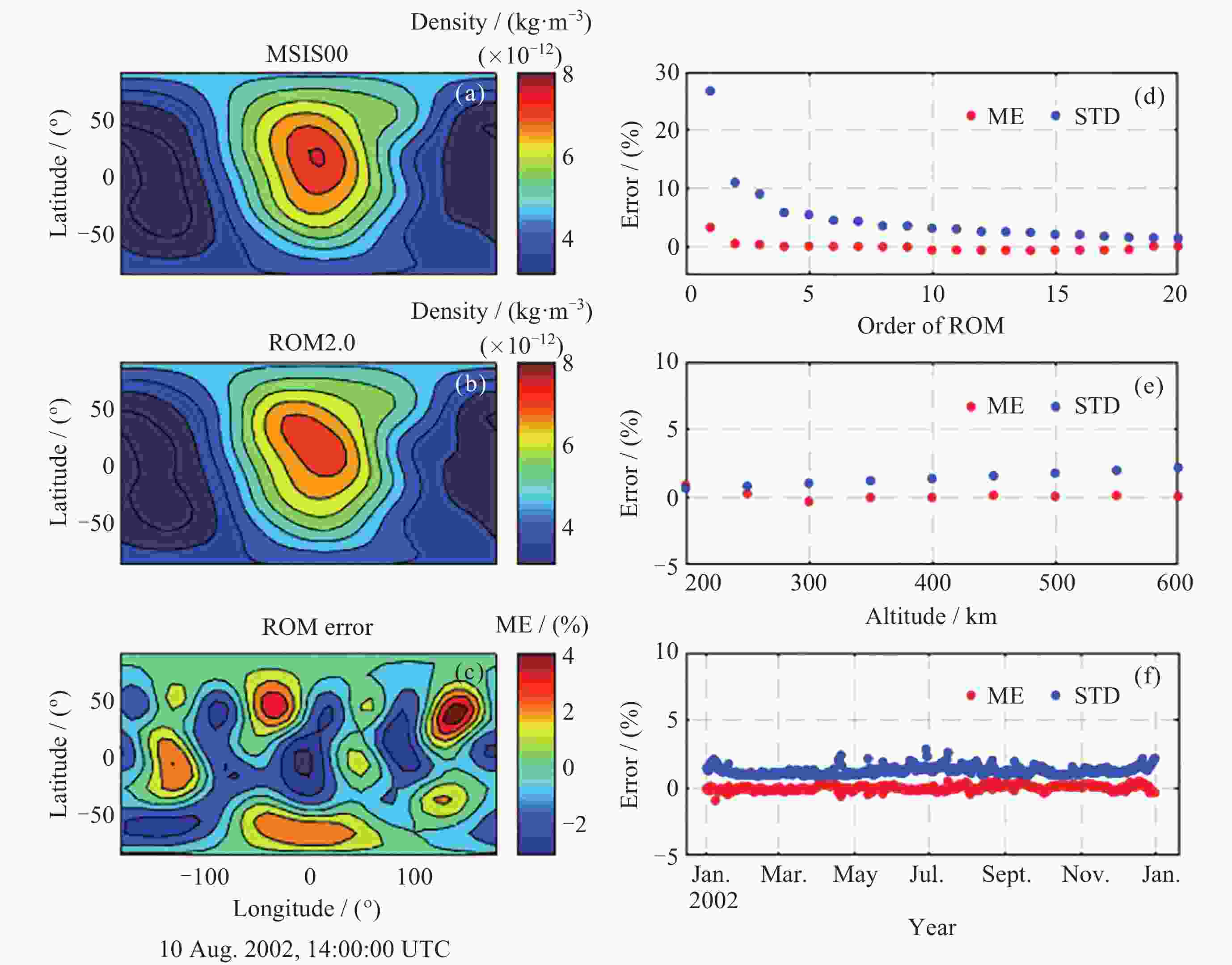
图 1 ROM模式精度分析. (a) MSIS00模式的全球分布, (b) 20阶ROM模型的全球密度分布, (c) ROM全球分布误差, (d)～(f) ROM误差随阶数、高度和时间的变化
Figure 1. Accuracy of the Reduced Order Model (ROM). (a) Global distribution of MSIS00 densities, (b) global density distribution of the 20th-order ROM Model, (c) global distribution of ROM error, (d)～(f) variation of errors with orders, altitude and time, respectively
图 3 CHAMP卫星TLE数据反演密度与模式密度误差对比
Figure 3. Comparison between TLE-derived and model density errors for CHAMP
图 4 GRACE-A卫星TLE数据反演密度与模式密度误差对比
Figure 4. Comparison between TLE-derived and model errors for GRACE-A
图 5 2002－2017年不同地磁条件事例筛选. 共筛选239个磁静日、 364个小磁暴日、73个中磁暴日和10个大磁暴日
Figure 5. Selection of cases with different geomagnetic conditions from 2002 to 2017. 239 geomagnetic quiet days, 364 minor storm days, 73 middle storm days and 10 major storm days are selected
图 6 CHAMP卫星TLE修正密度误差与模式误差的对比
Figure 6. Comparison between TLE-calibrated and model errors for CHAMP
图 7 GRACE-A卫星TLE修正密度误差与模式误差的对比
Figure 7. Comparison between TLE-calibrated and model errors for GRACE-A
表 1 ROM模式网格化设置
Table 1. Gridding settings of ROM model
项目 范围 分辨率 纬度/(°) [–90, 90] 10 经度/(°) [–180, 180] 10 高度/km [200, 600] 20 时间/year [2002, 2020] 1 
下载: 导出CSV
表 2 CHAMP卫星TLE修正密度误差改善率
Table 2. Ratio of the CHAMP TLE-calibrated density error improvement with that by models
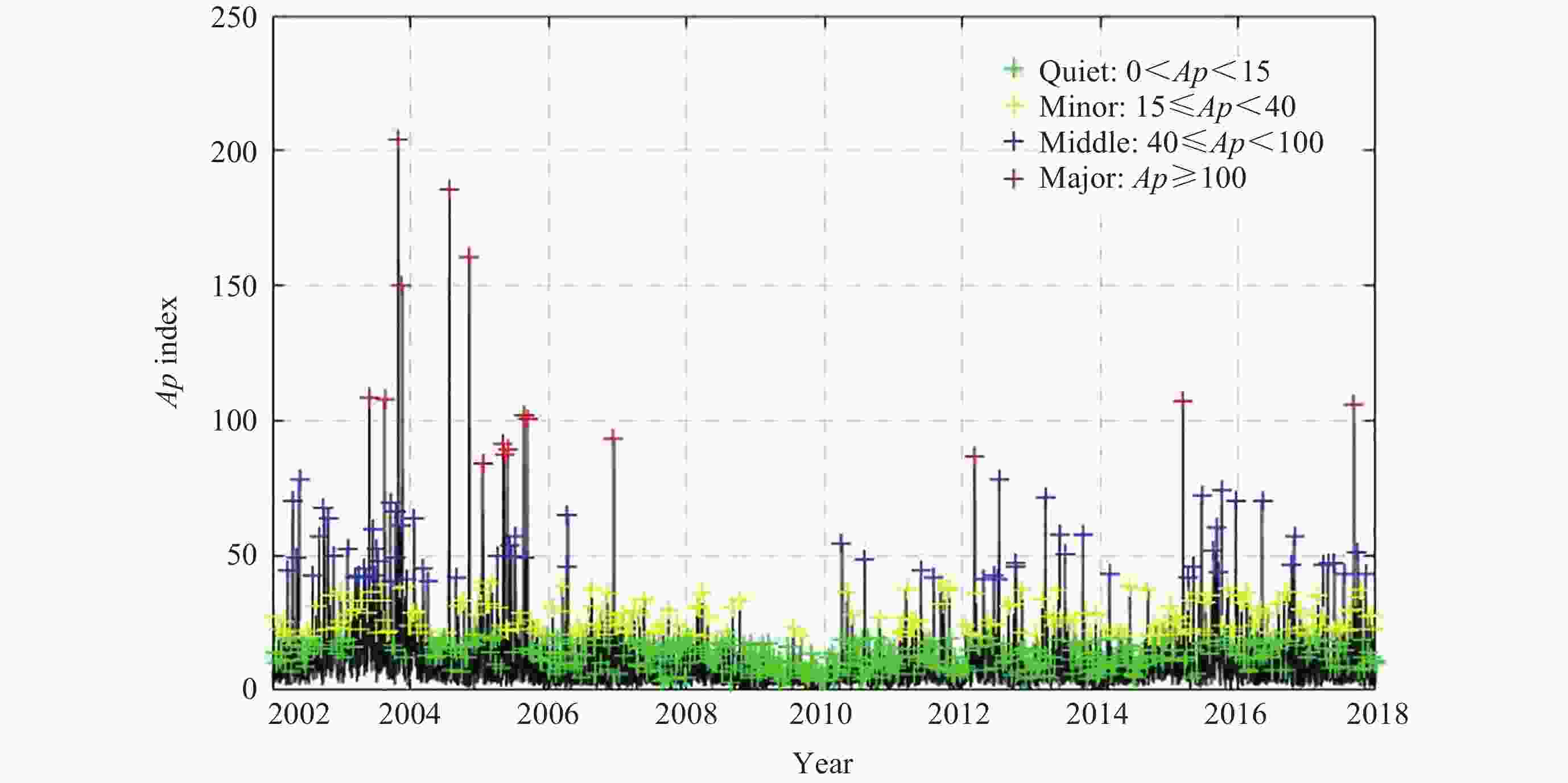
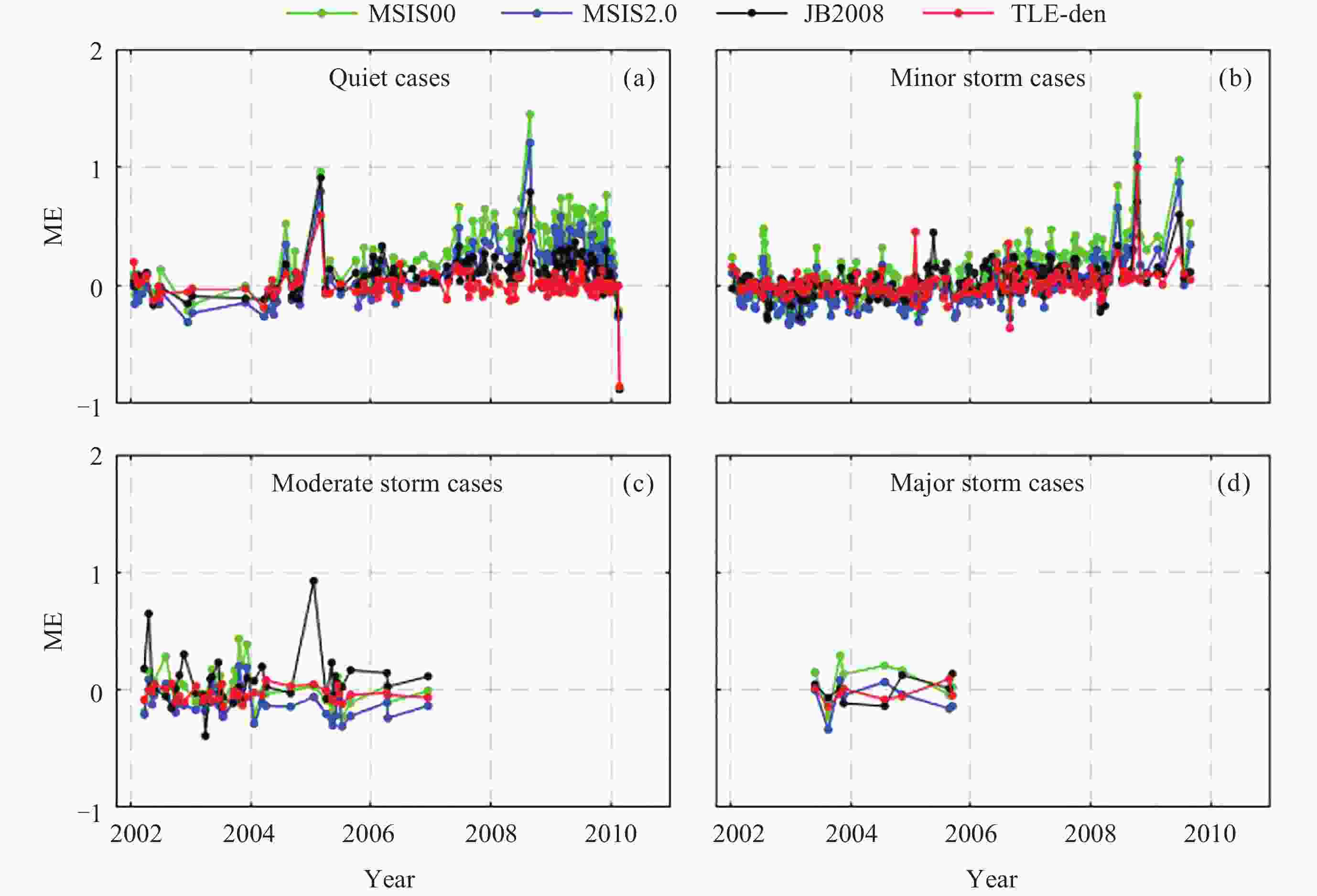
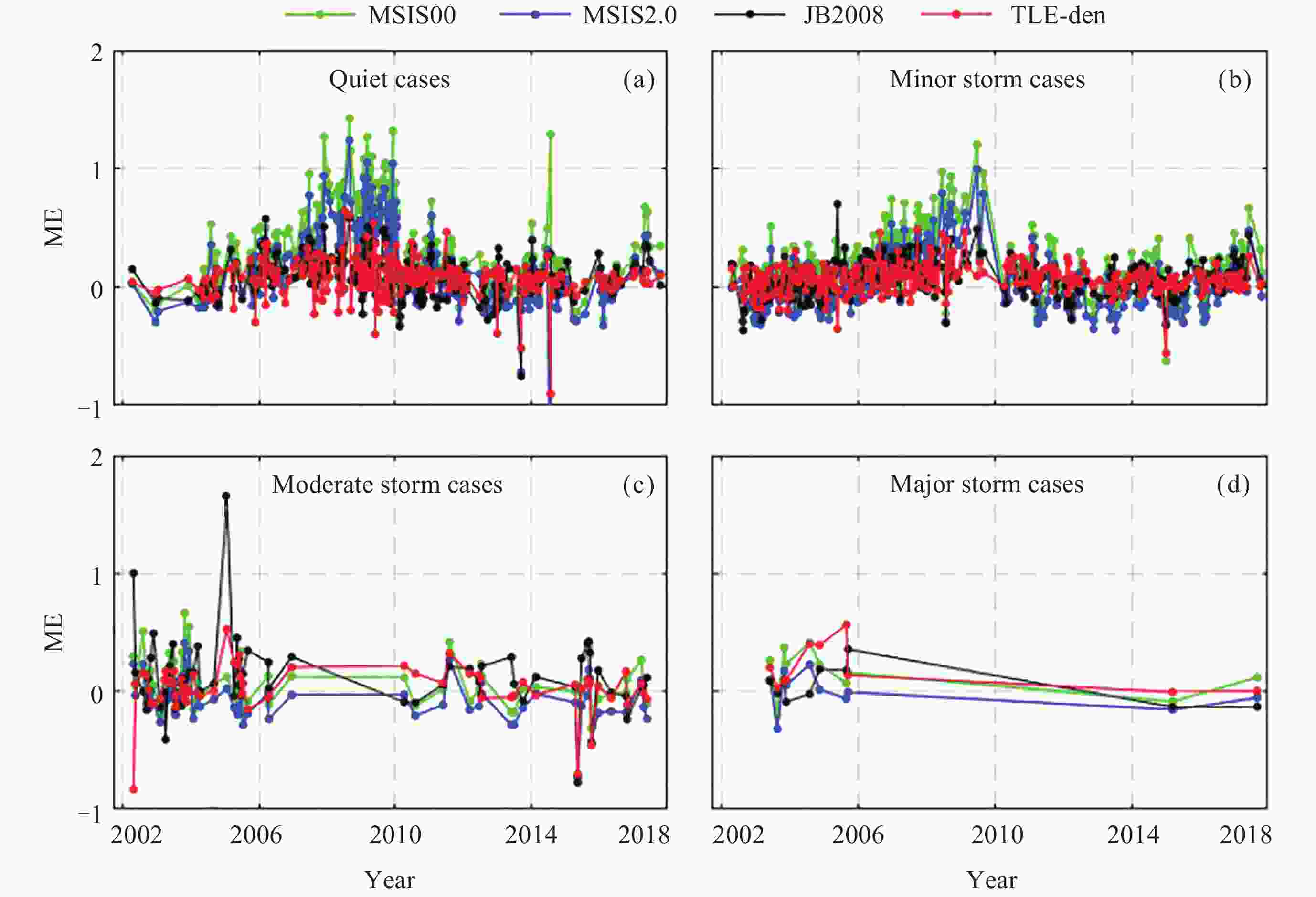
类型 $ r\left({\varepsilon }_{\mathrm{t}\mathrm{l}\mathrm{e}} < {\varepsilon }_{\mathrm{M}\mathrm{S}\mathrm{I}\mathrm{S}00}\right)/( $%) $ r\left({\varepsilon }_{\mathrm{t}\mathrm{l}\mathrm{e}} < {\varepsilon }_{\mathrm{M}\mathrm{S}\mathrm{I}\mathrm{S}2.0}\right)/( $%) $ r\left({\varepsilon }_{\mathrm{t}\mathrm{l}\mathrm{e}} < {\varepsilon }_{\mathrm{J}\mathrm{B}2008}\right)/( $%) 磁静日 88.6 83.2 75.6 小磁暴 77.6 75.4 62.3 中磁暴 67.5 87.5 62.5 大磁暴 75.0 62.5 62.5
下载: 导出CSV
表 3 GRACE-A卫星TLE修正密度误差改善率
Table 3. Ratio of the GRACE-A TLE-derived density error improvement with that by models
类型 $ r\left({\varepsilon }_{\mathrm{t}\mathrm{l}\mathrm{e}} < {\varepsilon }_{\mathrm{M}\mathrm{S}\mathrm{I}\mathrm{S}00}\right)/( $%) $ r\left({\varepsilon }_{\mathrm{t}\mathrm{l}\mathrm{e}} < {\varepsilon }_{\mathrm{M}\mathrm{S}\mathrm{I}\mathrm{S}2.0}\right)/( $%) $ r\left({\varepsilon }_{\mathrm{t}\mathrm{l}\mathrm{e}} < {\varepsilon }_{\mathrm{J}\mathrm{B}2008}\right)/( $%) 磁静日 80.0 71.3 53.2 小磁暴 76.8 66.3 54.9 中磁暴 57.8 56.3 67.2 大磁暴 80.0 40.0 40.0
下载: 导出CSV
-
[1] PICONE J M, EMMERT J T, LEAN J L. Thermospheric densities derived from spacecraft orbits: accurate processing of two-line element sets[J]. Journal of Geophysical Research: Space Physics, 2005, 110(A3): A03301 [2] 许晓丽, 熊永清. 基于历史TLE的空间目标轨道预报误差演化规律研究[J]. 天文学报, 2019, 60(4): 30-1-30-13XU Xiaoli, XIONG Yongqing. Study on orbit prediction error of space objects based on historical TLE[J]. Acta Astronomica Sinica, 2019, 60(4): 30-1-30-13 [3] BOWMAN B R, TOBISKA W K, MARCOS F A, et al. A new empirical thermospheric density model JB2008 using new solar and geomagnetic indices[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Honolulu: AIAA, 2008 [4] BRUINSMA S, BONIFACE C. The operational and research DTM-2020 thermosphere models[J]. Journal of Space Weather and Space Climate, 2021, 11: 47 doi: 10.1051/swsc/2021032 [5] EMMERT J T, DROB D P, PICONE J M, et al. NRLMSIS 2.0: a whole-atmosphere empirical model of temperature and neutral species densities[J]. Earth and Space Science, 2021, 8(3): e2020EA001321 doi: 10.1029/2020EA001321 [6] 任廷领, 苗娟, 刘四清, 等. 利用卫星两行轨道根数反演热层密度[J]. 空间科学学报, 2014, 34(4): 426-433 doi: 10.11728/cjss2014.04.426REN Tingling, MIAO Juan, LIU Siqing, et al. Research on thermospheric densities derived from two-line element sets[J]. Chinese Journal of Space Science, 2014, 34(4): 426-433 doi: 10.11728/cjss2014.04.426 [7] GONDELACH D J, LINARES R. Real-time thermospheric density estimation via two-line element data assimilation[J]. Space Weather, 2020, 18(2): e2019SW002356 doi: 10.1029/2019SW002356 [8] EMMERT J T, DHADLY M S, SEGERMAN A M. A globally averaged thermospheric density data set derived from two-line orbital element sets and special perturbations state vectors[J]. Journal of Geophysical Research: Space Physics, 2021, 126(8): e2021JA029455 doi: 10.1029/2021JA029455 [9] DOORNBOS E, KLINKRAD H, VISSER P. Use of two-line element data for thermosphere neutral density model calibration[J]. Advances in Space Research, 2008, 41(7): 1115-1122 doi: 10.1016/j.asr.2006.12.025 [10] BERNSTEIN V, PILINSKI M, SUTTON E. Assessing thermospheric densities derived from orbital drag data[C]//31st AAS/AIAA Space Flight Mechanics Meeting. Austin, Texas: AIAA, 2023 [11] PICONE J M, HEDIN A E, DROB D P, et al. NRLMSISE-00 empirical model of the atmosphere: statistical comparisons and scientific issues[J]. Journal of Geophysical Research: Space Physics, 2002, 107(A12): SIA 15-1-SIA 15-16 [12] PICONE J M, EMMERT J T, LEAN J L. Thermospheric densities derived from spacecraft orbits: Accurate processing of two-line element sets[J]. Journal of Geophysical Research: Space Physics, 2005, 110(A3): A03301 [13] REN T L, LIU S Q, MIAO J, et al. Effects of geomagnetic storms on the accuracy of orbit-derived atmospheric density measurements[J]. Advances in Space Research, 2022, 70(10): 2818-2829 doi: 10.1016/j.asr.2022.09.036 [14] BOWMAN B R. True satellite ballistic coefficient determination for HASDM[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Monterey: AIAA, 2002 [15] EMMERT J T, MEIER R R, PICONE J M, et al. Thermospheric density 2002-2004: TIMED/GUVI dayside limb observations and satellite drag[J]. Journal of Geophysical Research: Space Physics, 2006, 111(A10): A10S16 [16] LEAN J L, PICONE J M, EMMERT J T, et al. Thermospheric densities derived from spacecraft orbits: application to the Starshine satellites[J]. Journal of Geophysical Research: Space Physics, 2006, 111(A4): A04301 [17] LU Z J, HU W D. Estimation of ballistic coefficients of space debris using the ratios between different objects[J]. Chinese Journal of Aeronautics, 2017, 30(3): 1204-1216 doi: 10.1016/j.cja.2017.03.009 [18] REIGBER C, LÜHR H, SCHWINTZER P. CHAMP mission status[J]. Advances in Space Research, 2002, 30(2): 129-134 doi: 10.1016/S0273-1177(02)00276-4 [19] TAPLEY B D, BETTADPUR S, WATKINS M, et al. The gravity recovery and climate experiment: mission overview and early results[J]. Geophysical Research Letters, 2004, 31(9): L09607 [20] ZAGLAUER A. Swarm satellites status[C]//ESA’s Second Swarm International Science Meeting. Potsdam, Germany: GFZ, 2009 [21] BRUINSMA S, FORBES J M, NEREM R S, et al. Thermosphere density response to the 20-21 November 2003 solar and geomagnetic storm from CHAMP and GRACE accelerometer data[J]. Journal of Geophysical Research: Space Physics, 2006, 111(A6): A06303 [22] CALABIA A, TANG G S, JIN S G. Assessment of new thermospheric mass density model using NRLMSISE-00 model, GRACE, Swarm-C, and APOD observations[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2020, 199: 105207 doi: 10.1016/j.jastp.2020.105207 [23] LEI J H, MATSUO T, DOU X K, et al. Annual and semiannual variations of thermospheric density: EOF analysis of CHAMP and GRACE data[J]. Journal of Geophysical Research: Space Physics, 2012, 117(A1): A01310 [24] BRUINSMA S L, DOORNBOS E, BOWMAN B R. Validation of GOCE densities and evaluation of thermosphere models[J]. Advances in Space Research, 2014, 54(4): 576-585 doi: 10.1016/j.asr.2014.04.008 [25] TOBISKA W K, BOWMAN B R, BOUWER S D, et al. The SET HASDM density database[J]. Space Weather, 2021, 19(4): e2020SW002682 doi: 10.1029/2020SW002682 [26] MATSUO T, RICHMOND A D, NYCHKA D W. Modes of high-latitude electric field variability derived from DE-2 measurements: empirical Orthogonal Function (EOF) analysis[J]. Geophysical Research Letters, 2002, 29(7): 1107 [27] MATSUO T, FORBES J M. Principal modes of thermospheric density variability: empirical orthogonal function analysis of CHAMP 2001-2008 data[J]. Journal of Geophysical Research: Space Physics, 2010, 115(A7): A07309 -
-
下载:
计量
- 文章访问数: 373
- HTML全文浏览量: 48
- PDF下载量: 33
-
被引次数:
0(来源:Crossref)
0(来源:其他)
