引入时间变量的TLE轨道确定
doi: 10.11728/cjss2025.05.2024-0130 cstr: 32142.14.cjss.2024-0130
-
刘劲宏 男, 1990年1月出生于四川省达州市, 现为重庆交通大学智慧城市学院讲师, 硕士生导师, 主要研究方向为空间碎片、空间气象等. E-mail: liu-jh@whu.edu.cn
作者简介:
TLE Orbit Determination Considering Time Variables
-
摘要: 利用TLE数据获得空间碎片的精确轨道信息一直是研究重点. 因缺乏对热层大气的理解, 大气阻力是轨道确定最大的误差来源, 其中大气密度模型、弹道系数中的误差与时间有关, 然而现有基于TLE数据的定轨算法并未考虑与时间相关的误差影响, 导致轨道预报精度无法进一步提升. 因此, 引入时间变量, 利用单纯形调优搜索算法将其与其他轨道参数一同求解, 削弱与时间相关的误差对轨道精度的影响. 使用8颗卫星的TLE数据和CPF精密星历数据开展实验, 引用时间变量的轨道预报相对精度提升了0.11%～78.60%. 因此, 通过引入时间变量削弱与时间变量相关的误差, 有助于提升定轨精度, 研究成果有望在大气再入预报、风险评估、碰撞预警等领域得到应用.Abstract: To obtain precise orbit information of space debris from Two-Line Element (TLE) has always been a research focus. Due to a lack of understanding of the thermosphere atmosphere, atmospheric drag is the largest source of error in orbit determination, with errors in atmospheric density models and trajectory coefficients being time-dependent. However, TLE-based orbit determination algorithms have not taken into account the impact of time-dependent errors, resulting in the inability to further improve orbit prediction accuracy. Therefore, this article introduces a time variable and uses the simplex optimization search algorithm to solve it together with other orbit parameters, weakening the impact of time-related errors on orbit accuracy. This article conducted experiments using TLE data and CPF (Consolidated Prediction Format) precise ephemeris data from 8 satellites, and the relative accuracy of orbit prediction considering time variables was improved by 0.11%～78.60%. Therefore, introducing time variables to weaken errors related to time variables can help improve orbit determination accuracy, and research results are expected to be applied in fields, such as atmospheric re-entry forecasting, risk assessment, collision warning, etc.
-
Key words:
- Two-line element /
- Orbital determination /
- Orbital prediction /
- Simplex method
-
图 1 基于SM和TSM的目标函数值分布(卫星31698)
Figure 1. Distribution of the object function based on SM and TSM (Satellite 31698)
图 2 原始TLE, SM, TSM定轨结果的轨道预报误差的比较
Figure 2. Orbital error predictions of primeval TLE, SM and TSM in RSW coordinate system
图 3 TLE, SM和TSM的轨道预报误差
Figure 3. Comparisons of the orbital prediction errors from TLE, SM and TSM
图 4 RSW坐标系下的轨道预报标准差
Figure 4. Standard deviation of orbit prediction in RSW coordinate system
表 1 卫星轨道类型与高度参数
Table 1. Satellite orbital types and altitude parameters
NORAD 卫星名 轨道类型 近地点/km 远地点/km 31698 TERRA SAR X LEO 507 510 39452 SWARM A LEO 444 447 40001 COSMOS 2500 (GLONASS) MEO 19118 19142 41240 JASON 3 LEO 1332 1344 43687 COSMOS 2529 (GLONASS) MEO 19109 19151 46805 COSMOS 2547 (GLONASS) MEO 19113 19147 46808 YAOGAN-30 V LEO 568 571 46984 S6 MICHAEL FREILICH LEO 1332 1344 
下载: 导出CSV
表 2 定轨TLE历元剔除比例
Table 2. Eliminating ratio of reference epoch for orbit determination TLE
NORAD 原始TLE历元数 异常TLE历元数 TLE历元使用率/(%) 31698 29 3 89.65 39452 22 0 100 40001 17 0 100 41240 18 0 100 43687 17 2 88.23 46805 16 0 100 46808 15 2 86.67 46984 31 4 87.09
下载: 导出CSV
表 3 目标31698定轨轨道根数对比
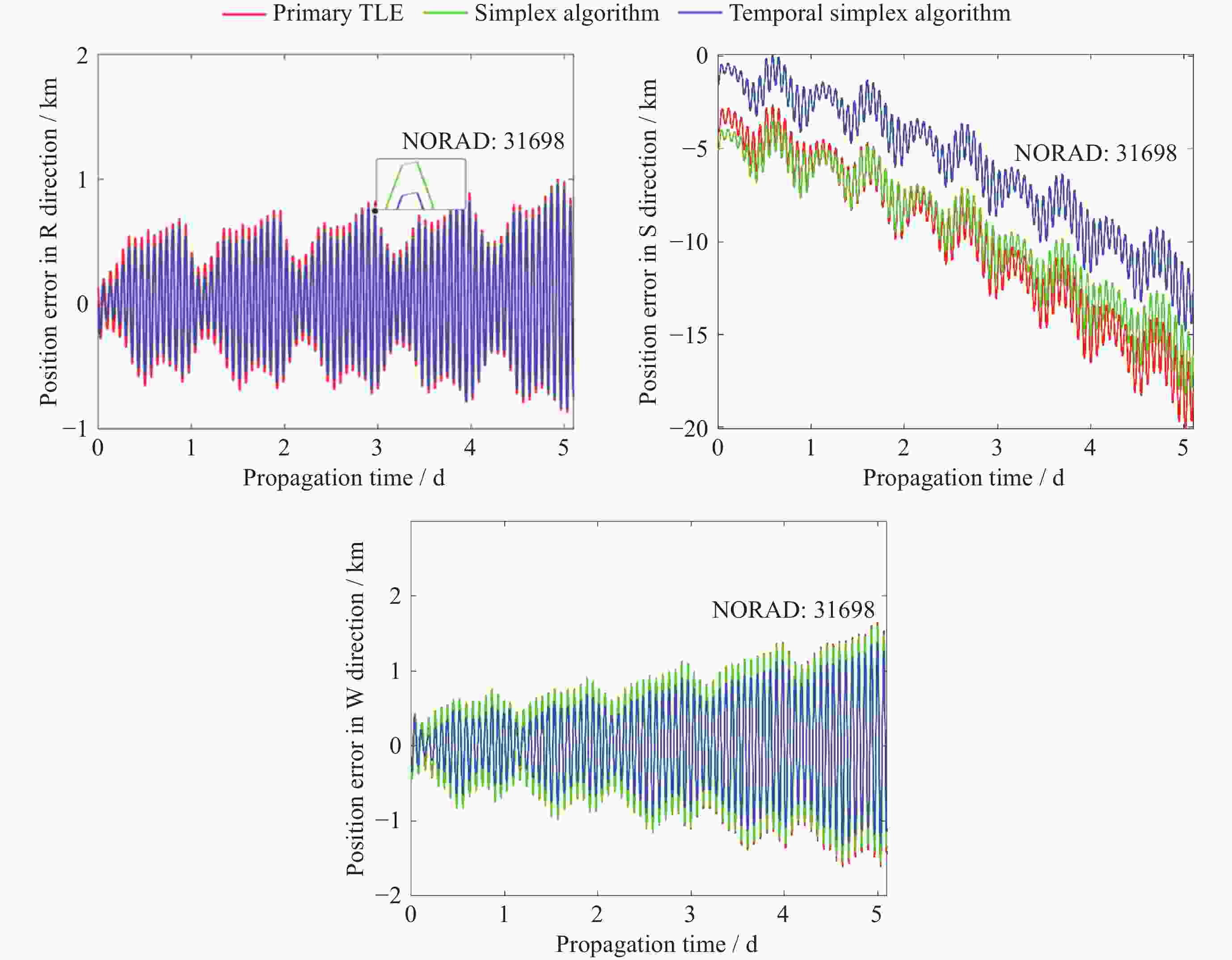
Table 3. Comparison of the orbital elements of the target 31698
算法 $ {B}' $ $ e $ $ i $ /(°) $ {\varOmega} $ /(°) $ \omega $ /(°) $ M $ /(°) $ n $ /(rev·d–1) 定轨结果时刻数据 TLE 7.5814×10–6 2.147×10–4 97.4459 10.8697 17.0107 77.2867 15.19153825 21365.87937972 SM 3.1545×10–5 1.950×10–4 97.4458 10.8702 17.5800 76.7078 15.19155608 21365.87937972 TSM 3.1551×10–5 1.950×10–4 97.4458 10.8701 16.5589 77.1212 15.19155551 21365.87835189 注 $ {B}' $表示弹道系数, $ e $ 表示偏心率, $ i $表示轨道倾角, $ {\varOmega} $表示升交点赤经, $ \omega $表示平近点角, $ M $表示近地点角距, $ n $表示平运动.
下载: 导出CSV
表 4 卫星轨道预报标准差
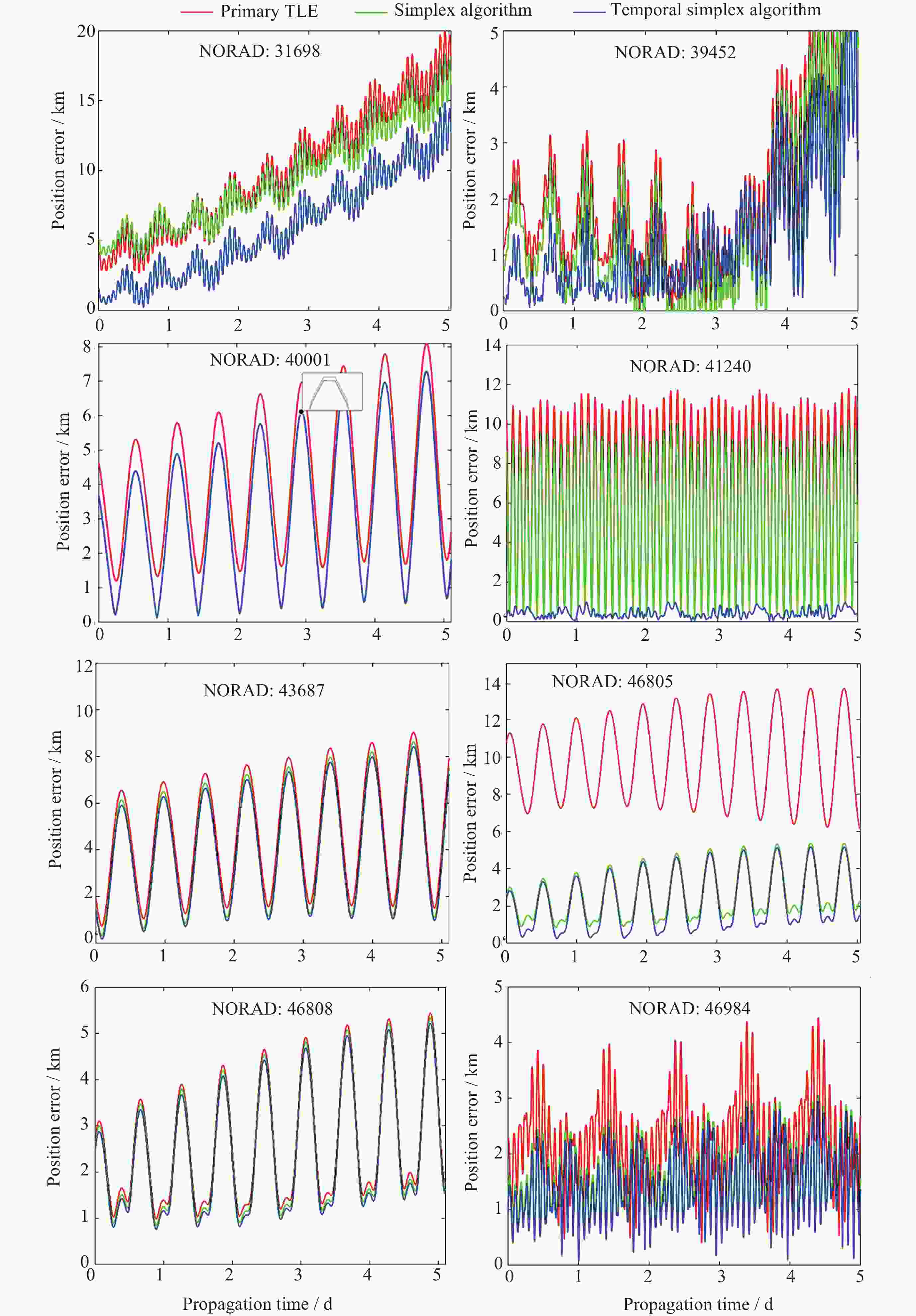
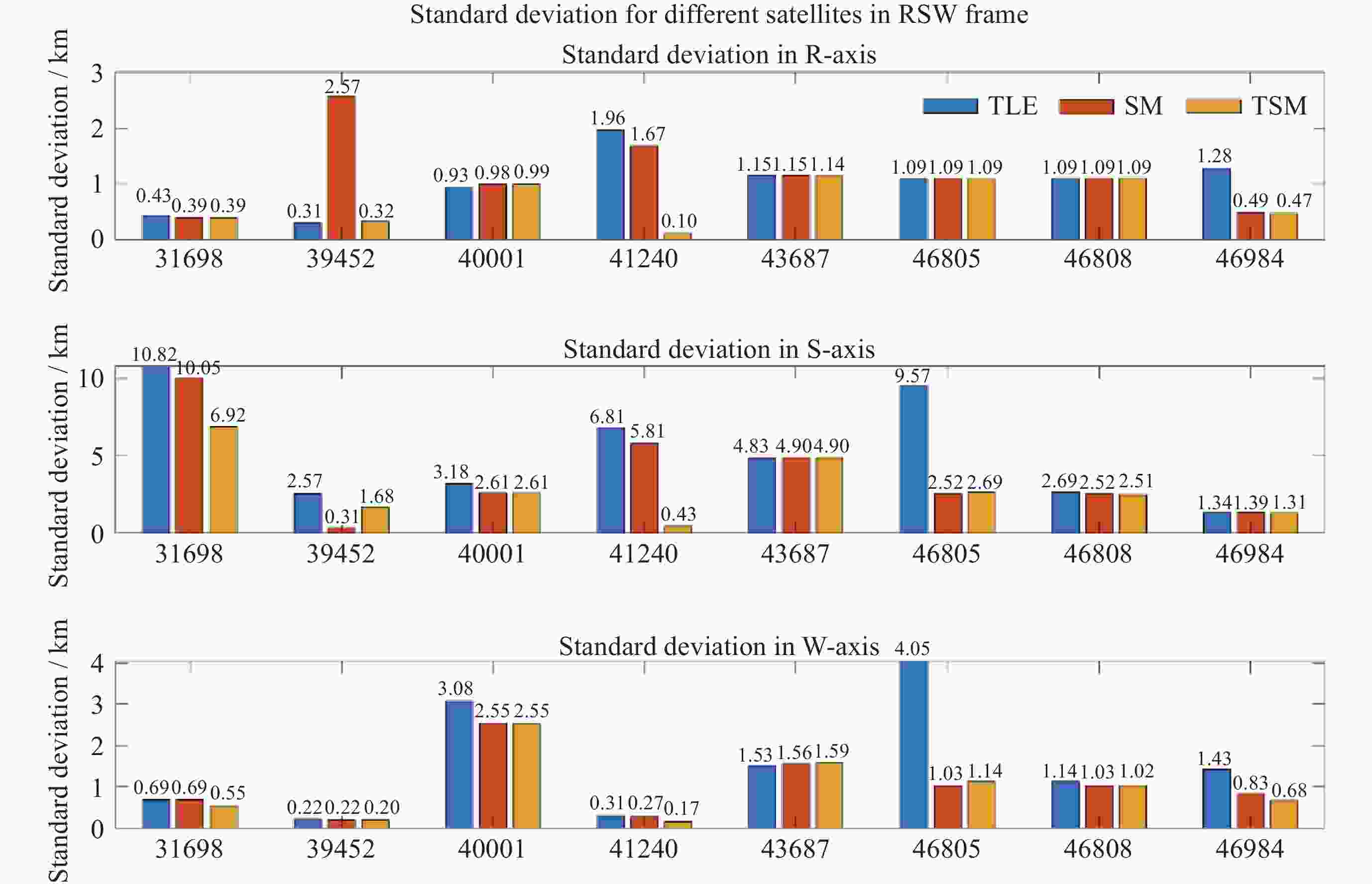
Table 4. RMSEs of the satellite orbit prediction
卫星ID 原始TLE SM/km TSM/km 相对精度提升/(%) 31698 10.852 10.084 6.951 28.87 39452 2.594 2.594 1.720 33.69 40001 4.527 3.783 3.778 0.11 41240 7.097 6.055 0.477 78.60 43687 5.196 4.826 4.657 3.25 46805 10.163 2.938 2.683 2.51 46808 3.114 2.938 2.925 0.42 46984 2.344 1.687 1.549 5.89
下载: 导出CSV
-
[1] KAZEMI S, AZAD N L, SCOTT K A, et al. Orbit determination for space situational awareness: a survey[J]. Acta Astronautica, 2024, 222: 272-295 doi: 10.1016/j.actaastro.2024.06.015 [2] VALLADO D A, CRAWFORD P. SGP4 orbit determination[C]//Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Honolulu: American Institute of Aeronautics and Astronautics, 2008 [3] 赵广宇, 桑吉章, 陈俊宇, 等. 利用稀疏角度数据改进空间目标TLE轨道预报精度[J]. 测绘地理信息, 2021, 46(S1): 301-304ZHAO Guangyu, SANG Jizhang, CHEN Junyu, et al. Improving the orbit prediction accuracy for NORAD objects using sparse angles data[J]. Journal of Geomatics, 2021, 46(S1): 301-304 [4] 陈俊宇, 林初森. 星链卫星TLE轨道预报精度分析和改善[J]. 昆明理工大学学报: 自然科学版, 2024, 49(5): 39-45CHEN Junyu, LIN Chusen. Analysis and improvement of TLE orbit prediction accuracy for starlink satellites[J]. Journal of Kunming University of Science and Technology:Natural Science, 2024, 49(5): 39-45 [5] 刘劲宏, 桑吉章, 刘宏康. 基于单纯形法的TLE轨道确定[J]. 空间科学学报, 2020, 40(6): 1102-1108 doi: 10.11728/cjss2020.06.1102LIU Jinghong, SANG Jizhang, LIU Hongkang. TLE orbital determination based on simplex method[J]. Chinese Journal of Space Science, 2020, 40(6): 1102-1108 doi: 10.11728/cjss2020.06.1102 [6] LIU J H, LONG W T, WU Y C, et al. TLE orbit determination using simplex method[J]. Geodesy and Geodynamics, 2023, 14(5): 438-455 doi: 10.1016/j.geog.2023.03.004 [7] 刘舒莳, 龚建村, 刘四清, 等. 基于经验正交分析法的暴时热层大气密度时空分布规律[J]. 地球物理学报, 2013, 56(10): 3236-3245LIU Shushi, GONG Jiancun, LIU Siqing, et al. Thermospheric density during geomagnetic storm based on EOF analysis[J]. Chinese Journal of Geophysics, 2013, 56(10): 3236-3245 [8] LIU J, WU C, LONG W, et al. Improving orbit prediction of the two-line element with orbit determination using a Hybrid algorithm of the Simplex Method and Genetic Algorithm[J]. Aerospace, 2025, 12(6): 527 doi: 10.3390/aerospace12060527 -
-
下载:
计量
- 文章访问数: 147
- HTML全文浏览量: 21
- PDF下载量: 8
-
被引次数:
0(来源:Crossref)
0(来源:其他)
